starting
sequencelengths 6
6
| target
int64 1
999
| closest
int64 1
999
| expression
stringlengths 1
38
| delta
int64 0
861
| score
int64 0
10
| size
int64 6
6
| __index_level_0__
int64 0
999k
|
|---|---|---|---|---|---|---|---|
[
75,
3,
25,
50,
5,
100
] | 198 | 198 | ((((100 - 5) + 75) + 3) + 25) | 0 | 10 | 6 | 487,900 |
[
100,
75,
6,
8,
1,
3
] | 582 | 582 | ((100 - 3) * 6) | 0 | 10 | 6 | 608,958 |
[
4,
10,
3,
10,
8,
9
] | 198 | 198 | (((3 * 4) + 10) * 9) | 0 | 10 | 6 | 607,498 |
[
100,
5,
6,
75,
25,
50
] | 353 | 354 | ((((100 / 25) + 50) + 5) * 6) | 1 | 9 | 6 | 787,423 |
[
10,
3,
5,
8,
3,
7
] | 506 | 507 | ((((8 * 7) - 5) * 10) - 3) | 1 | 9 | 6 | 893,450 |
[
2,
75,
5,
100,
50,
25
] | 551 | 550 | ((5 * 100) + 50) | 1 | 9 | 6 | 313,063 |
[
9,
7,
75,
25,
50,
100
] | 167 | 167 | (((((75 * 9) + 100) / 25) * 7) - 50) | 0 | 10 | 6 | 23,067 |
[
3,
10,
5,
50,
100,
25
] | 896 | 895 | ((((3 + 25) - 10) * 50) - 5) | 1 | 9 | 6 | 30,418 |
[
50,
75,
3,
25,
2,
100
] | 647 | 647 | (((((75 * 2) / 25) * 100) - 3) + 50) | 0 | 10 | 6 | 907,028 |
[
9,
10,
75,
100,
8,
6
] | 879 | 879 | (((6 + 100) * 9) - 75) | 0 | 10 | 6 | 798,175 |
[
3,
6,
9,
1,
10,
8
] | 679 | 679 | (((((8 + 3) * 6) + 1) * 10) + 9) | 0 | 10 | 6 | 317,894 |
[
7,
9,
7,
8,
1,
3
] | 833 | 833 | (((9 + 8) * 7) * 7) | 0 | 10 | 6 | 840,186 |
[
6,
1,
50,
25,
5,
75
] | 871 | 871 | (((((25 - 6) * 50) - 5) + 1) - 75) | 0 | 10 | 6 | 301,279 |
[
75,
100,
3,
50,
25,
6
] | 988 | 993 | ((((3 + 50) + 100) * 6) + 75) | 5 | 5 | 6 | 930,447 |
[
6,
3,
1,
5,
75,
50
] | 189 | 189 | ((((50 - 5) - 1) * 6) - 75) | 0 | 10 | 6 | 685,167 |
[
3,
25,
3,
9,
4,
7
] | 585 | 585 | ((((3 + 7) * 4) + 25) * 9) | 0 | 10 | 6 | 29,397 |
[
50,
7,
2,
8,
100,
25
] | 690 | 690 | (((100 * 7) - 8) - 2) | 0 | 10 | 6 | 317,926 |
[
25,
7,
100,
50,
6,
8
] | 4 | 4 | (100 / 25) | 0 | 10 | 6 | 779,268 |
[
8,
25,
100,
50,
75,
10
] | 97 | 97 | (100 - (75 / 25)) | 0 | 10 | 6 | 658,614 |
[
5,
10,
8,
9,
4,
75
] | 2 | 2 | (10 / 5) | 0 | 10 | 6 | 294,319 |
[
4,
9,
6,
8,
100,
7
] | 757 | 757 | (((100 + 9) * 7) - 6) | 0 | 10 | 6 | 322,659 |
[
1,
7,
10,
8,
2,
3
] | 975 | 974 | (((((8 - 1) * 7) * 10) - 3) * 2) | 1 | 9 | 6 | 366,522 |
[
1,
10,
7,
8,
10,
8
] | 928 | 928 | ((((8 + 10) * 7) - 10) * 8) | 0 | 10 | 6 | 145,719 |
[
10,
7,
5,
25,
8,
100
] | 481 | 481 | ((((5 * 10) + 7) * 8) + 25) | 0 | 10 | 6 | 794,210 |
[
50,
5,
1,
25,
3,
75
] | 344 | 344 | (((((75 + 50) * 3) - 5) - 25) - 1) | 0 | 10 | 6 | 827,200 |
[
10,
3,
8,
4,
25,
9
] | 176 | 176 | ((25 - 3) * 8) | 0 | 10 | 6 | 289,451 |
[
5,
7,
100,
75,
25,
7
] | 543 | 543 | (((7 * 75) - 7) + 25) | 0 | 10 | 6 | 896,435 |
[
2,
100,
4,
25,
7,
3
] | 819 | 819 | ((((4 * 100) - 3) * 2) + 25) | 0 | 10 | 6 | 916,354 |
[
3,
75,
10,
7,
100,
9
] | 474 | 474 | (((100 - (10 + 7)) + 75) * 3) | 0 | 10 | 6 | 323,826 |
[
7,
100,
8,
25,
1,
9
] | 257 | 257 | (((1 + 9) * 25) + 7) | 0 | 10 | 6 | 949,603 |
[
25,
3,
9,
75,
6,
50
] | 841 | 841 | (((((75 + 25) * 9) - 6) - 3) - 50) | 0 | 10 | 6 | 652,150 |
[
4,
5,
10,
9,
1,
6
] | 86 | 86 | ((10 * 9) - 4) | 0 | 10 | 6 | 868,645 |
[
25,
75,
7,
100,
5,
9
] | 602 | 602 | (((100 - 9) - 5) * 7) | 0 | 10 | 6 | 494,003 |
[
7,
5,
5,
3,
10,
25
] | 296 | 296 | ((((5 + 25) * 10) + 3) - 7) | 0 | 10 | 6 | 923,805 |
[
25,
50,
75,
10,
8,
100
] | 284 | 284 | (((((10 * 50) + 75) / 25) * 8) + 100) | 0 | 10 | 6 | 57,714 |
[
6,
100,
25,
5,
3,
75
] | 228 | 228 | (((75 + 6) - 5) * 3) | 0 | 10 | 6 | 383,168 |
[
2,
9,
5,
10,
3,
3
] | 184 | 184 | ((((10 - 3) * 9) * 3) - 5) | 0 | 10 | 6 | 601,223 |
[
6,
10,
9,
50,
4,
75
] | 57 | 57 | ((9 - (6 - 4)) + 50) | 0 | 10 | 6 | 103,492 |
[
75,
5,
100,
6,
10,
25
] | 642 | 642 | (((10 - (75 / 25)) + 100) * 6) | 0 | 10 | 6 | 118,243 |
[
6,
2,
7,
6,
1,
5
] | 478 | 478 | (((((6 + 1) * 7) * 5) - 6) * 2) | 0 | 10 | 6 | 549,505 |
[
75,
5,
6,
25,
50,
100
] | 625 | 625 | ((75 + 50) * 5) | 0 | 10 | 6 | 889,927 |
[
2,
3,
100,
9,
4,
8
] | 226 | 226 | (((9 + 100) + 4) * 2) | 0 | 10 | 6 | 11,690 |
[
4,
75,
4,
25,
50,
100
] | 126 | 126 | (((4 / 4) + 50) + 75) | 0 | 10 | 6 | 740,917 |
[
100,
50,
25,
8,
75,
5
] | 350 | 350 | ((50 * 5) + 100) | 0 | 10 | 6 | 588,932 |
[
75,
2,
100,
7,
4,
5
] | 148 | 148 | (((7 - 5) * 75) - 2) | 0 | 10 | 6 | 850,539 |
[
25,
6,
2,
7,
8,
100
] | 562 | 562 | ((((25 * 7) + 6) + 100) * 2) | 0 | 10 | 6 | 854,589 |
[
7,
2,
2,
1,
10,
10
] | 732 | 732 | (((((10 * 7) + 1) + 2) * 10) + 2) | 0 | 10 | 6 | 868,407 |
[
10,
1,
6,
7,
25,
7
] | 705 | 704 | (((((25 - 1) - 7) * 6) * 7) - 10) | 1 | 9 | 6 | 111,587 |
[
4,
6,
9,
10,
10,
2
] | 954 | 954 | (((10 * 10) + 6) * 9) | 0 | 10 | 6 | 38,207 |
[
100,
50,
4,
5,
75,
25
] | 962 | 960 | (((50 - (100 / (75 - 25))) * 4) * 5) | 2 | 8 | 6 | 869,054 |
[
75,
1,
6,
25,
8,
2
] | 959 | 959 | (((((75 - 1) + 8) * 6) * 2) - 25) | 0 | 10 | 6 | 936,536 |
[
100,
75,
7,
50,
5,
7
] | 338 | 338 | (((7 * 50) - 5) - 7) | 0 | 10 | 6 | 708,230 |
[
50,
100,
25,
75,
6,
1
] | 55 | 55 | ((50 - 1) + 6) | 0 | 10 | 6 | 419,363 |
[
5,
75,
7,
10,
3,
6
] | 679 | 679 | ((((75 - 7) * 10) + 5) - 6) | 0 | 10 | 6 | 947,352 |
[
2,
7,
10,
9,
5,
7
] | 531 | 531 | (((7 * 7) + 10) * 9) | 0 | 10 | 6 | 311,659 |
[
75,
100,
7,
4,
25,
2
] | 846 | 846 | ((((7 * 75) - 100) * 2) - 4) | 0 | 10 | 6 | 77,542 |
[
100,
4,
2,
9,
25,
2
] | 670 | 670 | (((((9 + 25) * 2) + 100) * 4) - 2) | 0 | 10 | 6 | 623,807 |
[
100,
1,
6,
25,
3,
1
] | 568 | 568 | ((((100 - 1) * 6) - 25) - 1) | 0 | 10 | 6 | 511,588 |
[
75,
9,
3,
7,
100,
50
] | 554 | 554 | (((75 - 3) * 7) + 50) | 0 | 10 | 6 | 448,636 |
[
75,
3,
8,
100,
50,
9
] | 779 | 779 | ((((100 - 9) - 3) * 8) + 75) | 0 | 10 | 6 | 14,088 |
[
5,
3,
9,
25,
50,
100
] | 939 | 940 | ((((25 - 3) * 9) * 5) - 50) | 1 | 9 | 6 | 456,747 |
[
7,
5,
4,
7,
10,
2
] | 521 | 521 | ((((7 * 10) + 5) * 7) - 4) | 0 | 10 | 6 | 101,200 |
[
3,
10,
75,
7,
100,
25
] | 90 | 90 | (100 - 10) | 0 | 10 | 6 | 957,696 |
[
4,
3,
3,
2,
9,
7
] | 450 | 450 | ((((3 * 7) + 4) * 2) * 9) | 0 | 10 | 6 | 980,916 |
[
50,
10,
75,
4,
1,
6
] | 989 | 989 | ((((4 * 6) + 75) * 10) - 1) | 0 | 10 | 6 | 695,733 |
[
9,
4,
8,
5,
10,
4
] | 468 | 468 | (((5 + 8) * 4) * 9) | 0 | 10 | 6 | 793,203 |
[
1,
10,
7,
4,
2,
6
] | 999 | 990 | (((((4 * 2) + 6) * 7) + 1) * 10) | 9 | 1 | 6 | 94,939 |
[
10,
8,
9,
10,
6,
5
] | 519 | 519 | ((((10 * 8) + 5) * 6) + 9) | 0 | 10 | 6 | 311,752 |
[
9,
3,
4,
10,
1,
2
] | 177 | 177 | (((2 * 9) * 10) - 3) | 0 | 10 | 6 | 538,091 |
[
4,
50,
10,
75,
25,
7
] | 99 | 99 | (((7 * 10) + 4) + 25) | 0 | 10 | 6 | 387,379 |
[
7,
50,
9,
5,
6,
75
] | 157 | 157 | (((75 - 50) * 6) + 7) | 0 | 10 | 6 | 851,460 |
[
50,
3,
100,
1,
75,
10
] | 639 | 640 | (((75 - 1) * 10) - 100) | 1 | 9 | 6 | 940,178 |
[
100,
50,
6,
25,
75,
3
] | 197 | 197 | (((100 - 3) + 75) + 25) | 0 | 10 | 6 | 827,613 |
[
6,
4,
75,
10,
2,
2
] | 664 | 664 | ((((2 + 75) + 6) * 2) * 4) | 0 | 10 | 6 | 278,555 |
[
75,
50,
1,
9,
100,
25
] | 909 | 909 | ((100 + 1) * 9) | 0 | 10 | 6 | 616,477 |
[
8,
7,
9,
2,
1,
5
] | 191 | 191 | ((((7 - 2) * 5) * 8) - 9) | 0 | 10 | 6 | 6,863 |
[
100,
25,
50,
5,
7,
3
] | 620 | 620 | ((((100 * 7) - 50) - 5) - 25) | 0 | 10 | 6 | 745,438 |
[
4,
100,
1,
25,
7,
75
] | 508 | 508 | ((((100 + 25) * 4) + 7) + 1) | 0 | 10 | 6 | 731,560 |
[
4,
3,
8,
100,
5,
2
] | 817 | 817 | ((((100 + 2) * 8) + 4) - 3) | 0 | 10 | 6 | 19,689 |
[
4,
5,
25,
50,
75,
5
] | 722 | 721 | ((((50 / 5) * 75) - 25) - 4) | 1 | 9 | 6 | 895,923 |
[
9,
2,
50,
7,
25,
100
] | 17 | 17 | ((25 + 9) / 2) | 0 | 10 | 6 | 524,623 |
[
8,
3,
75,
25,
10,
4
] | 982 | 982 | (((((25 - 4) - 8) * 75) + 10) - 3) | 0 | 10 | 6 | 929,537 |
[
25,
9,
100,
10,
50,
75
] | 832 | 833 | (((100 - ((75 / 25) + 10)) * 9) + 50) | 1 | 9 | 6 | 709,924 |
[
75,
25,
8,
50,
6,
100
] | 868 | 868 | (((((75 / 25) + 100) * 8) - 6) + 50) | 0 | 10 | 6 | 14,910 |
[
4,
9,
100,
5,
4,
75
] | 899 | 899 | (((9 * 100) - 5) + 4) | 0 | 10 | 6 | 117,895 |
[
3,
4,
7,
7,
9,
2
] | 44 | 44 | ((9 + 2) * 4) | 0 | 10 | 6 | 114,825 |
[
75,
50,
7,
100,
9,
6
] | 875 | 875 | ((75 + 50) * 7) | 0 | 10 | 6 | 518,258 |
[
100,
6,
2,
10,
8,
7
] | 638 | 638 | (((100 - 10) * 7) + 8) | 0 | 10 | 6 | 178,536 |
[
75,
9,
50,
8,
25,
7
] | 758 | 758 | ((((25 + 75) * 7) + 8) + 50) | 0 | 10 | 6 | 990,693 |
[
100,
5,
25,
50,
3,
75
] | 111 | 111 | ((((75 / 25) + 5) + 100) + 3) | 0 | 10 | 6 | 949,030 |
[
3,
100,
75,
50,
25,
1
] | 132 | 132 | ((((100 / 25) + 3) + 75) + 50) | 0 | 10 | 6 | 907,594 |
[
3,
2,
1,
9,
7,
6
] | 26 | 26 | ((9 * 3) - 1) | 0 | 10 | 6 | 207,323 |
[
25,
3,
8,
100,
75,
10
] | 27 | 27 | ((10 - 8) + 25) | 0 | 10 | 6 | 767,173 |
[
9,
50,
6,
7,
75,
10
] | 220 | 220 | (((6 + 7) + 9) * 10) | 0 | 10 | 6 | 106,497 |
[
4,
75,
100,
3,
25,
5
] | 540 | 540 | (((3 + 100) * 5) + 25) | 0 | 10 | 6 | 686,998 |
[
6,
7,
9,
10,
4,
5
] | 726 | 726 | ((((10 + 4) * 9) - 5) * 6) | 0 | 10 | 6 | 535,510 |
[
75,
8,
50,
10,
25,
8
] | 253 | 253 | ((((50 - 10) * 8) + 8) - 75) | 0 | 10 | 6 | 398,734 |
[
2,
9,
9,
75,
5,
25
] | 603 | 603 | ((((75 - 5) - 2) * 9) - 9) | 0 | 10 | 6 | 223,234 |
[
100,
5,
75,
5,
25,
4
] | 156 | 156 | ((((75 - 5) * 4) / 5) + 100) | 0 | 10 | 6 | 767,340 |
[
75,
100,
3,
8,
50,
5
] | 234 | 234 | (((75 - 5) + 8) * 3) | 0 | 10 | 6 | 21,348 |
Countdown Numbers Game Dataset
This dataset contains configurations and solutions for variations of the Countdown numbers game. Each example comprises a sequence of numbers, a target number, the computed solution (closest value), the arithmetic expression that achieves that value, the difference between the target and the computed value, and the final Countdown score.
HuggingFace Download Links
| Dataset Variant | Dataset Name | Download |
|---|---|---|
| Random | countdown-numbers-3-8 |
🤗 HuggingFace |
| Random Solvable | countdown-numbers-3-8-nz |
🤗 HuggingFace |
| Coundown Game Rules | countdown-numbers-6-gr |
🤗 HuggingFace |
Dataset Overview
Each data point in the dataset includes:
Numbers:
A sequence of $n$ integers $s_1, s_2, \ldots, s_n$ where $s_i \in {1, 2, \ldots, 100}$ for all $i \in {1, 2, \ldots, n}$, and $n \in {3, 4, \ldots, 8}$. (Note: In the traditional Countdown game, the numbers are subject to more specific restrictions.)Target:
An integer $t \in {1, 2, \ldots, 999}$. (For context, the standard Countdown game usually features targets from 101 and above.)Closest:
The value computed by a solver $r \in {1, 2, \ldots, 999}$ that is closest to the target number.Expression:
The arithmetic expression used to compute the closest value. For instance, $((2 + 48) \times 5) \div 10$Delta:
The absolute difference between the target and the closest value, i.e. $|t - r|$.Score:
The Countdown score calculated as $\max(0, 10 - |t - r|)$. This score reflects how close the computed value is to the target.
Dataset Variants
This dataset is provided in three variants:
Random:
Configurations and solutions generated by uniformly sampling and solving one million game instances, without additional restrictions.Random Solvable (Score > 0):
Configurations are generated by uniformly sampling numbers and then rejecting any sample that results in an unsolvable instance (i.e., a score of 0). This variant ensures that each instance has a solution that yields a positive score.Countdown:
Configurations generated by sampling 6 numbers in the style of the British TV show Countdown.
Score Distributions
The following histograms show the distribution of scores for each dataset variant:
Random Variant

Random Solvable (Score > 0) Variant

Countdown Game Rules

Generation Process
The dataset was created by:
- Uniformly sampling numbers within the specified ranges.
- Solving each sampled instance to determine the closest value, the corresponding expression, the difference from the target, and the score.
- For the Random Solvable (Score > 0) variant, rejection sampling was applied: instances that did not yield a positive score were discarded.
The train and test splits were created by randomly partitioning the instances into 80% training and 20% testing, using a stratified split based on the score and number of starting values.
Split Score/Size Distributions
The final distributions of scores and numbers are shown in the following histograms:
Random Variant
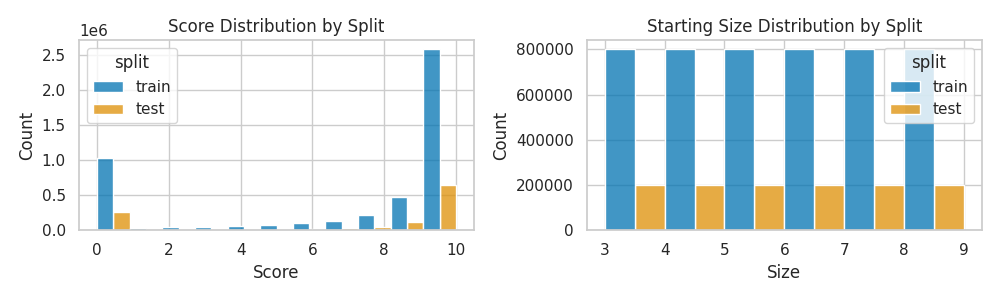
Random Solvable (Score > 0) Variant

Countdown Game Rules
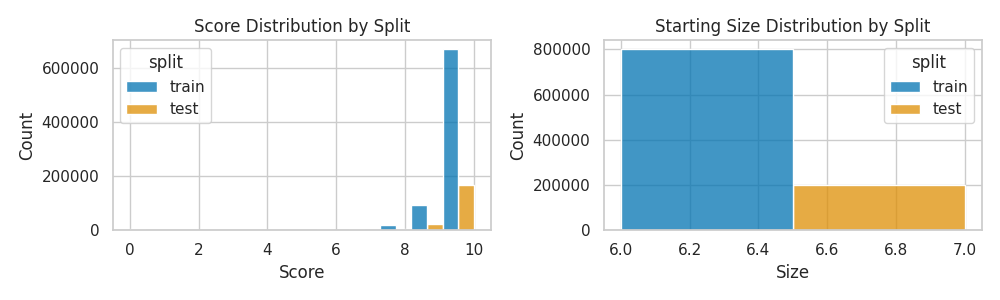
How to Use the Dataset
You can load and use this dataset with the Hugging Face datasets library. For example:
from datasets import load_dataset
dataset = load_dataset("alexjackson17/countdown-numbers-6-gr")
# Example: Access the first entry in the training split
example = dataset["train"][0]
print("Numbers: ", example["starting"])
print("Target: ", example["target"])
print("Closest: ", example["closest"])
print("Expression: ", example["expression"])
print("Difference: ", example["delta"])
print("Score: ", example["score"])
Citation
If you use this dataset in your research or projects, please cite it as follows:
@misc{jackson2025countdown,
title = {Countdown Numbers Game Dataset},
author = {Alex Jackson},
year = {2025},
note = {Released under the MIT License},
}
Funding Attribution
This work was supported by UK Research and Innovation [grant number EP/S023356/1], in the UKRI Centre for Doctoral Training in Safe and Trusted Artificial Intelligence (www.safeandtrustedai.org).
License
This dataset is released under the MIT License. See the LICENSE file for more information.
For questions, feedback, or further information, please contact Alex Jackson.
- Downloads last month
- 57