Datasets:

---

justus27

/

numina-1.5-numeric

like 0

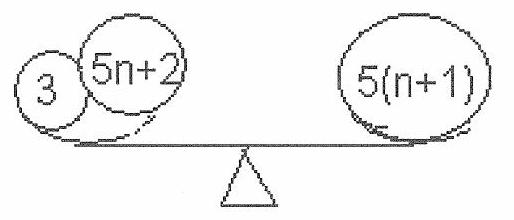
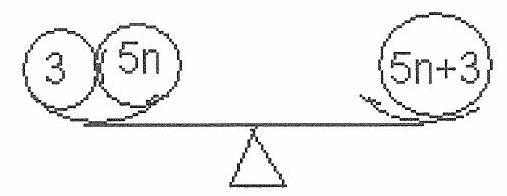
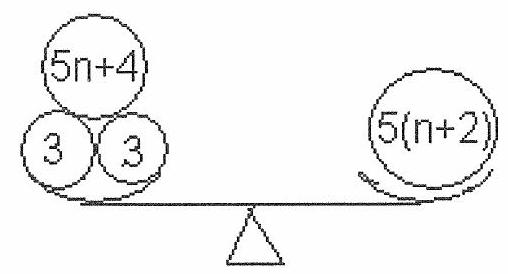
5. Kuzya the flea can make a jump in any direction on a plane for exactly 17 mm. Its task is to get from point $A$ to point $B$ on the plane, the distance between which is 1947 cm. What is the minimum number of jumps it must make to do this?

Answer: $\quad n_{\min }=1146$ jumps.

1146

Geometry

math-word-problem

Yes

Incomplete

olympiads

2. Integers, whose decimal notation reads the same from left to right and from right to left, we will call symmetric. For example, the number 513151315 is symmetric, while 513152315 is not. How many nine-digit symmetric numbers exist such that adding 11000 to them leaves them symmetric?

Answer: 8100 numbers of the form $\overline{a b c d 9 d c b a}$, where $a=1,2, \ldots, 9$, $b=0,1,2, \ldots, 9, c=0,1,2, \ldots, 9, d=0,1,2, \ldots, 8$.

8100

Number Theory

math-word-problem

Yes

Yes

olympiads

3. In city "N", there are 10 horizontal and 12 vertical streets, of which a pair of horizontal and a pair of vertical streets form the rectangular boundary of the city, while the rest divide it into blocks that are squares with a side length of 100 meters. Each block has an address consisting of two integers $(i ; j), i=1,2, . ., 9, j=1,2, \ldots, 11-$ the numbers of the streets that bound it from below and from the left. Taxis transport passengers from one block to another, adhering to the following rules: 1) pick-up and drop-off can be made at any point on the boundary of the block at the passenger's request; 2) it is forbidden to enter inside the block; 3) transportation is carried out along the shortest path; 4) a fee of 1 coin is charged for every 100 meters traveled (rounding the distance to the nearest 100 meters in favor of the driver). How many blocks are there in the city? What is the maximum and minimum fare that the driver can charge the passenger for a ride from block $(7,1)$ to block $(2 ; 10)$ without violating the rules?

Answer: 99 blocks; $c_{\min }=10$ coins, $c_{\max }=14$ coins.

99

Combinatorics

math-word-problem

Yes

Yes

olympiads

5. Kuzya the flea can make a jump in any direction on a plane for exactly 19 mm. Her task is to get from point $A$ to point $B$ on the plane, the distance between which is 1812 cm. What is the minimum number of jumps she must make to do this?

Answer: $n_{\min }=954$ jumps.

954

Geometry

math-word-problem

Yes

Yes

olympiads

Problem 3. Answer: 1) $\left\{\begin{array}{l}x=3 \\ y=3\end{array}\right.$ 2) $\left\{\begin{array}{l}x=-1 \\ y=7\end{array}\right.$

Solution Let's write down all the powers of the number 3 not exceeding $259: 1,3,9,27,81,243$. The difference between the number 259 and a power of three must be a power of two. $259-1=258, \quad 259-3=256=2^{8}, \quad 259-9=250, \quad 259-27=232, \quad 259-81=178, \quad 259-243=16=2^{4}$ Thus $$ \begin{aligned} & 2^{8}+3^{1}=259 \rightarrow x+5=8, y-2=1 \rightarrow\left\{\begin{array}{l} x=3 \\ y=3 \end{array}\right. \\ & 2^{4}+3^{5}=259 \rightarrow x+5=4, y-2=5 \rightarrow\left\{\begin{array}{l} x=-1 \\ y=7 \end{array}\right. \end{aligned} $$ Problem 4 Answer: 1) 4p 23kop 2) 152p 28kop Solution Let $x 522 y$ be the desired price in kopecks. This number must be divisible by 9, so $x+y=9 k, k \in Z$. Moreover, it must be divisible by 4, i.e., $2 y=4 \cdot m, m \in Z$. Possible options for the second condition: $y=0 ; 4 ; 8$ Case 1. $y=0$ $x=9 k \rightarrow x=9 \rightarrow \Sigma=952,20 \rightarrow a=26,45$ Case 2. $y=4$ $x+4=9 k \rightarrow x=5 \rightarrow \Sigma=552,24 \rightarrow a=15,34$ Case 3. $y=8$ $x+8=9 k \rightarrow x=1 \rightarrow \Sigma=152,28 \rightarrow a=4,23$ Considering the limit of $500 \mathrm{p}$, only case 3 is feasible. 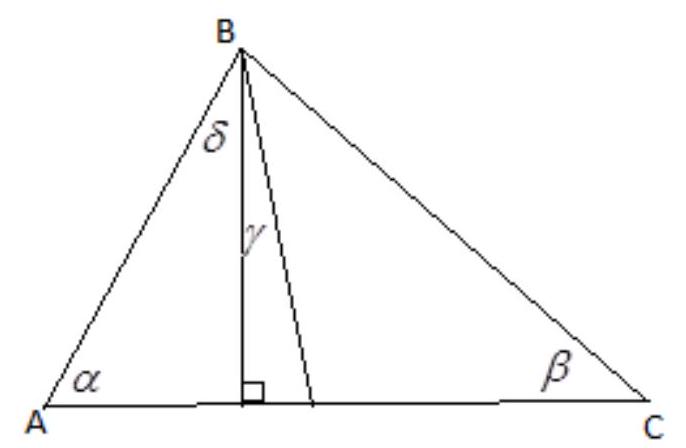Problem 5 Answer: $19^{\circ}$ Solution  $\delta=90^{\circ}-\alpha, \frac{180^{\circ}-\alpha-\beta}{2}=\delta+\gamma \rightarrow \gamma=\frac{180^{\circ}-\alpha-\beta}{2}-\left(90^{\circ}-\alpha\right)=\frac{\alpha-\beta}{2}$ In the case where $\alpha=75^{\circ}, \beta=37^{\circ}$, then $\gamma=\frac{75-37}{2}=19^{\circ}$

19

Algebra

math-word-problem

Incomplete

Yes

olympiads

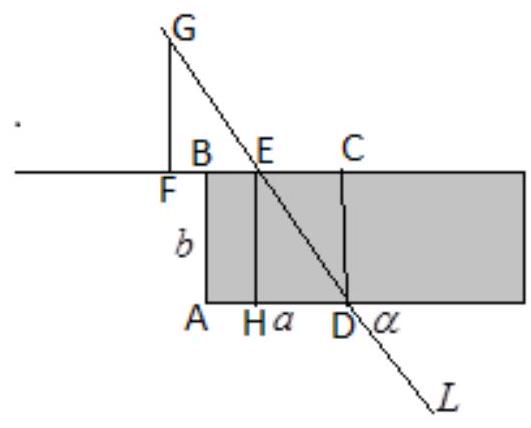
6. A plot of land in the form of a right-angled triangle with legs of 4 and 3 needs to be divided by a line $L$ into two plots such that 1) the plots have equal area; 2) the length of the common boundary (fence) of the plots is minimized. Indicate the points on the sides of the triangle through which the desired line $L$ passes and find the length of the fence.

Problem 6. Answer: 1) The line intersects the larger leg $B C$ (angle $\measuredangle C=90^{\circ}$) at point $M: B M=\sqrt{10}$ and the hypotenuse $B A$ at point $N: B N=\sqrt{10}$. 2) $L_{\text {min }}=2$

2

Geometry

math-word-problem

Yes

Yes

olympiads

1. When buying 2 shirts and 1 tie, the payment was 2600 rubles. Then the second purchase will have a $25 \%$ discount. The price of the $3-rd$ shirt is $1200 \cdot 0.75=900$ rubles. The total price of the entire purchase is $2600+900=3500$ rubles.

Answer: the purchase is possible, the total price is 3500 rubles.

3500

Algebra

math-word-problem

Incomplete

Yes

olympiads

1. When purchasing goods for an amount of no less than 1000 rubles, the store provides a discount on subsequent purchases of $50 \%$. Having 1200 rubles in her pocket, Dasha wanted to buy 4 kg of strawberries and 6 kg of sugar. In the store, strawberries were sold at a price of 300 rubles per kg, and sugar - at a price of 30 rubles per kg. Realizing that she didn't have enough money for the purchase, Dasha still managed to buy what she intended. How did she do it?

First purchase: 3 kg of strawberries, 4 kg of sugar. Its cost is $300 \times 3 + 4 \times 30 = 1020$ rubles. Second purchase: 1 kg of strawberries, 2 kg of sugar. With a $50\%$ discount, its price is $(300 + 60) \cdot 0.5 = 180$ rubles. The total amount of both purchases is $1200$ rubles.

1200

Logic and Puzzles

math-word-problem

Yes

Yes

olympiads

4. Petya wrote in the first column all five-digit numbers, in the notation of which digits from 0 to 7 are used, and in the second - the products of the digits of each such number. Vasya managed to calculate in his mind the sum of the numbers written in the second column. What result did he get

Answer: $28^{5}=17210368$.

17210368

Number Theory

math-word-problem

Yes

Problem not solved

olympiads

3. Let's show that the numbers $a(a+4)$ and $b(b+4)$ cannot be squares. Indeed, suppose, for example, $$ a(a+4)=c^{2}, c \in Z, c>0 $$ Rewrite this equation as $$ (a+2)^{2}-c^{2}=4 \quad \text { or } \quad(a+c+2)(a-c+2)=4 $$ Consider the left-hand side of this equation. Note that the smallest value of the first factor is 4. It is achieved when $a=1, c=1$. In this case, the second factor is 2, and the product of the factors is 8. Thus, we have shown that the left-hand side of the equation is greater than or equal to 8. This means that the equation has no solutions. There are four numbers $a b, a(b+4), b(a+4),(a+4)(b+4)$. Among the two numbers $a b, a(b+4)$, there can be no more than one square. Indeed, otherwise their product $a^{2} b(b+4)$ would also be a square, which means $b(b+4)$ is a square, which is impossible. For the same reasons, among the remaining pair of numbers $b(a+4),(a+4)(b+4)$, there can also be only one square. Thus, the six pairwise products contain no more than two squares of integers. For example, for $a=32$ and $b=4$, the numbers $b(a+4)=4 \cdot 36=144$ and $a(b+4)=32 \cdot 8=256$ are squares.

Answer: two squares, for example, when $a=32, b=4$.

2

Number Theory

proof

More than one problem

Yes

olympiads

1. The polynomial $p_{1}=x-a$ can have a root $x=a$ coinciding with one of the roots of the product $p(x)=p_{1}(x) \cdot p_{2}(x)$. Case $1 \quad a=1$ Then the polynomial $p_{2}(x)=(x-1)^{r}(x-2)^{s}(x+3)^{t}$, where $r \geq 1, s \geq 1, t \geq 1-$ are integers, $r+s+t=4$, satisfies the condition of the problem. The polynomial sum $p_{1}(x)+p_{2}(x)$ has a constant term $u=(-1)^{r+s} \cdot 2^{s} \cdot 3^{t}-1=(-1)^{t} \cdot 2^{s} \cdot 3^{t}-1$ which has a maximum value $u_{\max }=17$ when $r=1, s=1, t=2$. Case $2 \quad a=2$ Then the polynomial $p_{2}(x)=(x-1)^{r}(x-2)^{s}(x+3)^{t}$ and the polynomial $p_{1}(x)+p_{2}(x)$ has a constant term $u=(-1)^{r+s} \cdot 2^{s} \cdot 3^{t}-2=(-1)^{t} \cdot 2^{s} \cdot 3^{t}-2$, taking the maximum value $u_{\max }=16$ when $r=1, s=1, t=2$. Case $3 \quad a=-3$ The constant term $u=(-1)^{r+s} \cdot 2^{s} \cdot 3^{t}+3$ takes the maximum value $u_{\max }=21$ when $s=r=1, t=2$ The required polynomials: $p_{2}(x)=(x-1)(x-2)(x+3)^{2}, p_{1}(x)=x+3$

Answer: $p_{1}(x)=x+3, p_{2}(x)=(x-1)(x-2)(x+3)^{2} ; a_{0}=21$

21

Algebra

math-word-problem

Yes

Yes

olympiads

2. Answer: $\Sigma_{a}=1680$

Solution Let $a=p_{1}^{r_{1}} \cdot p_{2}^{r_{2}} \cdot \ldots \cdot p_{m}^{r_{m}}, b=p_{2}^{r_{2}} \cdot \ldots \cdot p_{m}^{r_{m}} \cdot$ Here $p_{k}$ are prime divisors, $r_{k}$ are their multiplicities. Let $q_{i}$ be any divisor of the number $b$. Then $q_{i}, p_{1} q_{i}, p_{1}^{2} q_{i}, \ldots, p_{1}^{r_{1}} q_{i}$ are divisors of the number $a$. Their sum $\sigma_{i}=q_{i}\left(1+p_{1}+p_{1}^{2}+\ldots+p_{1}^{r_{1}}\right)$. Then the sum of all divisors of the number $a$ is $\Sigma_{a}=\sum_{i} \sigma_{i}=\left(1+p_{1}+p_{1}^{2}+\ldots+p_{1}^{r_{1}}\right) \sum_{i} q_{i}=\left(1+p_{1}+p_{1}^{2}+\ldots+p_{1}^{r_{1}}\right) \Sigma_{b}$ Repeating the same for $\Sigma_{b}$, we get the formula for the sum of all divisors of the number $a$: $\Sigma_{a}=\left(1+p_{1}+p_{1}^{2}+\ldots+p_{1}^{r_{1}}\right) \cdot\left(1+p_{2}+p_{2}^{2}+\ldots+p_{2}^{r_{2}}\right) \cdot \ldots \cdot\left(1+p_{m}+p_{m}^{2}+\ldots+p_{m}^{r_{m}}\right)$ For the variant $1 a=540=2^{2} \cdot 3^{3} \cdot 5$ and $\Sigma_{a}=\left(1+2+2^{2}\right) \cdot\left(1+3+3^{2}+3^{3}\right) \cdot(1+5)=7 \cdot 40 \cdot 6=1680$

1680

Combinatorics

math-word-problem

Incomplete

Yes

olympiads

3. Answer: 1) 167 numbers; 2) $x_{\max }=975$

Solution According to condition 1) $5 x=6 k+3 \rightarrow\left\{\begin{array}{l}x=6 t-3 \\ k=5 t-3\end{array} \rightarrow 1 \leq 6 t-3 \leq 1000 \rightarrow t=1,2, \ldots, 167\right.$, i.e., 167 solutions. According to condition 2) $x=5 m, m>0, m \in Z \rightarrow$ GCD $(6 ; 25 m)=3 \rightarrow 25 m=6 k+3 \rightarrow\left\{\begin{array}{c}m=3 s \\ 25 s-2 k=1\end{array} \rightarrow\left\{\begin{array}{c}m=6 t+3 \\ \left\{\begin{array}{c}s=1+2 t \\ k=12+25 t\end{array}\right.\end{array}\right.\right.$ Then $x=30 t+15, t \geq 0, t \in Z$. Constraint: $1 \leq 30 t+15 \leq 1000 \rightarrow t=0,1,2, \ldots 32$. In total, 33 solutions, $x_{\max }=30 \cdot 32+15=975$

975

Number Theory

math-word-problem

Incomplete

Yes

olympiads

3. Answer: 1) 9 fractions; 2) $\left(\frac{p}{q}\right)_{\text {min }}=\frac{1}{5}$

Solution Transformation: $\frac{p-1}{q}<\frac{p}{q+1} \rightarrow(p-1)(q+1)<p q \rightarrow p-q<1$ For $q=1 \rightarrow 0<p<2 \rightarrow p=1$, i.e., there is only one fraction $\frac{p}{q}=\frac{1}{1}=1$, which does not satisfy the condition of the problem. For $q=2 \rightarrow 0<p<3 \rightarrow p=1 ; 2$, i.e., there is one fraction $\frac{p}{q}=\frac{1}{2}$, which satisfies the condition. For $q=3 \rightarrow 0<p<4 \rightarrow p=1 ; 2 ; 3$, i.e., there are two fractions $\frac{p}{q}=\frac{1}{3} ; \frac{2}{3}$, which satisfy the condition. For $q=4 \rightarrow 0<p<5 \rightarrow p=1 ; 2 ; 3 ; 4$, i.e., there are three fractions $\frac{p}{q}=\frac{1}{4} ; \frac{3}{4}$, which satisfy the condition. For $q=5 \rightarrow 0<p<6 \rightarrow p=1 ; 2 ; 3 ; 4 ; 5$, i.e., there are four fractions $\frac{p}{q}=\frac{1}{5} ; \frac{2}{5} ; \frac{3}{5} ; \frac{4}{5}$, which satisfy the condition. The total number of fractions is $1+2+2+4=9$. The smallest fraction $\left(\frac{p}{q}\right)_{\text {min }}=\frac{1}{5}$.

9

Number Theory

math-word-problem

More than one problem

Yes

olympiads

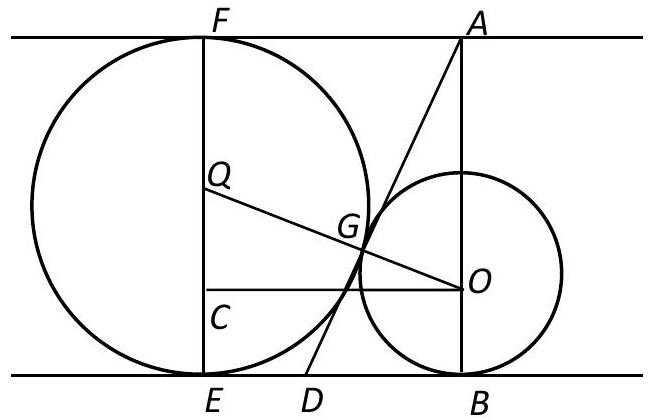
5. Let's introduce the following notations: $Q$ - the center of the first circle, $F, E, B$ - the points of tangency of the circles and lines, $G$ - the point of tangency of the circles, $AD$ - the common tangent (see the figure). Draw the line $OC$ parallel to the line $FA$. Let $FA=a, OG=r$. Then $AG=a \quad(AG=FA$ as tangents drawn from a point to the same circle are equal).  Since $QC=4-r, OQ=4+r, OA=8-r, OC=a$, from the right triangles $QOC$ and $AOG$ we get the system: $$ \left\{\begin{array}{c} (4-r)^{2}+a^{2}=(4+r)^{2} \\ r^{2}+a^{2}=(8-r)^{2} \end{array}\right. $$ Subtracting the first equation from the second, we get: $$ 4 \cdot(4-2r)=12 \cdot(4-2r) $$ From which it follows that $r=2$.

Answer: $r=2$. ## Variant №2

2

Geometry

math-word-problem

Incomplete

Yes

olympiads

3. A natural number $a$ is divisible by 21 and has 105 different divisors, including 1 and $a$. Find the smallest such $a$.

Answer: $a_{\min }=2^{6} \cdot 3^{4} \cdot 7^{2}=254016$

254016

Number Theory

math-word-problem

Yes

Yes

olympiads

3. A natural number $a$ is divisible by 35 and has 75 different divisors, including 1 and $a$. Find the smallest such $a$.

Answer: $a_{\text {min }}=2^{4} \cdot 5^{4} \cdot 7^{2}=490000$.

490000

Number Theory

math-word-problem

Yes

Yes

olympiads

1. A team of seven people is laying a 60 m pipe in the ground. To prepare the trench, they decided to dig in turns with the condition: each person digs for as long as the other six together would dig one-sixth of the trench. The 60 m trench was dug when the last member of the team had worked their allotted time. How many meters of the trench could they have dug in the same time if they all worked together?

Answer: $130 \mathrm{M}$.

130

Algebra

math-word-problem

Yes

Problem not solved

olympiads

3. A natural number $a$ is divisible by 55 and has 117 distinct divisors, including 1 and $a$. Find the smallest such $a$.

Answer: $a_{\min }=2^{12} \cdot 5^{2} \cdot 11^{2}=12390400$.

12390400

Number Theory

math-word-problem

Yes

Yes

olympiads

5. The border of a square with a side of 9, cut out of white cardboard, is painted red. It is necessary to cut the square into 6 equal-area parts, the boundaries of which contain segments painted red with the same total length. ## Solutions Option 1 Problem 1

Answer: 2 km. Solution $S-$ the length of the path, $S_{1}$ - the length of the path on descents, $S_{2}$ - the length of the path on ascents, $S / 2=S_{1}+S_{2}$ $t=15-8-6=1-$ the time of the journey there and back. Then $1=\frac{S_{1}}{6}+\frac{S_{2}}{3}+\frac{S}{2 \cdot 4}+\frac{S_{1}}{3}+\frac{S_{2}}{6}+\frac{S}{2 \cdot 4}=\left(\frac{1}{6}+\frac{1}{3}\right)\left(S_{1}+S_{2}\right)+\frac{S}{4}=\left(\frac{1}{6}+\frac{1}{3}\right) \frac{S}{2}+\frac{S}{4}=\frac{S}{2} \rightarrow S=2$ Problem 2 Answer: $\frac{1}{6}$ Solution. By the condition $\frac{p}{q}5 p$. Considering the naturality of $p$ and $q$, and the condition $p+q<8$ we have $6 p<p+q<8 \rightarrow p=1 \rightarrow q=6$ Problem 3 Answer: $a_{\min }=15876$ Solution Among the divisors of an even number divisible by 21 and being a square of an integer, there are $7^{2}, 3^{2}, 2^{2}$, i.e. $a=7^{2} \cdot 3^{2} \cdot 4 \cdot k^{2}$. Considering the five-digit nature, the inequality holds: $10000 \leq 7^{2} \cdot 3^{2} \cdot 4 \cdot k^{2} \leq 99998 \rightarrow 6 \leq k^{2} \leq 57 \rightarrow k_{\min }^{2}=9 \rightarrow a_{\min }=7^{2} \cdot 3^{2} \cdot 4 \cdot 9=15876$ Problem 4 Answer: $x=\frac{3}{2}$ Solution $x=\frac{4-[x]}{2} \rightarrow\{x\}=x-[x]=\frac{4-[x]}{2}-[x]=\frac{4-3[x]}{2}$ Since $0 \leq\{x\}<1 \rightarrow 0 \leq \frac{4-3[x]}{2}<1 \rightarrow \frac{2}{3}<[x] \leq \frac{4}{3}$ and the number $[x]-$ is an integer, the only valid value is $[x]=1$. 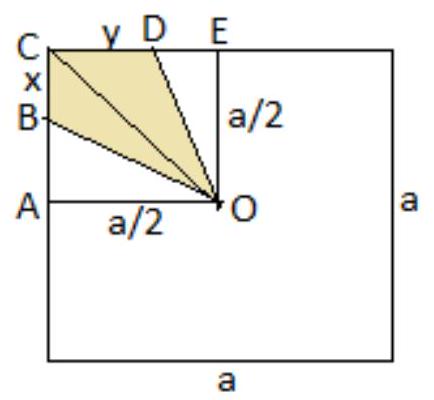Then $x=\frac{3}{2}$ Problem 5 Solution  O - the center of the square, the polygon $O B C D$ - one of the six desired pieces, $B C=x, C D=y, a=9$. $S_{\text {OBCD }}=\frac{a^{2}}{6}=\frac{a}{4} \cdot(x+y) \rightarrow x+y=\frac{2 a}{3}=6$ - the length of the red part of the boundary of the polygon. A way of cutting (one of ...)  Variant 2 Problem 1 Answer: 3 km. 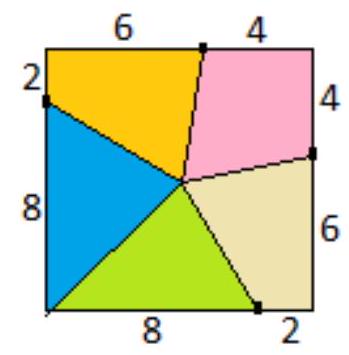Problem 2 Answer: $\frac{1}{4}$ Problem 3 Answer: $a_{\max }=5625$ Problem 4 Answer: $x=\frac{5}{2}$ Problem 5 Answer:  Variant 3 Problem 1 Answer: 1.5 km. 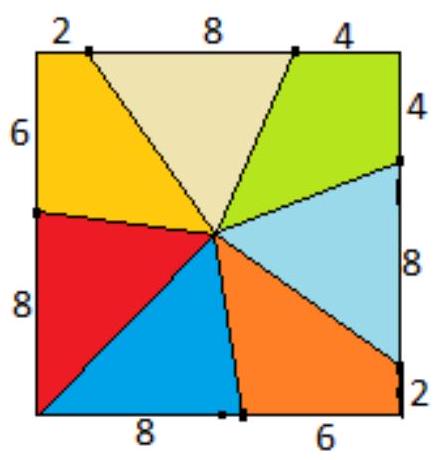Problem 2 Answer: $\frac{1}{4}, \frac{1}{5}$ Problem 3 Answer: $a_{\text {min }}=327184$ Problem 4 Answer: $x=-\frac{7}{2}$ Problem 5 Answer:  Variant 4 Problem 1 Answer: 1.4 km. Problem 2 Answer: $\frac{1}{6}, \frac{1}{7}$ Problem 3 Answer: $a_{\max }=74529$ Problem 4 Answer: $x=-\frac{3}{2}$ Problem 5 Answer: 

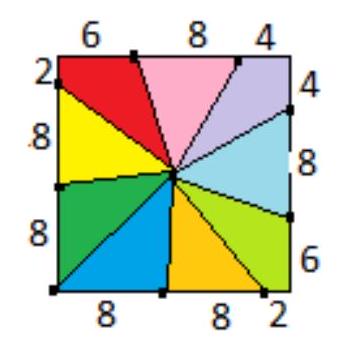6

Geometry

math-word-problem

Yes

Yes

olympiads

# 2.15. Final round of the "Rosatom" Olympiad, 8th grade

# 2.15. Final round of the "Rosatom" Olympiad, 8th grade ## Answers and solutions Problem 1 Answer: 1997 or 2011 The year of birth can be written as: $1000 x + 100 y + 10 z + u$. By the condition: $2013 - 1000x - 100y - 10z - u = z + u$. Case $1. x = 1 \rightarrow 2u = 1013 - 100y - 11z$ Estimate: $2u \leq 18, 11z \leq 99 \rightarrow 2u + 11z \leq 117 \rightarrow y = 9 \rightarrow$ $2u = 113 - 11z$. If $z \leq 8$, then $113 - 11z \geq 25$ and this is impossible, so $z = 9$. $2u = 113 - 99 = 14 \rightarrow u = 7$ and the year of birth is 1997. Case 2. $x = 2 \rightarrow 2u = 13 - 100y - 11z \rightarrow 100y = 13 - 11z - 2u \rightarrow y = 0$ $2u + 11z = 13 \rightarrow u = 1, z = 1$ and the year of birth is 2011. Problem 2 Answer: 84 $x$ - the number of tens, $y$ - the number of units. Case $1. x > y \quad 10x + y = 21(x - y) \rightarrow 11x = 22y \rightarrow x = 2y$ $y_{\max} = 4$, the largest number is 84 Case 2. $x < y \quad 10x + y = 21(y - x) \rightarrow 11y = 22x \rightarrow y = 2x$ $x_{\max} = 4$, the largest number is 84 Case 3. $x = y \quad 10x + y = 21(x - y) \rightarrow 10x + y = 0$ In digits, the last is impossible. Problem 3 Answer: 47 The original number is no more than two digits: $a = 10x + y$. $2 \cdot 1000 + (x - 2) \cdot 100 + (y - 7) \cdot 10 + 9 = (10x + y)^2 = 100x^2 + 20xy + y^2$. $(100x^2 + 20(y - 5)x + y^2 - 10y + 25) - 25 - 1800 + 61 = 0 \rightarrow$ $(10x + y - 5)^2 = 1764 = 42^2 \rightarrow 10x + y - 5 = 42 \rightarrow a = 47$ Problem 4 Answer: the second is larger. $\sqrt{2012} + \sqrt{2014} \vee 2\sqrt{2013} \rightarrow \sqrt{2014} - \sqrt{2013} \vee \sqrt{2013} - \sqrt{2012}$ $\frac{1}{\sqrt{2014} + \sqrt{2013}} \vee \frac{1}{\sqrt{2013} + \sqrt{2012}} \rightarrow \sqrt{2014} + \sqrt{2013} \wedge \sqrt{2013} + \sqrt{2012}$ $\sqrt{2014} > \sqrt{2012}$, i.e., the sign $\wedge$ corresponds to the sign $>$, and the opposite sign $\vee$ corresponds to the sign $<$. 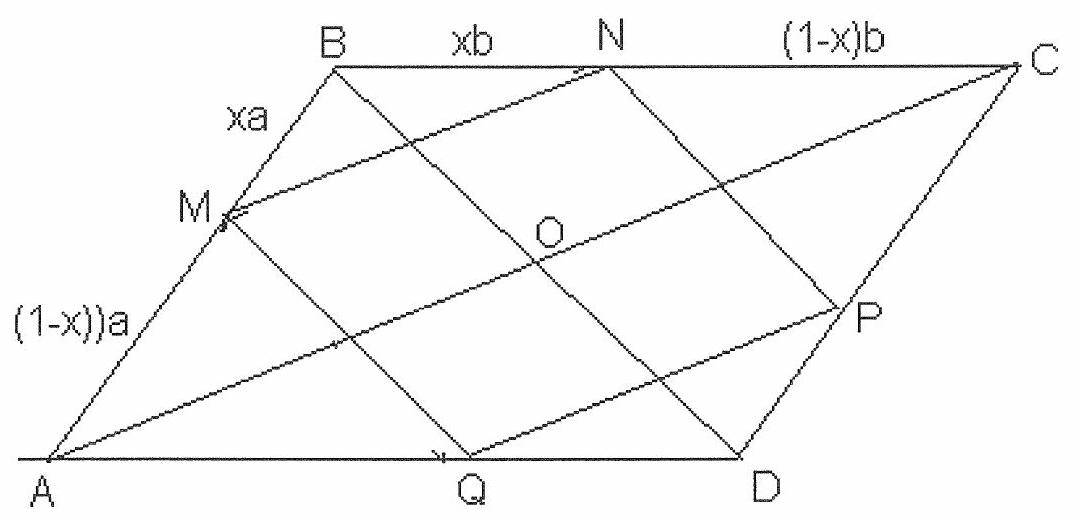Problem 5 Answer: $a = \frac{d \cdot D}{d + D} = \frac{2}{3}$  $AB = a, BC = b, x = BN : BC$ $\frac{NP}{d} = 1 - x \rightarrow NP = (1 - x)d$ $\frac{MN}{D} = x \rightarrow MN = xD$ $NP = MN \rightarrow (1 - x)d = xD \rightarrow x = \frac{d}{d + D} \rightarrow MN = \frac{dD}{d + D}$ In the variant $d = 1, D = 2$, so $MN = \frac{2}{3}$.

47

Other

math-word-problem

Incomplete

Yes

olympiads

Variant 1. $S_{1}=100, k_{1}=32, t_{1}=180, S_{2}=50, k_{2}=20, t_{2}=108, A=30$, $T=36$

Answer: 24 cows ## Problem 4 Solution. . $x=\frac{p}{q}$, options $p= \pm 1 ; \pm 5, q=1 ; 2 ; 4$ $4 p^{2}+a p q-5 q^{2}=0 \rightarrow a=\frac{5 q}{p}-4 \frac{p}{q}$ Case 1. $q=1 \rightarrow a=\frac{5}{p}-4 p \rightarrow a= \pm 1 ; \pm 8 ; \pm 19$ Case 2. $q=2 \rightarrow a=\frac{10}{p}-2 p \rightarrow a= \pm 8$ Case $3 . q=4 \rightarrow b=\frac{20}{p}-p \rightarrow b= \pm 1 ; \pm 19$

24

Algebra

math-word-problem

Incomplete

Yes

olympiads

# 2.3. Qualifying round of the "Rosatom" Olympiad, 11th grade ## Answers and solutions Problem 1 Answer 345

Solution Variant 1. $a_{1}=\log _{1+\sqrt{5}}(1+\sqrt{5})^{2}=2$ $a_{1} a_{2}+a_{1} a_{3}+a_{2} a_{3}=2(2+d)+2(2+2 d)+(2+d)(2+2 d)=2\left(d^{2}+6 d+6\right)$ Solving the equation $x=66 \rightarrow d^{2}+6 d-27=0 \rightarrow\left[\begin{array}{c}d=3 \\ d=-9\end{array} \rightarrow\right.$ increasing $\rightarrow d=3, a_{15}=2+14 \cdot 3=44, S_{15}=\frac{2+44}{2} \cdot 15=345$ Problem 2 Answer: $a=\pi n, \quad n=2 ; 3 ; \ldots 7$ Solution. Case 1. $\left\{\begin{array}{c}x+y=a \\ \sin x=\sin y\end{array} \rightarrow\left\{\begin{array}{c}x+y=a \\ {\left[\begin{array}{c}a) \quad y=x+2 \pi k \\ b) y=\pi-x+2 \pi m\end{array}\right.}\end{array}\right.\right.$ An infinite number of solutions can only be given by point $b$) when $a=\pi+2 \pi m$ under the condition that the line $x+y=a$ intersects the rectangle: vertices $(5 \pi ; 3 \pi)$ and $(2 \pi ;-\pi)$ lie on opposite sides of the line $x+y-\pi-2 \pi m=0 \leftrightarrow\left\{\begin{array}{c}7 \pi-2 \pi m>0 \\ -2 \pi m0 \\ \pi-2 \pi k0\end{array} \rightarrow a^{2}0\end{array} \rightarrow a^{2}>\frac{7}{4}-\right.\right.$ the condition for the solvability of the system. $\sqrt{16-a^{2}}=\frac{4 a^{2}+7}{4 a} \rightarrow 32 a^{4}-200 a^{2}+49=0 \rightarrow$ The second root $a^{2}=\frac{25+\sqrt{527}}{8} \approx 5.99$ satisfies the solvability condition, the first $a^{2}=\frac{25-\sqrt{527}}{8} \approx 0.25-$ does not. $s=4 a^{2}=\frac{25+\sqrt{527}}{2} \approx 23.98$

345

Other

math-word-problem

Incomplete

Yes

olympiads

3. Selection of solutions. $$ -\frac{7 \pi}{2} \leq \frac{2 \pi}{3}+2 \pi k \leq \pi \rightarrow-\frac{25}{12} \leq k \leq \frac{1}{6} \rightarrow k=-2 ;-1 ; 0 $$ $$ -\frac{7 \pi}{2} \leq \frac{\pi}{6}+2 \pi m \leq \pi \rightarrow-\frac{11}{6} \leq m \leq \frac{5}{12} \rightarrow m=-1 ; 0 $$ Problem 3 Answer: 1) $n_{\min }=3$ 2) total fund 39 thousand rubles 3) $x_{1}=20, x_{2}=10, x_{3}=5$, remainder 4 thousand rubles.

Solution. $x$ - the amount of money in the prize fund. 1st team. $\frac{x+1}{2}$ received, $x-\frac{x+1}{2}=\frac{x-1}{2}$ remaining. 2nd team. $\frac{x-1}{2}+\frac{1}{2}=\frac{x+1}{4}$ - received, $\frac{x-1}{2}-\frac{x+1}{4}=\frac{x-3}{4}$ - remaining 3rd team. $\frac{x-3}{8}+\frac{1}{2}=\frac{x+1}{8}$ - received, $\frac{x-3}{4}-\frac{x+1}{8}=\frac{x-7}{8}$ - remaining $n$-th team. $\frac{x+1}{2^{n}}$ - received, $\frac{x+1-2^{n}}{2^{n}}-$ remaining (induction) $\frac{x+1-2^{n}}{2^{n}}=p \rightarrow x=2^{n}(p+1)-1 \geq 37$ $(p+1) \geq \frac{38}{2^{n}} \rightarrow \frac{38}{2^{n}-1} \leq p \leq 4 \rightarrow 2^{n} \geq \frac{38}{5}=7.8 \rightarrow n_{\min }=3$ $\frac{38}{8}-1 \leq p \leq 4 \rightarrow 3.75 \leq p \leq 4 \rightarrow p=4$ 2) total fund 39 m.p. $x_{1}=20, x_{2}=10, x_{3}=5$

39

Algebra

math-word-problem

More than one problem

Yes

olympiads

Problem 4. Answer: $x=35$

Solution variant 1 The number $1600000000=2^{4} \cdot 2^{8} \cdot 5^{8}=2^{12} \cdot 5^{8}$ The product of numbers divisible by 5: $5 \cdot 10 \cdot 15 \cdot 20 \cdot 25 \cdot 30 \cdot 35=2^{4} \cdot 3^{2} \cdot 7 \cdot 5^{8}$, so for numbers $x<35$ $x$ ! does not divide 1600000000. The product of numbers divisible by 2: $2 \cdot 4 \cdot 6 \cdot 8 \cdot 10 \cdot 12 \cdot 14 \cdot 16=3^{2} \cdot 5 \cdot 7 \cdot 2^{15}$, i.e., for numbers $x \geq 15$ the number $x$ ! divides $2^{12}$. Thus, 35 ! divides $5^{8}$ and $2^{12}$, i.e., 1600000000. 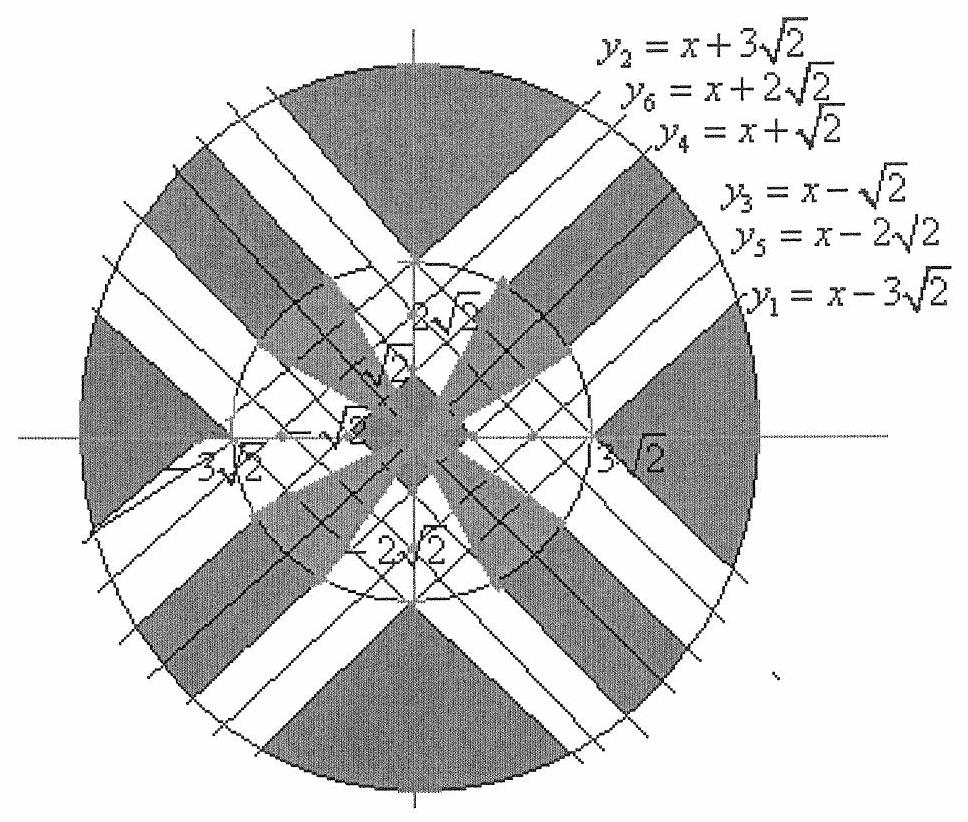Problem 5 Answer: $\alpha \in\left(\frac{\pi}{4}-\arcsin \frac{1}{3 \sqrt{2}}+\frac{\pi k}{2} ; \frac{\pi}{4}+\arcsin \frac{1}{3 \sqrt{2}}+\frac{\pi k}{2}\right), k \in Z$ Solution,  The white stripes correspond to points in the plane whose distance to one of the lines $\left[\begin{array}{l}x+y= \pm 2 \sqrt{2} \\ x-y= \pm 2 \sqrt{2}\end{array}\right.$ does not exceed 1. If the center $\left\{\begin{array}{l}x=3 \sqrt{2} \cos \alpha, \\ y=3 \sqrt{2} \sin \alpha\end{array}\right.$ is $(x-3 \sqrt{2} \cos \alpha)^{2}+(y-3 \sqrt{2} \sin \alpha)^{2}=1$ in the gray zone, then the system has no solutions. (Green sectors by $\alpha$). The boundaries of the sectors:

35

Algebra

math-word-problem

Incomplete

Yes

olympiads

# 2.8. Final round of the "Rosatom" Olympiad, 7th grade ## Answers and solutions 1 Answer: 5

Solution. $x(x+2)+1=x^{2}+2 x+1=(x+1)^{2}=36 \rightarrow x+1=6 \rightarrow x=5$. 2 Answer: $a=0,-1,-2,-3$ Solution. The coefficient $2 a+3 \neq 0$ for integer $a$, so the equation has a unique solution for all integer $a$. This solution is $x=\frac{4 a+9}{2 a+3}=\frac{2(2 a+3)+3}{2 a+3}=2+\frac{3}{2 a+3}$. The integer value of $x$ is possible in the following cases: 1) $2 a+3=-1$; 2) $2 a+3=1$; 3) $2 a+3=-3$; 4) $2 a+3=3$. Case 1) gives $a=-2$, case 2) gives $a=-1$, case 3) gives $a=-3$, case 4) gives $a=0$. 3 Answer: 16 Solution. Factorize the number 86400 into prime factors: $86400=2^{7} \cdot 3^{3} \cdot 5^{2}$. If $p, q$ and $r$ are different prime numbers thought of by Petya, Masha, and Vova respectively, $A$ is the number announced by the grandmother, and the game continued for 3 rounds, then the last number heard by Vova is $A \cdot p^{3} \cdot q^{3} \cdot r^{2}$. Comparing it with $2^{7} \cdot 3^{3} \cdot 5^{2}$, we conclude that $r=5, A$ does not contain 3 and 5 as its divisors, Petya and Masha thought of the numbers 2 and 3, and the grandmother announced the number $2^{4}=16$. 4 Answer: $a=2$ Solution. Case 1. $a>0$ The solution to the first inequality is $x \leq \frac{2}{a}$, the solution to the second inequality is $x \geq-\frac{a}{2}$. The solution to the system is the interval $\left[-\frac{a}{2} ; \frac{2}{a}\right]$, the length of which is $\frac{2}{a}+\frac{a}{2}=2 \rightarrow \frac{(a-2)^{2}}{2 a}=0 \rightarrow a=2$. Case 2. $a=0$ The first inequality is satisfied for all $x$, the second inequality is satisfied for $x \geq 0$. The solution to the system is a half-line, not an interval. Case 3. $a<0$ The solution to the first inequality is $x \geq \frac{2}{a}$, the solution to the second inequality is $-x \geq-\frac{a}{2}$. The solution to the system is the half-line $x \geq-\frac{a}{2}$, not an interval.

2

Algebra

math-word-problem

Incomplete

Yes

olympiads

5. Answer: into $(n-2)$ triangles.

Solution. Let the best dissection contain $m$ triangles. We will show that this number can be reduced by at least 1 if there is a triangle among them, all vertices of which are inside the polygon (Fig. 1)  Fig. 1 The highlighted triangle can be "collapsed into a point," suggesting a new way of dissection with fewer triangles. Therefore, the best dissection does not contain such triangles. We will show that the number $m$ can be reduced if among the triangles there is one with two vertices inside the polygon (Fig. 2)  Fig. 2 By "collapsing" the two points $A$ and $B$ into one, a dissection method with fewer triangles can be obtained. Therefore, in the best dissection method, there cannot be more than one vertex of the triangles inside the polygon. We will show that if there is one vertex, then in the best dissection, the other vertices of the triangles must coincide with the vertices of the polygon (Fig. 3)  Fig. 3 By moving points $B$ and $C$ to the vertices of the polygon, the number of triangles in the dissection can be reduced. Therefore, if there is one vertex of the triangles inside the polygon, the best dissection contains $n$ triangles (Fig. 4)  Fig. 4 Finally, the case where none of the vertices of the triangles are inside the polygon, and all others must be at the vertices of the polygon, leads to a dissection along rays emanating from one vertex (it doesn't matter which one!) (Fig. 5)  Fig. 5 Such a dissection contains $(n-2)$ triangles. In variant 1, $n=90$, so the minimum number of triangles is 88.

88

Geometry

math-word-problem

Incomplete

Yes

olympiads

2.13. Final round of the "Rosatom" Olympiad, 9th grade # Answers and solutions ## Problem 1 Answer: 2 $5-x, 9-2 x, 9-x-$ modified side lengths, $05\end{array}\right.$ Problem 2 Answer: 1) $a=-8, b=9$ 2) $4 x^{2}-x+3$ $16 x^{4}+a x^{3}+25 x^{2}-6 x+b=\left(4 x^{2}+A x+B\right)^{2}=$ $=16 x^{4}+A^{2} x^{2}+B^{2}+8 A x^{3}+8 B x^{2}+2 A B x=$ $=16 x^{4}+8 A x^{3}+\left(A^{2}+8 B\right) x^{2}+2 A B x+B^{2}$ $8 A=a, A^{2}+8 B=25,2 A B=-6, B^{2}=b$ $A^{3}+8 A B=25 A \rightarrow A^{3}-25 A-24=0 \rightarrow\left[\begin{array}{c}A=-1 \\ A^{2}-A-24=0 \rightarrow \text { no integers }\end{array}\right.$ $B=3, a=-8, b=9$ Problem 3 Answer: 1) $a_{15}=44, d=3$ 2) $a_{15}=-44, d=-3$ $S_{n}^{2}=\frac{n\left(6 n^{2}+3 n-1\right)}{2} \rightarrow S_{n+1}^{2}-S_{n}^{2}=(3 n+2)^{2}=a_{n+1}^{2} \rightarrow a_{n+1}=\left[\begin{array}{c}3 n+2 \rightarrow d=3 \\ -3 n-2 \rightarrow d=-3\end{array}\right.$ $a_{15}=\left[\begin{array}{c}44 \\ -44\end{array}\right.$ Problem 4 Answer: $a=2 n-3, n \in Z, n \geq 1$ $a=|x|+x-3=\left\{\begin{array}{c}2 x-3, x \geq 0 \\ -3, x<0\end{array}\right.$ The equation $2 x-3=a$ has a unique solution for $x \geq 0$. It is the only one. Problem 5 Answer: 1) 1) $2: 9$, 2) $2: 3$

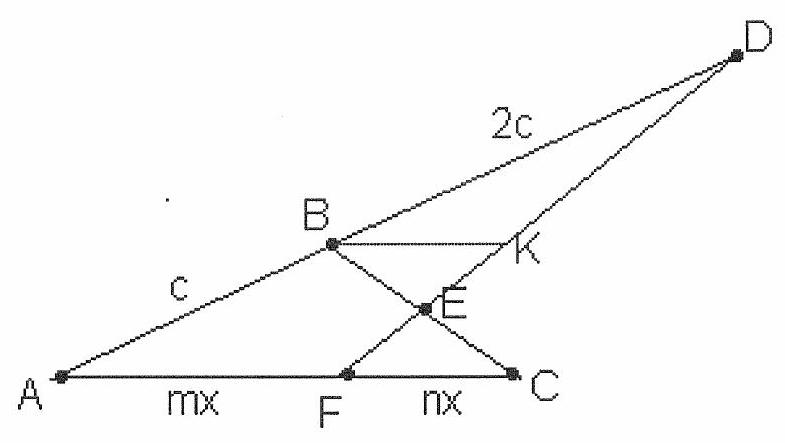
Solution. Case 1. The location of point $D$ is indicated in the figure.  Line $B K$ is parallel to $A C \rightarrow \frac{B K}{m x}=\frac{2 c}{3 c} \rightarrow B K=\frac{2 m x}{3}$ From the similarity of $\triangle B K E$ and $\triangle C F E \rightarrow \frac{B K}{n x}=\frac{B E}{E C} \rightarrow \frac{B E}{E C}=\frac{2 m}{3 n}$ In the problem, $m=1, n=3 \rightarrow B E: E C=2: 9$ Case 2. The location of point $D$ is indicated in the figure.  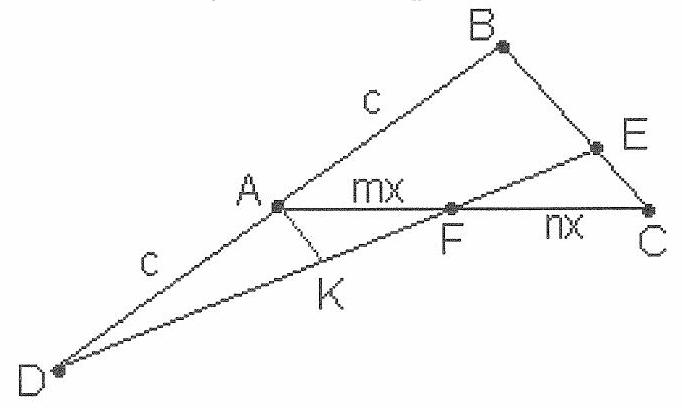Line $A K$ is parallel to $B C$, from the similarity of $\triangle D A K$ and $\triangle D B E \rightarrow A K=\frac{B E}{2}$ From the similarity of $\triangle A F K$ and $\triangle C F E \rightarrow \frac{A K}{E C}=\frac{m}{n} \rightarrow B E: E C=2 m: n$ $B E: E C=2: 3$

2

Algebra

math-word-problem

More than one problem

Yes

olympiads

1. Answer: 1) 4 people read books, went fishing, but did not collect mushrooms 2) 17

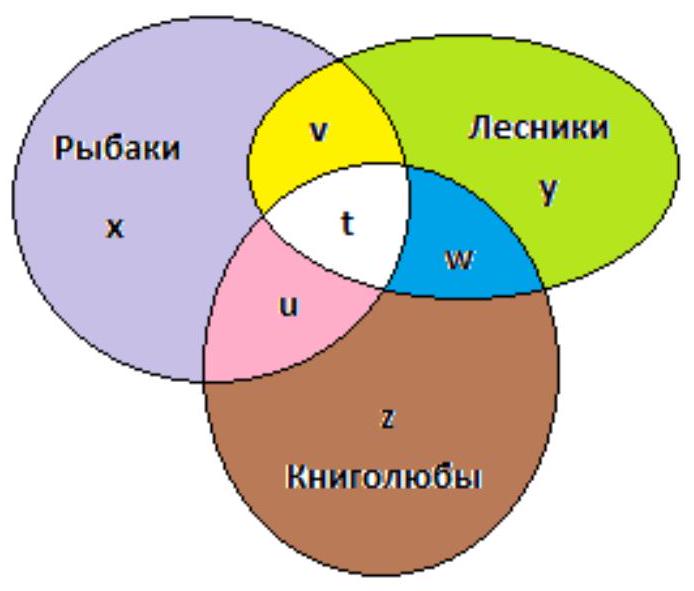
Solution. The diagram shows the distribution of children by interests:  The letters $x, y, z, u, v, w, t$ represent the number of schoolchildren engaged in one of the activities. For example, the letter $v$ represents the number of fishermen who collect mushrooms but do not read books. The conditions of the problem: $$ \left\{\begin{array}{c} x+y+z+u+v+w+t=57 \\ x+u+v+t=25 \\ y+v+w+t=26 \\ z+u+w+t=27 \\ w+t=9 \\ v+t=8 \end{array}\right. $$ Transformation: $\left\{\begin{array}{c}x+u=17 \\ y+v=17 \\ z+u=18 \\ w=9-t \\ v=8-t \geq 0 \rightarrow 0 \leq t \leq 8\end{array} \rightarrow\left\{\begin{array}{c}x=17-u \\ y=9+t \\ z=18-u \\ w=9-t \\ v=8-t \geq 0 \rightarrow 0 \leq t \leq 8\end{array}\right.\right.$ Substitution of $x, y, z, v, w$ into the first equation of the system $17-u+9+t+18-u+u+8-t+9-t+t=57 \rightarrow 61-u=57 \rightarrow u=4$. 

4

Combinatorics

math-word-problem

Incomplete

Yes

olympiads

2.17. Final round of the "Rosatom" Olympiad, 7th grade # Answers and solutions Problem 1 Answer: 9 There exists a set of 8 buttons in which there are no three buttons of the same color: each color has two buttons. In any set of 9 buttons, there will be at least one triplet of buttons of the same color. If we assume the opposite, that there are no more than 2 buttons of the same color, then there can be no more than 8 such buttons in total, which contradicts the condition.

Answer: 9 buttons. Problem 2 Answer: 1261 \[ \left\{\begin{array}{l} a=35 n+1 \\ a=45 m+1 \end{array} \rightarrow 35 n=45 m \rightarrow 7 n=9 m \rightarrow\left\{\begin{array}{c} n=9 t \\ m=7 t, t \in Z \end{array} \rightarrow\right.\right. \] \[ a=315 t+1 \geq 1000 \rightarrow t \geq 4 \rightarrow a_{\text {min }}=1261 \] ## Problem 3 Answer: 1) 4026 2) Sasha At each step of the game, the sum of the numbers written on the cards in the bag does not change. At the beginning of the game, it was \(2013 \times 2=4026\). Each step of the game changes the parity of the number of cards in the bag, as it reduces their number by one. Initially, the total number of cards in the bag is odd, so Sasha will make his move when the number of cards in the bag is odd, and Dasha when it is even. The last move occurs when there is one card in the bag, i.e., their number is odd, and Sasha will notice this. Problem 4 Answer: 1) \(17 \quad\) 2) 90 \((12,18,21,24,27,30,36,42,45,48,54,60,63,72,81,84,90)\) \(x, y\) - digits of the desired number \[ a=10 x+y=3 k, \quad a=10 x+y=(x+y) m \rightarrow\left\{\begin{array}{c} x+y=\frac{3 k}{m}, 2 \leq m \leq 10, \\ 10 x+y=3 k, 4 \leq k \leq 33 \end{array}\right. \] \[ \left\{\begin{array}{l} x=\frac{k}{3} \cdot \frac{m-1}{m} \\ y=\frac{k}{3} \cdot \frac{10-m}{m} \end{array}\right. \] Case \(m=2 \rightarrow\left\{\begin{array}{l} x=k / 6 \\ y=4 k / 3 \end{array} \rightarrow k=6 t \rightarrow\left\{\begin{array}{l} x=t \\ y=8 t \end{array} \rightarrow t=1 \rightarrow a=18\right.\right. \] Case \(m=3 \rightarrow\left\{\begin{array}{l} x=2 k / 9 \\ y=7 k / 9 \end{array} \rightarrow k=9 t \rightarrow\left\{\begin{array}{l} x=2 t \\ y=7 t \end{array} \rightarrow a=27\right.\right. \] Case \(m=4 \rightarrow\left\{\begin{array}{l} x=k / 4 \\ y=k / 2 \end{array} \rightarrow k=4 t \rightarrow\left\{\begin{array}{l} x=t \\ y=2 t \end{array} \rightarrow a=12,24,36,48\right.\right. \] Case \(m=5 \rightarrow\left\{\begin{array}{c} x=4 k / 15 \\ y=k / 3 \end{array} \rightarrow k=15 t \rightarrow\left\{\begin{array}{l} x=4 t \\ y=5 t \end{array} \rightarrow a=45\right.\right. \] Case \(m=6 \rightarrow\left\{\begin{array}{l} x=5 k / 18 \\ y=2 k / 9 \end{array} \rightarrow k=18 t \rightarrow\left\{\begin{array}{l} x=5 t \\ y=4 t \end{array} \rightarrow a=54\right.\right. \] Case \(m=7 \rightarrow\left\{\begin{array}{l} x=2 k / 7 \\ y=k / 7 \end{array} \rightarrow k=7 t \rightarrow\left\{\begin{array}{l} x=2 t \\ y=t \end{array} \rightarrow a=21,42,63,84\right.\right. \] Case \(m=8 \rightarrow\left\{\begin{array}{c} x=7 k / 24 \\ y=k / 12 \end{array} \rightarrow k=24 t \rightarrow\left\{\begin{array}{l} x=7 t \\ y=2 t \end{array} \rightarrow a=72\right.\right. \] Case \(m=9 \rightarrow\left\{\begin{array}{c} x=8 k / 27 \\ y=k / 27 \end{array} \rightarrow k=27 t \rightarrow\left\{\begin{array}{c} x=8 t \\ y=t \end{array} \rightarrow a=81\right.\right. \] Case \(m=10 \rightarrow\left\{\begin{array}{c} x=3 k / 10 \\ y=0 \end{array} \rightarrow k=10 t \rightarrow\left\{\begin{array}{l} x=3 t \\ y=0 \end{array} \rightarrow a=30,60,90\right.\right. 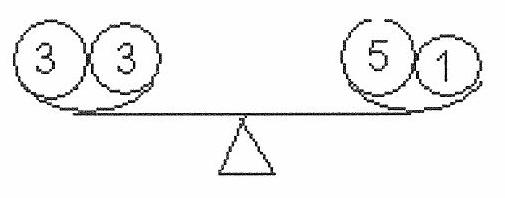\] \[ a_{\max }=90, \text{ number of numbers } 17 \] Problem 5 Answer: 2 weights Indicate the minimum number of 3 kg weights needed to weigh loads of 1, 2, 3, and 4 kg. 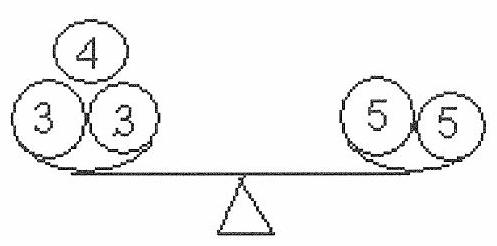Load of 1 kg - 2 weights of 3 kg are needed  Load of 2 kg or 3 kg - 1 weight of 3 kg is needed  Load of 4 kg - 2 weights of 3 kg are needed  The weight of any load when divided by 5 has a remainder of 0, 1, 2, 3, or 4. If the remainder is 0, the load can be weighed using only 5 kg weights. 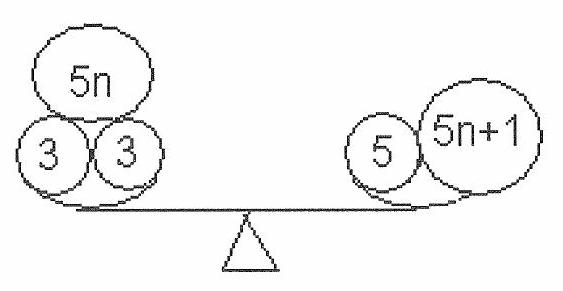If the weight of the load is \(5 n+1\), the weighing picture is obtained from the picture of weighing 1 kg:  If the weight of the load is \(5 n+2\), the weighing picture can be used for a 2 kg load:  If the weight of the load is \(5 n+3\), the weighing picture can be used for a 3 kg load:  Finally, a load of \(5 n+4\) kg is weighed similarly to a 4 kg load: 

1261

Combinatorics

math-word-problem

Yes

Yes

olympiads

4. The borrower and the lender agreed that an interest-free loan of 1365 t.r. would be repaid monthly, on the last day of the month. In the first month, a certain amount (an integer number of t. r.) is returned, and in each subsequent month, the amount returned is 1 t.r. more than in the previous month. For what maximum number of months could such a loan be issued, and how much did the borrower pay in the first month?

4. The Law of Cosines: \[ \begin{aligned} & B C^{2}=A B^{2}+A C^{2}-A B \cdot A C=a(a+c)+(a+c)^{2}-(a+c) \sqrt{a(a+c)}= \\ & =(a+c)(2 a+c-\sqrt{a(a+c)}) \end{aligned} \] ## Variant 2 Problem 1 Answer: 17

17

Algebra

math-word-problem

Yes

Incomplete

olympiads

3. In the decimal representation of a six-digit number $a$, there are no zeros and the sum of its digits is 18. Find the sum of all different numbers obtained from the number $a$ by cyclic permutations of its digits. In a cyclic permutation, all digits of the number, except the last one, are shifted one place to the right, and the last one is moved to the first place.

3. Solution. Case 1. The number $a=333333$. This number does not change under cyclic permutations, so it is the only one and the sum of the numbers is the number itself, that is, 333333. Case 2. The number $a$ consists of three identical cycles of two digits each, for example, $a=242424$. Such numbers have two different cyclic permutations: 242424 and 424242, the sum of which is $666666=2 \cdot 333333$. For any other such number, we will get the same sum of its cyclic permutations: $151515+515151=666666$ and so on. Case 3. The number $a$ consists of two identical cycles of three digits each, for example, $a=423423$. Such numbers have three different cyclic permutations: 423423, 342342, and 234234, the sum of which is $999999=3 \cdot 333333$. For any other such number, we will get the same sum of its cyclic permutations: $513513+351351+135135=999999$ and so on. Case 4. All six cyclic permutations are different. Let $a=a_{5} \cdot 10^{5}+a_{4} \cdot 10^{4}+a_{3} \cdot 10^{3}+a_{2} \cdot 10^{2}+a_{1} \cdot 10+a_{0}$. If we write out all its cyclic permutations in the same form, add the results, and regroup the terms, we get $a_{5}\left(10^{5}+10^{4}+\ldots+1\right)+a_{4}\left(10^{5}+10^{4}+\ldots+1\right)+\ldots+a_{0}\left(10^{5}+10^{4}+\ldots+1\right)=$ $=\left(a_{5}+a_{4}+a_{3}+a_{2}+a_{1}+a_{0}\right)\left(10^{5}+10^{4}+\ldots+1\right)=18 \cdot 111111=1999998$

1999998

Number Theory

math-word-problem

Yes

Yes

olympiads

5. On a sheet of paper, 14 parallel lines $L$ and 15 lines $P$ perpendicular to them are drawn. The distances between adjacent lines from $L$ from the first to the last are given: 2;4;6;2;4;6;2;4;6;2;4;6;2. The distances between adjacent lines from $P$ are also known: 3;1;2;6;3;1;2;6;3;1;2;6;3;1. Find the greatest length of the side of a square whose boundaries lie on the lines $L$ and $P$.

5. Solution. We will prove that the maximum length of the side of the square is 40. Calculate the distance from the first to the last line in $P: 3+1+2+6+3+1+2+6+3+1+2+6+3+1=40$. Therefore, the side length of the square cannot be more than 40. On the other hand, in $L$ the distance from the second line to the third line from the end is $4+6+2+4+6+2+4+6+2+4=40$. This means that a square with a side length of 40 exists.

40

Geometry

math-word-problem

Yes

Yes

olympiads

1. Pete and Vasya invited their classmates to their birthday at Pete's house and seated everyone at a round table to drink tea. Pete noted for himself the smallest number of chairs separating him from each of the invited guests, except for Vasya. By adding up these numbers, he got 75. Find the number of chairs at the table, given that it is even. What is the smallest number of chairs that separated Pete and Vasya?

Answer: 20 chairs, 6 chairs.

20

Combinatorics

math-word-problem

Yes

Yes

olympiads

1. Pete and Vasya invited their classmates to their birthday at Pete's house and seated everyone at a round table to drink tea. Pete noted for himself the smallest number of chairs separating him from each of the invited guests, except for Vasya. By adding these numbers, he got 95. Find the number of chairs at the table, given that it is even. What is the smallest number of chairs that separated Pete and Vasya?

Answer: 22 chairs, 5 stools.

22

Combinatorics

math-word-problem

Yes

Problem not solved

olympiads

1. Pete and Vasya invited their classmates to their birthday at Pete's house and seated everyone at a round table to drink tea. Pete noted for himself the smallest number of chairs separating him from each of the invited guests, except for Vasya. By adding up these numbers, he got 114. Find the number of chairs at the table, given that it is even. What is the smallest number of chairs that separated Pete and Vasya?

Answer: 24 chairs, 7 chairs.

24

Combinatorics

math-word-problem

Yes

Yes

olympiads

1. The polynomial $P(x)$ with integer coefficients satisfies the condition $P(29)=P(37)=2022$. Find the smallest possible value of $P(0)>0$ under these conditions.

Answer: $P(0)_{\min }=949$.

949

Algebra

math-word-problem

Yes

Yes

olympiads

1. The polynomial $P(x)$ with integer coefficients satisfies the condition $P(11)=P(13)=2021$. Find the smallest possible value of $P(0)>0$ under these conditions.

Answer: $P(0)_{\text {min }}=19$.

19

Algebra

math-word-problem

Yes

Yes

olympiads

1. The polynomial $P(x)$ with integer coefficients satisfies the condition $P(19)=P(21)=2020$. Find the smallest possible value of $P(0)>0$ under these conditions.

Answer: $P(0)_{\min }=25$.

25

Algebra

math-word-problem

Yes

Yes

olympiads

3. Answer: $C_{12}^{3}=220$

Solution Let the number be represented using $k$ threes and $m$ fours, $m+k=12, m \geq 1, k \geq 1$ Then, by the divisibility rule for 9, the sum of the digits of the number must be divisible by 9: $\left\{\begin{array}{c}3 k+4 m=9 t \\ m+k=12, m \geq 1, k \geq 1\end{array}\right.$. Notice that from the first equation $m=3 s$, and from the second $k=3 u$, so $\left\{\begin{array}{c}3 u+4 s=3 t \\ s+u=4, s \geq 1, u \geq 1\end{array} \rightarrow\left\{\begin{array}{c}s=3 v \rightarrow u+4 v=t \\ s=3, u=1, v=1, t=5\end{array}\right.\right.$ Thus, in the representation of the desired numbers, there are 3 threes and 9 fours. We need to place the 3 threes in different ways on the available 12 positions, and the remaining places will be occupied by fours. The number of such combinations is $C_{12}^{3}=220$.

220

Combinatorics

math-word-problem

Incomplete

Yes

olympiads

1. Answer: $f_{\max }=6$

Solution $z=27-x-y \rightarrow f=\log _{3} x+\log _{3} y+\log _{3}(27-x-y)$  Fig 1 The figure shows the location of points $a$ and $b$, giving the maximum value of $f$ at $x=x^{*}, y=y^{*}, z^{*}=27-x^{*}-y^{*}$. If the position of point $a$ is changed while keeping point $b$ unchanged, then the function $f\left(x, y^{*}\right)$ has a maximum at $x=x^{*}$, so $f^{\prime}\left(x, y^{*}\right)=\left.\frac{1}{\ln 3}\left(\frac{1}{x}-\frac{1}{27-x-y^{*}}\right)\right|_{x=x^{*}}=0 \rightarrow \frac{1}{x^{*}}-\frac{1}{27-x^{*}-y^{*}}=0$ Similarly, by fixing the position of point $a$ and changing the position of point $b$, we find that the function $f\left(x^{*}, y\right)$ has a maximum at $y=y^{*}$ and its derivative at this point is zero. $$ f^{\prime}\left(x^{*}, y\right)=\left.\frac{1}{\ln 3}\left(\frac{1}{y}-\frac{1}{27-x^{*}-y}\right)\right|_{y=y^{*}}=0 \rightarrow \frac{1}{y^{*}}-\frac{1}{27-x^{*}-y^{*}}=0 $$ Solving the system together, we find that $x^{*}=y^{*}=z^{*}=9$ and $f_{\max }=3 \log _{3} 9=6$

6

Inequalities

math-word-problem

Incomplete

Yes

olympiads

2. The number $A$ in decimal form is represented as $A=\overline{7 a 631 b}$, where $a, b$ are non-zero digits. The number $B$ is obtained by summing all distinct six-digit numbers, including $A$, that are formed by cyclic permutations of the digits of $A$ (the first digit moves to the second position, the second to the third, and so on, with the last digit moving to the first position). How many numbers $A$ exist such that $B$ is divisible by 121? Find the largest such $A$.

2. Solution. The sum of the digits of number $A$ and the numbers obtained from $A$ by cyclic permutations of its digits is $a+b+17$. After summing these numbers (there are 6 of them), in each digit place of number $B$ we get $a+b+17$, so $B=(a+b+17)\left(10^{5}+10^{4}+10^{3}+10^{2}+10+1\right)=(a+b+17) \cdot 111111$. Since $111111=3 \cdot 7 \cdot 11 \cdot 13 \cdot 37$, $B$ is divisible by 121 if and only if $a+b+17$ is divisible by 11. Since $a$ and $b$ are digits, there are only two possible cases: $a+b=5$ and $a+b=16$. From this, we find the possible pairs of $a$ and $b$: $a=1, b=4 ; a=2, b=3 ; a=3, b=2 ; a=4, b=1 ; a=7, b=9 ; a=8, b=8 ; a=9, b=7$. Thus, 7 numbers satisfy the condition of the problem. The largest number is obtained when $a=9, b=7$. It is 796317.

796317

Number Theory

math-word-problem

Yes

Yes

olympiads

4. Answer: $a_{\min }=15876$

Solution. The number $a=m^{2}$ can only be divisible by 21 if $m$ is divisible by 3 and 7, i.e., $m=21k \rightarrow a=441k^{2}$. From the fact that it is a five-digit number, it follows that $10000 \leq 441k^{2} \leq 99999 \rightarrow 23 \leq k^{2} \leq 226$. The smallest even $k=6$ and $a_{\min}=441 \cdot 36=15876$ Problem 5 Answer: 1) 16 2) possibly, in an infinite number of ways. Solution. The triangle $MNP$ is shown in the figure.  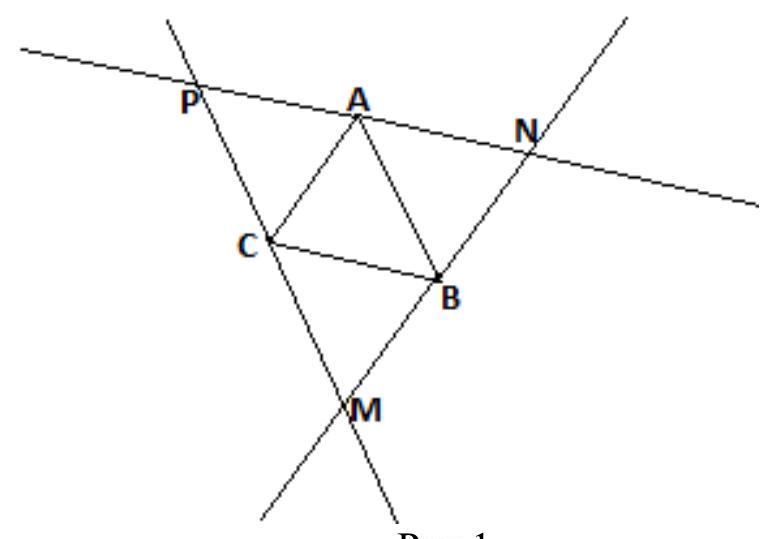Fig. 1 Construction: Through point $A$, draw a line $L_{A}$ parallel to $BC$, through point $B$ - a line $L_{B}$ parallel to $AC$, and through point $C$ - a line $L_{C}$ parallel to $AB$. The constructed lines intersect pairwise at points $M$, $N$, and $P$. Quadrilaterals $ACMB$ and $ACBN$ are parallelograms (by construction), $MB=CA=BN$, i.e., $B$ is the midpoint of side $MN$. Similarly, for the other sides. Triangle $MNP$ is similar to triangle $ABC$ with a similarity coefficient $k=2$, so its area is 4 times the area of triangle $ABC$, i.e., $S_{MNP}=16$. To answer the second question of the problem, we will indicate the locus of points on the plane from which the given segment $AB$ is seen at the given angle $\gamma$. Such a locus is an arc of a circle for which the segment $AB$ is a chord subtending an arc with a central angle $2\gamma$. The construction of such an arc is shown in Fig. 2  Fig. 2 Construction: 1) Construct segment $BK$ at an angle $\gamma$ to segment $AB$, point $K$ lies on the perpendicular bisector of segment $AB$ 2) Through point $B$, draw a perpendicular $BO$ to segment $BK$, point $O$ lies on the perpendicular bisector of segment $AB$ 3) Construct a circle with center at point $O$ and radius equal to the length of segment $BO$; 4) From any point $M$ on arc $ACB$ (and its symmetric arc $ADM$), segment $AB$ is seen at an angle $\gamma$. Proof. $BK$ is a tangent to the circle, so the arc between the tangent and chord $AB$ is measured by the central angle $2\gamma$, and the inscribed angle $AMB$ is half of this arc, i.e., $\gamma$. Construction of triangle $MNP$, similar to $\triangle ABC$:  1) Circle $K$ is circumscribed around $\triangle ABC$. Circle $K'$ is symmetric to circle $K$ with respect to line $AB$. On the arc of circle $K'$ with chord $AB$, from which segment $AB$ is seen at an angle $\gamma=\measuredangle ACB$, choose any point $P$ such that the sides of angle $APB$ are not parallel to $AC$ and $BC$, and point $C$ is inside angle $APB$. 2) Through point $C$, draw a line such that it forms an angle $\beta=\measuredangle ABC$ with one of the sides of angle $APB$. Denote the points of intersection of this line with the sides of angle $APB$ as $M$ and $N$. 3) Triangle $MNP$ is similar to $\triangle ABC$ by two angles. Points $A$, $B$, and $C$ lie on the sides of triangle $MNP$ and are not their midpoints.

15876

Number Theory

math-word-problem

Not a problem

Yes

olympiads

1. Each athlete participating in the marathon can be categorized into at least one of three categories: cheerful, trained, or beginners. It is known that every sixteenth cheerful athlete is a beginner, and one-fifth of the beginners are cheerful. One-fifth of the trained athletes are cheerful, and only one-tenth of the cheerful athletes are trained. Finally, one-fifth of the beginners are trained, and one-eighth of the trained athletes are beginners. Only three participants in the marathon are trained, cheerful beginners simultaneously. How many athletes started the race if they were given no more than 150 numbers?

Answer: 130 athletes.

130

Combinatorics

math-word-problem

Yes

Incomplete

olympiads

3. The real numbers $x_{1}, x_{2}$, and $x_{3}$ are the three roots of the equation $x^{3}-3 x^{2}+2(1-p) x+4=0$, considering their possible multiplicities. Find the smallest value of the expression $\left(x_{1}-1\right)^{2}+\left(x_{2}-1\right)^{2}+\left(x_{3}-1\right)^{2}$ under these conditions. For which $p$ is it realized?

The smallest value 6 is achieved when $p=1$.

6

Algebra

math-word-problem

Yes

Yes

olympiads

5. How many different pairs of integers $a$ and $b$ exist such that the equation $a x^{2}+b x+1944=0$ has positive integer roots?

Answer: $\quad 108+24=132$ pairs.

132

Algebra

math-word-problem

Yes

Yes

olympiads

5. How many different pairs of integers $a$ and $b$ exist such that the equation $a x^{2}+b x+432=0$ has positive integer roots

Answer: $\quad 78+20=98$ pairs.

98

Algebra

math-word-problem

Yes

Yes

olympiads

1. By the condition $$ T(t)=\frac{270-s(t)}{s(t) / t}=\frac{t(270-s(t))}{s(t)}=C>1, t \in[0.5 ; 1] $$ Then $s(t)=\frac{270 t}{t+C}$ on this interval. The speed of movement $$ \begin{aligned} & v(t)=s^{\prime}(t)=\frac{270 C}{(t+C)^{2}}=60 \text { when } t=1 \text {, i.e. } \\ & \qquad 2 c^{2}-5 c+2=0 \rightarrow C_{1}=2, C_{2}=\frac{1}{2} \end{aligned} $$ The second value of the constant is not allowed by the condition. Thus, $s(t)=\frac{270 t}{t+2}$ and $s(1)=90$. $$ v(t)=\left.\frac{540}{(t+2)^{2}}\right|_{t=\frac{1}{2}}=\frac{432}{5}=86.4 \text { km } / \text { hour } $$

Answer: 1) 90 km; 2) 86.4 km/hour

90

Algebra

math-word-problem

Yes

Yes

olympiads

3. If $m+2019 n$ and $n+2019 m$ are divisible by $d$, then the number $$ 2019(m+2019 n)-(n+2019 m)=(2019^2-1) n $$ is also divisible by $d$. If $n$ is divisible by $d$, and $m+2019 n$ is divisible by $d$, then $m$ is divisible by $d$ and the numbers $m$ and $n$ are not coprime. Therefore, $d$ divides the number $$ 2019^2-1=2018 \cdot 2020=2^3 \cdot 5 \cdot 101 \cdot 1009 $$ Thus, the smallest possible prime number is $d=101$. It remains to find coprime $m$ and $n$ for which it is realized. For example, $m=102, n=1$. Then $$ \begin{gathered} m+2019 n=102+2019=2121=21 \cdot 101 \text { and } \\ n+2019 m=1+2019 \cdot 102=205939=2039 \cdot 101 . \end{gathered} $$

Answer: $d_{\text {min }}=101$.

101

Number Theory

math-word-problem

Yes

Yes

olympiads

1. Kostya is making a car trip from point A to point B, which are 320 km apart. The route of the trip is displayed on the computer screen. At any moment in time $t$ (hours), Kostya can receive information about the distance traveled $s(t)$ (km), the speed of movement $v(t)$ (km/hour), and the estimated time $T=T(t)$ (hours) until the end of the trip. The program for calculating $T(t)$ is based on the assumption that the remaining part of the journey will be traveled at a speed equal to the average speed of the vehicle's movement over the time interval $[0 ; t]$. One hour after the start of the trip, he looked at the speedometer - 60 km/h. On the time interval $[1 ; 2]$, Kostya noticed that $T>1$ and does not change. How far from point $A$ was the car two hours after the start of the trip? What was the speed of the car 2 hours after the start of the trip?

Answer: 1) 128 km; 2) 38.4 km/h.

128

Algebra

math-word-problem

Yes

Yes

olympiads

3. It is known that for some positive coprime numbers $m$ and $n$, the numbers $m+2024 n$ and $n+2024 m$ have a common prime divisor $d>7$. Find the smallest possible value of the number $d$ under these conditions.

Answer: $d_{\min }=17$. For example, $$ \begin{aligned} & m=16, n=1 \rightarrow 2024 m+n=2024 \cdot 16+1=32385=17 \cdot 1905 \\ & m+2024 n=16+2024=17 \cdot 120 \end{aligned} $$

17

Number Theory

math-word-problem

Yes

Yes

olympiads

1. Vasya is making a car trip from point A to point B, which are 360 km apart. The route of the trip is displayed on the computer screen. At any moment in time $t$ (hours), Vasya can receive information about the distance traveled $s(t)$ (km), the speed of movement $v(t)$ (km/hour), and the estimated time $T=T(t)$ (hours) until the end of the trip. The program for calculating $T(t)$ is based on the assumption that the remaining part of the journey will be traveled at a speed equal to the average speed of the vehicle's movement over the time interval $[0 ; t]$. On the time interval $[0.5 ; 1.5]$, Vasya noticed that $T>1$ and does not change. An hour after the start of the trip, he looked at the speedometer - 80 km/hour. How far from point $A$ was the car at that moment? What was the speed of the car 30 minutes after the start of the trip?

Answer: 1) 120 km; 2) 115.2 km/h.

120

Algebra

math-word-problem

Yes

Yes

olympiads

3. It is known that for some positive coprime numbers $m$ and $n$, the numbers $m+1941 n$ and $n+1941 m$ have a common prime divisor $d>8$. Find the smallest possible value of the number $d$ under these conditions.

Answer: $d_{\min }=97$. For example, $$ \begin{aligned} & m=96, n=1 \rightarrow 1941 m+n=1941 \cdot 96+1=97 \cdot 1921 \\ & m+1941 n=96+1941=97 \cdot 21 \end{aligned} $$

97

Number Theory

math-word-problem

Yes

Yes

olympiads

1. Danya is making a car trip from point A to point B, which are 300 km apart. The route of the trip is displayed on the computer screen. At any moment in time $t$ (hours), Danya can receive information about the distance traveled $s(t)$ (km), the speed of movement $v(t)$ (km/hour), and the estimated time $T=T(t)$ (hours) until the end of the trip. The program for calculating $T(t)$ is based on the assumption that the remaining part of the journey will be traveled at a speed equal to the average speed of the vehicle's movement over the time interval $[0 ; t]$. One hour after the start of the trip, he looked at the speedometer - 75 km/h. On the time interval $[1 ; 1.5]$, Danya noticed that $T$ did not change. How far from point $A$ was the car 90 minutes after the start of the trip, and what was its speed?

Answer: 1) 180 km; 2) 48 km/h.

180

Algebra

math-word-problem

Yes

Yes

olympiads

3. It is known that for some positive coprime numbers $m$ and $n$, the numbers $m+1947 n$ and $n+1947 m$ have a common prime divisor $d>9$. Find the smallest possible value of the number $d$ under these conditions.

Answer: $d_{\min }=139$. For example, $$ \begin{aligned} & m=138, n=1 \rightarrow 1947 m+n=1947 \cdot 138+1=139 \cdot 1933 \\ & m+1947 n=138+1947=139 \cdot 15 \end{aligned} $$

139

Number Theory

math-word-problem

Yes

Yes

olympiads

Task 1. Answer: 6 hours.

Solution.  Using a bicycle reduces the operation time. For example, if Kolya starts by getting on the bicycle, he should ride it until passing it to Maksim at point $D$, which lies on segment AB. The position of point $D$ is determined by the condition: $$ \frac{f}{6}=\frac{48-f}{18} \rightarrow f=12 $$ The time to pass the bicycle: $$ t_{1}=\frac{48}{18+6}=2 . $$ During this time, Petya will walk 12 km towards city B and end up at point $F$. On segment $F D$, Petya and Maksim move towards each other, and to minimize the operation time, Maksim should pass the bicycle to Petya. This will happen at their meeting point $C$. The position of point $C$ on segment $F D$ is determined by the condition: $$ \left\{\begin{array}{l} \frac{d-12}{6}=\frac{e}{18} \rightarrow e=d=18 \\ e+d=36 \end{array}\right. $$ The time for Kolya to arrive in city B: $T_{1}=2+\frac{12}{6}=4 \text{ hours}$. The time for Petya to arrive in city B: $T_{2}=\frac{18}{6}+\frac{30}{18}=3+\frac{5}{3}=4 \text{ hours and } 40 \text{ minutes}$. The time for Maksim to arrive in city A: $T_{3}=2+1+3=6 \text{ hours}$. The minimum time for the operation to complete is 6 hours.

6

Other

math-word-problem

Incomplete

Yes

olympiads

Problem 6. Answer: $|L|_{\min }=\frac{a}{2} \sqrt{4 \lambda^{2}+6 \lambda+3}=7$.

Solution. $\lambda=\frac{1}{2}, a=2 \sqrt{7} \rightarrow|L|_{\min }=\left.\frac{a}{2} \sqrt{4 \lambda^{2}+6 \lambda+3}\right|_{\lambda=\frac{1}{2}, a=2 \sqrt{7}}=7$. ## Option 3

7

Algebra

math-word-problem

Incomplete

Yes

olympiads

1. The figure shows a cake in the form of a rectangle with sides $3 \times 3$. A straight line (cut) is also depicted,  intersecting the maximum number of squares, which is 5. The maximum number of cake pieces after the first cut is $2 \cdot 5 + 4 = 14$. Therefore, to cut all 9 squares, two straight lines are sufficient.

Answer: 14 pieces and 2 cuts.

14

Geometry

math-word-problem

Incomplete

Yes

olympiads

1. For Vasya's birthday, a cake with a square base of $4 \times 4$ dm was bought, divided into 16 equal pieces with square bases of $1 \times 1$ dm. Vasya decided to cut the cake with a knife along a straight line so that the maximum number of separate pieces, not necessarily equal, would be formed. What is the maximum number of pieces of cake that can be obtained with one straight cut? What is the minimum number of straight cuts needed to ensure that each of the 16 original pieces is cut?

Answer: 23 pieces and 3 cuts.

23

Geometry

math-word-problem

Yes

Incomplete

olympiads

1. For Kostya's birthday, a cake with a base in the shape of a $3 \times 5$ dm rectangle was bought, divided into 15 equal pieces with square bases of $1 \times 1$ dm. Kostya decided to cut the cake with a knife along a straight line to create the maximum number of separate pieces, not necessarily equal. What is the maximum number of pieces of cake that can be obtained with one straight cut? What is the minimum number of straight cuts needed to ensure that each of the 15 original pieces is cut?

Answer: 22 pieces and 3 cuts.

22

Geometry

math-word-problem

Yes

Incomplete

olympiads

1. For Masha's birthday, a cake with a base in the shape of a $2 \times 5$ dm rectangle was bought, divided into 10 equal pieces with square bases of $1 \times 1$ dm. Masha decided to cut the cake with a knife along a straight line to create the maximum number of separate pieces, not necessarily equal. What is the maximum number of pieces of cake that can be obtained with one straight cut? What is the minimum number of straight cuts needed to ensure that each of the 10 original pieces is cut?

Answer: 16 pieces and 2 cuts.

16

Geometry

math-word-problem

Yes

Incomplete

olympiads

1. Find the number of divisors of the number $a=2^{3} \cdot 3^{2} \cdot 5^{2}$, which are divisible by 3. Find the sum of such divisors.

1. Solution. Among the divisors of the number $a=2^{3} \cdot 3^{2} \cdot 5^{2}$, which are divisible by 3, the number 2 can be chosen with exponents $0,1,2,3$ (4 options), the number 3 - with exponents 1,2 (2 options), and the number 5 - with exponents $0,1,2$ (3 options). Therefore, the total number of divisors is $4 \cdot 2 \cdot 3=24$. The sum of the divisors of the number $b=2^{3} \cdot 5^{2}$ is $(1+2+4+8)(1+5+25)=465$. Then the sum of the divisors of the number $a$, which are divisible by 3, is $\left(3+3^{2}\right) \cdot 465=12 \cdot 465=5580$.

5580

Number Theory

math-word-problem

Yes

Yes

olympiads

2. How many integers $b$ exist such that the equation $x^{2}+b x-9600=0$ has an integer solution that is a multiple of both 10 and 12? Specify the largest possible $b$.

2. Solution. Since the desired integer solution $x$ is divisible by 10 and 12, it is divisible by 60, hence it can be written in the form $x=60 t, t \in Z$. Substitute $x=60 t$ into the original equation: $3600 t^{2}+60 b t-9600=0$. Express $b: b=\frac{160}{t}-60 t$. For $b$ to be an integer, $t$ must be a divisor of the number 160. $160=2^{5} \cdot 5$. The number $160=2^{5} \cdot 5$ has 12 positive divisors: $1,2,2^{2}, 2^{3}, 2^{4}, 2^{5}, 5,2 \cdot 5,2^{2} \cdot 5,2^{3} \cdot 5,2^{4} \cdot 5,2^{5} \cdot 5$. Taking the sign into account, we get 24 divisors. Each of them corresponds to a solution $x=60 t$ and an integer $b=\frac{160}{t}-60 t$. Therefore, the number of integers $b$ that satisfy the condition of the problem is 24. Since $b$ decreases as $t$ increases, the maximum $b$ corresponds to the smallest $t=-160$, so $b_{\max }=-1+60 \cdot 160=9599$.

9599

Algebra

math-word-problem

Yes

Yes

olympiads

3. How many three-digit positive numbers $x$ exist that are divisible by 3 and satisfy the equation $GCD(15, GCD(x, 20))=5$? Find the largest one.

3. Solution. Since 20 is not divisible by 3, $NOD(x, 20)$ is also not divisible by 3. Therefore, the equation $NOD(15, NOD(x, 20))=5$ is equivalent to the condition that $NOD(x, 20)$ is divisible by 5, which is possible if and only if $x$ is divisible by 5. Thus, the condition of the problem is equivalent to $x$ being divisible by 5 and by 3, that is, $x$ is divisible by 15. Therefore, $x$ can be written as $x=15m, m=1,2 \ldots$. The smallest three-digit $x=105$ is obtained when $m=7$, and the largest three-digit $x=990$ is obtained when $m=66$, making a total of 60 numbers.

60

Number Theory

math-word-problem

Yes

Yes

olympiads

4. The quadratic trinomial $p(x)=a x^{2}+b x+c, a>0$ when divided by ( $x-1$ ) gives a remainder of 4, and when divided by ( $x-2$ ) - a remainder of 15. Find the maximum possible value of the ordinate of the vertex of the parabola $y=p(x)$ under these conditions. For what value of $x$ is it achieved?

4. Solution. By the Remainder Theorem, the remainder of the division of a polynomial $p(x)$ by $x-a$ is $p(a)$. Therefore, the conditions of the problem are equivalent to the system: $\left\{\begin{array}{l}4 a+2 b+c=15 \\ a+b+c=4\end{array} \Rightarrow\left\{\begin{array}{l}b=11-3 a \\ c=2 a-7\end{array}\right.\right.$. Thus, $p(x)=a x^{2}+(11-3 a) x+2 a-7$. The minimum value of the quadratic trinomial $p(x)$ (the ordinate of the vertex of the parabola) is achieved at its vertex $x_{s}=\frac{3 a-11}{2 a}$. It is equal to $p_{\text {min }}(x)=p\left(x_{k}\right)=p\left(\frac{3 a-11}{2 a}\right)=-\frac{a^{2}-38 a+121}{4 a}=\frac{19}{2}-\frac{1}{4}\left(a+\frac{121}{a}\right)=4-\left(\sqrt{a}-\frac{11}{\sqrt{a}}\right)^{2}$. This value is maximal if and only if $\sqrt{a}-\frac{11}{\sqrt{a}}=0$, that is, $a=11$. When $a=11$, $x_{s}=1$, and $p\left(x_{s}\right)=4$.

4

Algebra

math-word-problem

Yes

Yes

olympiads

9. $k=9 t+8$, the number $5(9 t+8)(9 \cdot 25 t+222)$ is not divisible by 9; Problem 4 Answer: $R_{\text {min }}=10$, solutions $(-12 ; 3)$ and $(8 ; 3)$

Solution. \((x+8)(x-4)=4^{y} \rightarrow 1) x+8=2^{n}, x-4=2^{m}, m, n \in Z, m+n=2 y\) \(x>4 \rightarrow 2^{n}-8>4 \rightarrow n \geq 4, 2^{m}+4>4 \rightarrow m \geq 0\) \(2^{n}-2^{m}=12 \rightarrow 2^{m}(2^{n-m}-1)=2^{2} \cdot 3 \rightarrow m=2, n-m=2 \rightarrow n=4\) \(y_{1}=3, x_{1}=8\) - first solution. 2) \(x+8=-2^{n}, x-4=-2^{m}, m, n \in Z, m+n=2 y \rightarrow\) \(x<-8 \rightarrow -8-2^{n}<-8 \rightarrow n \geq 0, 4-2^{m}<-8 \rightarrow m \geq 4\) \(2^{m}-2^{n}=12 \rightarrow m=4, n=2 \rightarrow y_{2}=3, x_{2}=-12\) - second solution. \(R_{\min }=\frac{1}{2}\left|x_{1}-x_{2}\right|=10\) Problem 5 Answer: \(a=\frac{\pi}{2}+\pi k, k \in Z, k \geq 0\) Answer: \(a=\frac{\pi^{2}}{16}\) Solution  The figure shows the set of points on the plane corresponding to cases 1 and 2:  The following figure shows the set of points corresponding to the solutions of the second equation in the system  The overlap of parts of the figures containing an infinite number of points is possible when \(a=\frac{\pi}{2}+\pi k, k=0,1, \ldots\), Problem 6 Answer: \(2 \alpha=2 \operatorname{arctg} \frac{\sqrt{3}}{2} \approx 81.8^{\circ}\) ## Solution The angle between the heights of adjacent cones is equal to the angle of the axial section of the cone.  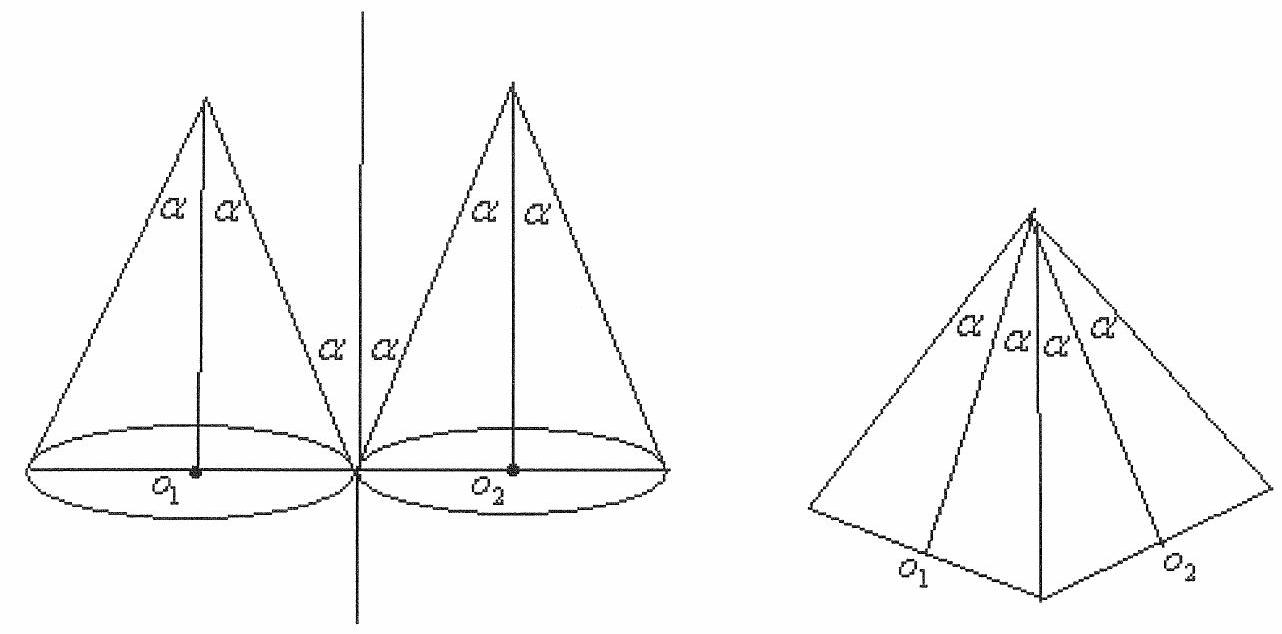The angle between the generators \(L_{1}\) and \(L_{2}\) of two adjacent cones, along which they touch the plane, is \(\frac{360^{\circ}}{n}\), where \(n\) is the number of cones.  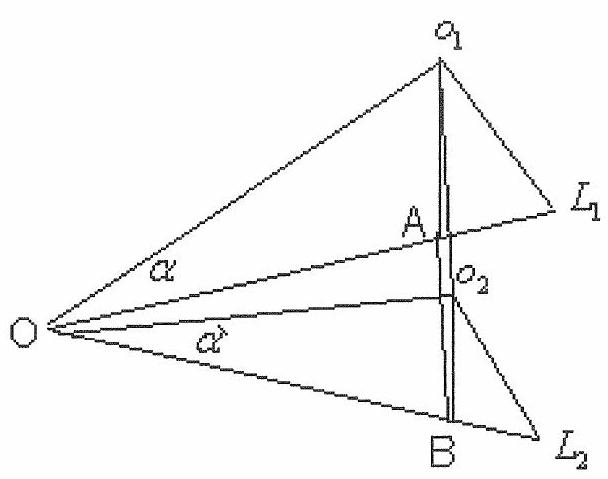\(\measuredangle o_{1} O o_{2}=2 \alpha, \measuredangle A O B=\frac{360^{\circ}}{n}, O o_{1}=O o_{2}=h, o_{1} o_{2}=2 h \sin \alpha\), \(A B=2 h \cos \alpha \sin \frac{180^{\circ}}{n} . \quad o_{1} O_{2}=A B \rightarrow \operatorname{tg} \alpha=\sin \frac{180^{\circ}}{n} \rightarrow 2 \alpha=2 \operatorname{arctg} \sin \frac{180^{\circ}}{n}\) In the case \(1 n=3\), therefore \(2 \alpha=2 \operatorname{arctg} \sin 60^{\circ}=2 \operatorname{arctg} \frac{\sqrt{3}}{2}\)

10

Number Theory

math-word-problem

More than one problem

Yes

olympiads

5. On the sides of triangle $A B C$ with side lengths 2, 3, and 4, external squares $A B B_{1} A_{1}, B C C_{2} B_{2}, C A A_{3} C_{3}$ are constructed. Find the sum of the squares of the side lengths of the hexagon $A_{1} B_{1} B_{2} C_{2} C_{3} A_{3}$. ## Answers and Solutions Problem 1 Answer: 165 m.

Solution $m$ - the number of steps Petya takes, $n$ - the number of steps Vova takes $0.75 m=0.55 n=L-$ path length $k$ - the step number of Petya leading to the coincidence of the footprint, $i$ - the step number of Vova leading to the coincidence of the footprint, $0.75 k=0.55 i \rightarrow 15 k=11 i \rightarrow\left\{\begin{array}{l}k=11 t \\ i=15 t\end{array}, t=0,1, \ldots T\right.$ Total number of footprints: $(m+1)+(n+1)-(T+1)=15 T+11 T-T+1=25 t+1=501 \rightarrow T=20$ $m=11 \cdot T=220 \rightarrow L=0.75 \cdot 220=165$ Problem 2 Answer: $x=6, y=55$ or $x=55, y=6$ Solution $y(x-5)=5(x+5) \rightarrow y=5+\frac{50}{x-5} \rightarrow x-5= \pm 1 ; \pm 2 ; \pm 5 ; \pm 10 ; \pm 25 ; \pm 50$ $y-5= \pm 50 ; \pm 25 ; \pm 10 ; \pm 5 ; \pm 2 ; \pm 1 \rightarrow x+y-10= \pm 51 ; \pm 27 ; \pm 15 ;$ The maximum value of $x+y$ is 61 and is achieved at $x=6, y=55$ or $x=55, y=6$ Problem 3 Answer: $a=-\frac{9}{8}, b=-6$ ## Solution When dividing the polynomial $P(x)=a x^{4}+3 x^{3}+b$ by $x-2$, we have the remainder $16 a+b+24=0$. Then $P(x)=(x-2)\left(a x^{3}+(2 a+3) x^{2}+(4 a+6) x+(8 a+12)\right)=(x-2) P_{1}(x)$ When dividing the polynomial $P_{1}(x)$ by $x-2$, we have the remainder $32 a+36=0 \rightarrow a=-\frac{9}{8} \rightarrow b=-6$. Problem 4 Answer: $a=2$ Solution Condition for the existence of roots: $\frac{D}{4}=16(a-1)^{2}+8(a-4) \geq 0 \rightarrow 2 a^{2}-3 a-2 \geq 0 \rightarrow a \in(-\infty ;-0.5] \cup[2 ;+\infty)$. $x_{1}^{2}+x_{2}^{2}=\left(x_{1}+x_{2}\right)^{2}-2 x_{1} x_{2}=(a-1)^{2}-\frac{4-a}{4}=a^{2}-\frac{7 a}{4}$ We need to find the minimum of this quadratic trinomial on the set $(-\infty ;-0.5] \cup[2 ;+\infty)$. The abscissa of its vertex $a=\frac{7}{8}$ is closer to 2 than to $-0.5$, since $2-\frac{7}{8}=\frac{9}{8}<\frac{7}{8}+\frac{1}{2}=\frac{11}{8}$. Therefore, the minimum possible value of the sum of the squares of the roots of the equation is achieved at $a=2$. Problem 5 Answer: 116 Solution  Additional construction: $B C=C K=a, M$ - midpoint of side $A B$. $\square A C K=\square C_{2} C B_{3}=\square K C B_{3}=180^{\circ}-\square B C A$ $\square A C K={ }_{B_{3} C C_{2} \rightarrow C_{2} B_{3}=A K=2 C M}$ $C M^{2}=\frac{2 a^{2}+2 b^{2}-c^{2}}{4} \rightarrow C_{2} B_{3}{ }^{2}=2 a^{2}+2 b^{2}-c^{2}$ Similarly, $$ B_{1} B_{2}{ }^{2}=2 a^{2}+2 b^{2}-c^{2}, \quad A_{1} A_{3}{ }^{2}=2 b^{2}+2 c^{2}-a^{2} $$ $A_{1} A_{2}{ }^{2}=c^{2}, B_{2} C_{2}{ }^{2}=a^{2}, A_{3} B_{3}{ }^{2}=b^{2}$ Combining, we arrive at the sum $\sigma^{2}$ of the squares of the sides of the hexagon being $4\left(a^{2}+b^{2}+c^{2}\right) \cdot$ In the conditions of the variant $1 a=2, b=3, c=4$, therefore $\sigma^{2}=4(4+9+16)=116$

116

Geometry

math-word-problem

Yes

Yes

olympiads

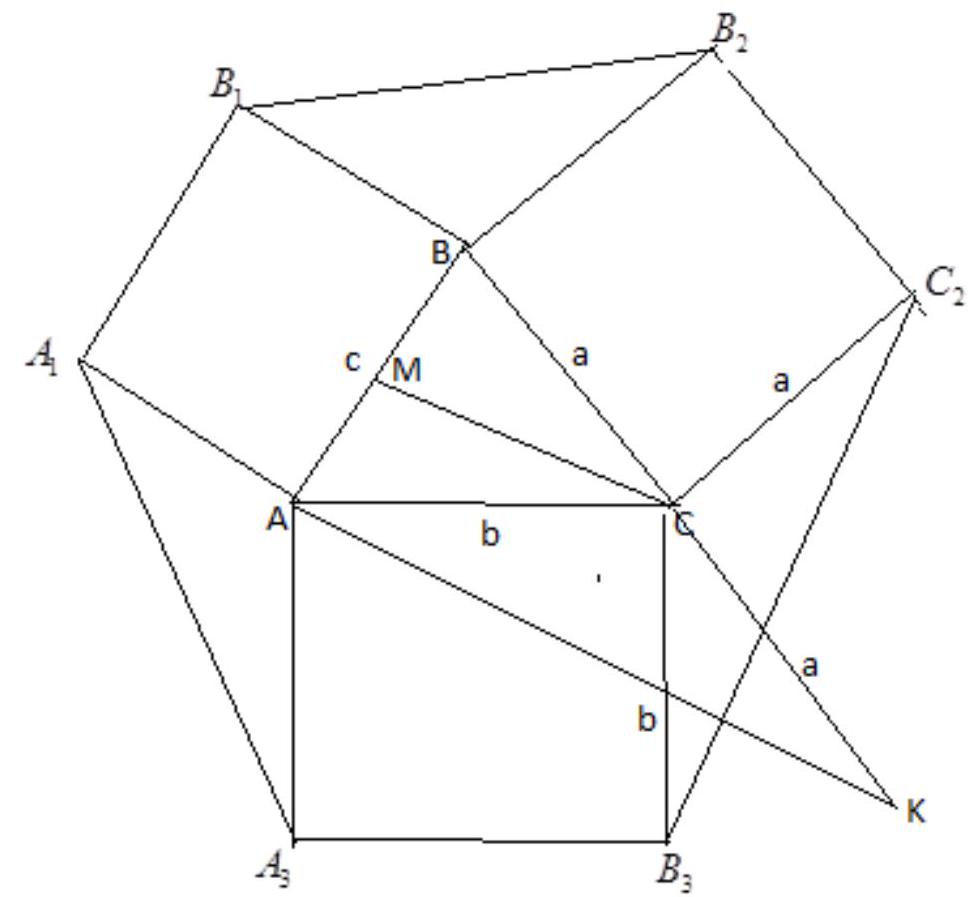
6. $x=p_{3}^{t}, y=p_{2}^{r} \cdot p_{1}^{q}, q=1,2, \ldots, k, r=1,2, \ldots, m, t=1,2, \ldots, n$. There are $k \cdot m \cdot n$ such pairs. Then the total number $N$ of different pairs of coprime divisors of the number $a$ is $N=(k+1)(m+1)(n+1)+k m+k n+m n+3 m n k=4 m n k+2(k m+k n+m n)+(m+n+k)+1$ In the variant $1 x=2 x_{1}, y=2 y_{1}$, where $x_{1}, y_{1}$ are coprime divisors of the number $540: 2=270=2 \cdot 3^{3} \cdot 5$. The number of different coprime pairs $\left(x_{1}, y_{1}\right)$ of divisors of the number $270=2 \cdot 3^{3} \cdot 5$ is obtained using the general formula $N$ for $k=1, m=3, n=1$ : $$ N=4 \cdot 3+2(3+1+3)+(1+3+1)+1=32 $$ Problem 4 Answer: $n_{\min }=5$

Solution. Let $a$ and $b$ (with $a > b$) be the lengths of the bases of the trapezoid (integers), and $p$ be a common divisor of $a$ and $b$. Then $a = p \cdot a_1$, $b = p \cdot b_1$. The trapezoid can be divided into equal triangles only as shown in the figure.  Extend the trapezoid to form triangle $AED$ by extending its lateral sides until they intersect at point $E$. Divide the base $AD$ of trapezoid $ABCD$ into $a_1$ segments of length $p$ and draw lines through their endpoints parallel to sides $AE$ and $DE$ respectively. Connect the points of intersection of these lines with sides $AE$ and $DE$ by lines parallel to base $AD$. Since $BC$ is parallel to $AD$, the constructed lines will divide $BC$ into $b_1$ segments of length $p$. The total number of equal triangles into which triangle $AED$ is divided is $a_1^2$, and among them, $b_1^2$ triangles belong to triangle $BEC$. Then the number $n$ of triangles into which trapezoid $ABCD$ will be divided is $n = a_1^2 - b_1^2 = \frac{a^2 - b^2}{p^2}$. The smallest value of $n$ corresponds to $p = \text{GCD}(a, b)$. In the case of $a = 108 = 2^2 \cdot 3^3$, $b = 72 = 2^3 \cdot 3^2$, $\text{GCD}(a, b) = 2^2 \cdot 3^2 = 36$. Then $n_{\text{min}} = \frac{108^2 - 72^2}{36^2} = \frac{36^2 \cdot 9 - 36^2 \cdot 4}{36^2} = 5$. Problem 5 Solution.  The construction uses standard problems: 1) constructing a line passing through a given point perpendicular to a given line; 2) constructing a line passing through a given point parallel to a given line; 3) constructing a triangle equal to a given one. Stages of construction:

5

Number Theory

math-word-problem

Incomplete

Yes

olympiads

4. Dima drew a parallelogram $A B C D$ and points $M$ and $N$ on sides $B C$ and $C D$ respectively such that $B M: M C=D N: N C=2: 3$. After that, he erased everything except points $A, M$ and $N$ using a cloth. Vova restored the drawing using a ruler and a compass. How did he do it?

4. Points $B$ and $D$ are the intersection points of lines $C M$ and $C N$ with the line passing through point $O$ and parallel to line $M N$. ## Problem 5 Numbers $A$, when divided by $n$, have a remainder of $r$, when divided by $n+1$ - a remainder of $r+1$, and when divided by $n+2$ - a remainder of $r+2$, have the form: $A=n(n+1)(n+2) t-n+r, A_{\min }$ corresponds to $t=1$ In the variant $1 n=11, r=5 \rightarrow A_{\min }=1710$

1710

Geometry

math-word-problem

Yes

Yes

olympiads

1. Pasha, Masha, Tolya, and Olya ate 88 candies, and each of them ate at least one candy. Masha and Tolya ate 57 candies, but Pasha ate the most candies. How many candies did Olya eat?

Solution. Either Masha or Tolya ate no less than 29 candies, then Pasha ate no less than 30 candies. Then the number of candies eaten by Pasha, Masha, and Tolya is no less than $57+30=87$. Since there are a total of 88 candies, and Olya did not refuse any candies, she gets one candy. Answer: 1 candy.

1

Logic and Puzzles

math-word-problem

Yes

Yes

olympiads

4. Pete is trying to lay out a square on a table using identical cardboard rectangles measuring $14 \times 10$. Will he be able to do this? Propose your version of constructing such a square. What is the minimum number of rectangles he will need?

Solution. Let $n$ be the number of rectangles that form the square. Then the area of the square is $S=14 \cdot 10 \cdot n$. If the side of the square is formed by $m$ sides of length 14 and $k$ sides of length 10, then the length of the side of the square is $14 m + 10 k$, and its area is $S=(14 m + 10 k)^{2}$. Equating the expressions for the areas, we get $$ 14 \cdot 10 \cdot n = (14 m + 10 k)^{2} \rightarrow 7 \cdot 5 \cdot n = (7 m + 5 k)^{2} $$ We can assume that the numbers $m$ and $k$ are coprime. Otherwise, the side of the square can be reduced by a factor of $p > 1$, where $p$ is a common divisor of $m$ and $k$. The left-hand side of the equation (*) is divisible by 7, so the number $7 m + 5 k$ is divisible by 7, and $(7 m + 5 k)^{2}$ is divisible by 49. Therefore, the left-hand side of (*) is divisible by 49, which is possible only if $n$ is divisible by 7. Similarly, it can be shown that $n$ is divisible by 5. Thus, $n = 35 \cdot s, s \in \mathbb{Z}$, and the smallest possible number of rectangles is $n = 35$. The figure below shows a square assembled from 35 rectangles.  Answer: 35 rectangles.

35

Geometry

math-word-problem

Yes

Yes

olympiads

5. In a rectangular table, the letters of the word "олимпиада" (olympiada) are arranged in a certain order. | $\mathrm{O}$ | Л | И | M | П | И | A | Д | A | | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | | Л | И | M | П | И | A | Д | A | O | | И | M | П | И | A | Д | A | O | Л | | M | П | И | A | Д | A | O | Л | И | You need to read the word "олимпиада" (olympiada), starting from the letter "O" located in the top-left corner of the table and ending with the letter "A". You are allowed to move from one letter to another if they are in adjacent cells of the table. Find the number of different ways to read the word "олимпиада" (olympiada) according to the given table.

Solution. In each cell of the table shown below | $\mathrm{O}$ | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | | | 1 | 3 | 6 | 10 | 15 | 21 | 28 | | | | 1 | 4 | 10 | 20 | 35 | 56 | | | | the number of different paths leading to the letter in that cell when reading the word "олимпиада" (Olympiada) is recorded. For example, in the cell in the third column and second row, i.e., to the letter $M$, there are three different ways to read "олим" (Olim): two paths from the cell in the second column and second row, and one path from the cell in the second column and first row. In general, to obtain the number in the cell at the intersection of row $i$ and column $j$, you need to add the number in the $(j-1)$-th cell of row $i$ and the number in the $j$-th cell of row $(i-1)$. In each of the shaded cells, where the last letter "A" of the word "олимпиада" (Olympiada) is located, the number of different ways to read this word, provided that the reading ends in this cell, is indicated. To get the answer, you need to add all the numbers in the highlighted cells: $n=56+28+8+1=93$. Answer: $n=93$. ## Answers for other variants. ## Variant 2

93

Combinatorics

math-word-problem

Yes

Yes

olympiads

4. Represent the number 43 as the sum of three prime numbers. In how many ways can this be done? Note that the number 1 is not considered a prime number.

Solution. $$ 43=a+b+c, a, b, c \text { - prime numbers. } $$ Prime numbers from 2 to 43 | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | 37 | 41 | 43 | | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | $a=2 \rightarrow 43-4=41 \rightarrow b=2 \rightarrow c=39-$ not a prime number. $a>2$ : list $a, 43-a$ and prime numbers $b, c$, for which $43-a=b+c$. | $a$ | 3 | 3 | 3 | 5 | 5 | 7 | 7 | 7 | 7 | 11 | 11 | 13 | 13 | 13 | | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | | $43-a$ | 40 | 40 | 40 | 38 | 38 | 36 | 36 | 36 | 36 | 32 | 32 | 30 | 30 | 30 | | $b$ | 3 | 11 | 17 | 7 | 19 | 5 | 7 | 13 | 17 | 3 | 13 | 7 | 11 | 17 | | $c$ | 37 | 29 | 23 | 31 | 19 | 31 | 29 | 23 | 19 | 29 | 19 | 23 | 19 | 13 | | $a$ | 17 | 17 | 17 | 19 | 19 | 19 | 23 | 23 | 29 | 29 | 31 | 37 | | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | | $43-a$ | 26 | 26 | 26 | 24 | 24 | 24 | 20 | 20 | 14 | 14 | 12 | 6 | | $b$ | 3 | 7 | 13 | 5 | 7 | 11 | 3 | 7 | 3 | 7 | 5 | 3 | | $c$ | 23 | 19 | 13 | 19 | 17 | 13 | 17 | 13 | 11 | 7 | 7 | 3 | Different triples of prime numbers, the sum of which is 43: $$ \begin{aligned} & 3+3+37,3+11+29,3+17+23,5+7+31,5+19+19,7+7+29, \\ & 7+13+23,7+17+19,11+13+19,13+17+13 \end{aligned} $$ Answer: ten ways.

10

Number Theory

math-word-problem

Yes

Yes

olympiads

5. The sum of the bases of the trapezoid is 4. Find the greatest possible length of the segment passing through the intersection of the diagonals of the trapezoid, parallel to its bases. 

Solution. Let $A D=a, B C=b, \frac{b}{a}=k$. $\square B O C \square A O D: \frac{O C}{A O}=\frac{O B}{D O}=\frac{b}{a}=k \rightarrow O C=k \cdot A O, A C=A O+O C=(1+k) A O$. $\square A O M \square A C B: \quad \frac{M O}{b}=\frac{A O}{A C}=\frac{1}{1+k} \rightarrow M O=\frac{b}{1+k}$. $\square O C N \square \triangle A C D: \quad \frac{O N}{a}=\frac{O C}{A C}=\frac{k}{1+k} \rightarrow O N=\frac{k a}{1+k}$. $M N=M O+O N=\frac{b}{1+k}+\frac{k a}{1+k}=\frac{b+k a}{1+k}=\frac{2 a b}{a+b}$. From $\sqrt{a b} \leq \frac{a+b}{2} \rightarrow M N \leq \frac{a+b}{2}$. Equality is achieved when $a=b$. Answer: $M N_{\max }=2$. ## Answers for other variants. ## 2nd variant

2

Geometry

math-word-problem

Incomplete

Yes

olympiads

Problem 3. Answer: $n=78$ #

# Solution: Given $a_{1}, a_{2} \neq 0$. The elements of the sequence are defined as long as $a_{n+1} \neq 0$. For other indices, the terms of the sequence are not defined. Let $a_{n+1} \neq 0, a_{n+2}=0$. Then for all $k \leq n \Rightarrow a_{k+2} a_{k+1}=a_{k+1} a_{k}-2$. The sequence $b_{k}=a_{k+1} a_{k}$ satisfies the relation $b_{k+1}=b_{k}-2$ and represents an arithmetic progression with a common difference $d=-2$ and the first term $b_{1}=a_{2} a_{1}=8 \cdot 19=152$. The general term of the sequence $b_{k}=b_{1}-2(k-1)$ equals zero if $2(k-1)=152 \Rightarrow k=77 \Rightarrow b_{77}=a_{77} \cdot a_{78}=0 \Rightarrow a_{78}=0$ Problem 4 Answer: $P(A)=\frac{1}{10} \cdot\left(\frac{2}{6^{2}}+\frac{27}{6^{3}}+\frac{104}{6^{4}}+\frac{205}{6^{5}}+\frac{252}{6^{6}}+\frac{210}{6^{7}}+\frac{120}{6^{8}}+\frac{45}{6^{9}}+\frac{10}{6^{10}}+\frac{1}{6^{11}}\right)=\frac{1}{10} \cdot\left(\frac{7^{10}}{6^{11}}-11 \frac{7^{3}}{6^{5}}\right)$ ## Solution If $n \geq 7$, then before the last roll that realizes event $A_{n}$, one of six mutually exclusive events $A_{n-1}, A_{n-2}, A_{n-3}, A_{n-4}, A_{n-5}, A_{n-6}$ must be realized. Then $$ A_{n}=B_{1} \cdot A_{n-1}+B_{2} \cdot A_{n-2}+B_{3} \cdot A_{n-3}+B_{4} \cdot A_{n-4}+B_{5} \cdot A_{n-5}+B_{6} \cdot A_{n-6}, $$ where $B_{1}, B_{2}, B_{3}, B_{4}, B_{5}, B_{6}$ are independent events of rolling $1,2,3,4,5,6$ on the last roll, $P\left(B_{k}\right)=p=\frac{1}{6}$ for all $k=1,2,3,4,5,6$. Considering the independence and mutual exclusivity of the events, from (3) follows the recursive formula for determining the probability $P\left(A_{n}\right):$ $$ P\left(A_{n}\right)=\frac{1}{6}\left(P\left(A_{n-1}\right)+P\left(A_{n-2}\right)+P\left(A_{n-3}\right)+P\left(A_{n-4}\right)+P\left(A_{n-5}\right)+P\left(A_{n-6}\right)\right) $$ The following table contains the probabilities of events consisting of rolling a total of $n$ points with $k$ rolls (for convenience, only the numerators of the fractions are written, the denominator in each row is $2^{-k}$, and the table is filled using relation (4), with the probability of an undefined or impossible event being zero) | $k \backslash n$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | | 2 | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 5 | 4 | 3 | 2 | | 3 | 0 | 0 | 0 | 1 | 3 | 6 | 10 | 15 | 21 | 25 | 27 | 27 | | 4 | 0 | 0 | 0 | 0 | 1 | 4 | 10 | 20 | 35 | 56 | 80 | 104 | | 5 | 0 | 0 | 0 | 0 | 0 | 1 | 5 | 15 | 35 | 70 | 126 | 205 | | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 6 | 21 | 56 | 126 | 252 | | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 7 | 28 | 84 | 210 | | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 8 | 36 | 120 | | 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 9 | 45 | | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 10 | | 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | It makes sense to roll the die from two to eleven times. Assuming that any number of rolls in this range is equally likely, the probability that a total of 11 points will be rolled from two to eleven times is $$ P(A)=\frac{1}{10} \cdot\left(\frac{2}{6^{2}}+\frac{27}{6^{3}}+\frac{104}{6^{4}}+\frac{205}{6^{5}}+\frac{252}{6^{6}}+\frac{210}{6^{7}}+\frac{120}{6^{8}}+\frac{45}{6^{9}}+\frac{10}{6^{10}}+\frac{1}{6^{11}}\right)=\frac{1}{10} \cdot\left(\frac{7^{10}}{6^{11}}-11 \frac{7^{3}}{6^{5}}\right) $$ Problem 5 Answer: $R \in\left(0 ; \frac{5-\sqrt{13}}{6} \pi\right)$ ## Solution: Transformation: $2 \sin \frac{2 x+3 y}{2} \cos \frac{2 x+3 y}{2}=2 \sin \frac{2 x+3 y}{2} \cos \frac{2 x-3 y}{2} \rightarrow$ $\rightarrow 2 \sin \frac{2 x+3 y}{2}\left(\cos \frac{2 x+3 y}{2}-\cos \frac{2 x-3 y}{2}\right)=-4 \sin \frac{2 x+3 y}{2} \sin \frac{3 y}{2} \sin x=0$ Case 1: $\sin \frac{2 x+3 y}{2}=0 \quad \rightarrow 2 x+3 y=2 \pi k, k \in Z$ The family of lines on the plane with equations (5) belongs to the set $M$. Case 2: $\sin \frac{3 y}{2}=0, x-$ any. $\sin \frac{3 y}{2}=0 \rightarrow y=\frac{2 \pi k}{3}, k \in Z$ The family of horizontal lines on the plane with equations (6) belongs to the set $M$. Case 3: $\sin x=0, y-$ any. $x

78

Number Theory

math-word-problem

Incomplete

Yes

olympiads

2. Find all numbers $C$ for which the inequality $|\alpha \sin x+\beta \cos 4 x| \leq C$ holds for all $x$ and any $(\alpha ; \beta)$ such that $|\alpha| \leq 1,|\beta| \leq 1$.

Answer: $\quad C \geq 2$

2

Inequalities

math-word-problem

Yes

Incomplete

olympiads

1. Customers of the online store "Ali-Express" live in five houses located at the vertices of a convex pentagon. One order was placed by residents of the first house, two orders by residents of the second house, and so on, with four orders from the residents of the fourth house. However, the residents of the last fifth house made 10 orders. The store manager is thinking about where to deliver all the orders so that the total distance traveled by all customers to pick up their items is minimized. Help him solve this problem and justify the result.

Answer: the goods should be delivered to the fifth house.

5

Geometry

math-word-problem

Yes

Problem not solved

olympiads

1. Customers of the online store "Ali-Express" live in four houses located at the vertices of a convex quadrilateral. One order was placed by residents of the first house, two orders by residents of the second house, three orders by residents of the third house, and six orders by residents of the last fourth house. The store manager is thinking about where to deliver all the orders so that the total distance traveled by all customers to pick up their items is minimized. Help him solve this problem and justify the result.

Answer: the goods should be delivered to the fourth house.

4

Geometry

math-word-problem

Yes

Problem not solved

olympiads

1. Petya considered moments of his life to be happy when his electronic watch showed the number of hours four times greater than the number of minutes or vice versa. Petya fell asleep and woke up at happy moments of his life, and he did not miss a single such moment. What is the maximum whole number of minutes Petya's sleep could have lasted?

Answer: 299 minutes or 241 minutes.

299

Number Theory

math-word-problem

Yes

Incomplete

olympiads

1. Petya considered moments of his life to be happy when his electronic watch showed the number of hours six times greater than the minutes or vice versa. Petya fell asleep and woke up at happy moments of his life, and he did not miss a single such moment. What is the maximum whole number of minutes Petya's sleep could have lasted?

Answer: 423 minutes or 361 minutes.

423

Number Theory

math-word-problem

Yes

Incomplete

olympiads

5. Let point $M$ divide edge $A B$ in the ratio $A M: M B=\lambda$, point $N$ divide edge $D C$ in the ratio $D N: N C=\mu$, and point $P$ divide edge $D B$ in the ratio $D P: P B=\theta$. We need to find the ratio $A Q: Q C$.  Let $T$ be the intersection point of line $P N$ with line $B C$, then point $Q$ is the intersection point of line $M T$ with line $A C$. Let $B M=a$, $C N=b$, and $B P=c$. Then $M A=\lambda a$, $N D=\mu b$, and $P D=\theta c$. Applying Menelaus' theorem to triangle $C B D$ and the transversal $P T$: $$ \frac{C T}{T B} \cdot \frac{B P}{P D} \cdot \frac{D N}{N C}=1 \quad \text{or} \quad \frac{C T}{T B} \cdot \frac{1}{\theta} \cdot \mu=1. $$ From this, we find $\frac{C T}{T B}=\frac{\theta}{\mu}$. Now, applying Menelaus' theorem to triangle $A C B$ and the transversal $M T$: $$ \frac{A Q}{Q C} \cdot \frac{C T}{T B} \cdot \frac{B M}{M A}=1 \quad \text{or} \quad \frac{A Q}{Q C} \cdot \frac{\theta}{\mu} \cdot \frac{1}{\lambda}=1. $$ From this, we get $$ \frac{A Q}{Q C}=\frac{\lambda \mu}{\theta} $$ According to the problem, $\lambda=2$, $\mu=3$, and $\theta=\frac{1}{2}$, then $\frac{A Q}{Q C}=12$.

Answer: $A Q: Q C=12$. #

12

Geometry

math-word-problem

Yes

Yes

olympiads

2. The number $a=2^{m} \cdot 3^{n}, m \geq 1, n \geq 1$ has a total of $(m+1)(n+1)$ divisors, and from the condition it follows that $m+1=2^{k_{1}} \cdot 3^{k_{2}}, n+1=2^{s_{1}} \cdot 3^{s_{2}}, k_{1}+s_{1} \leq m, k_{2}+s_{2} \leq n$. We have the following inequalities: $$ \begin{gathered} a \leq 1000 \rightarrow 2^{m} \cdot 3^{n} \leq 1000 \rightarrow 2^{m} \leq \frac{1000}{3} \rightarrow 2^{m} \leq 2^{8}=256 \rightarrow m+1 \leq 9 \\ 3^{n} \leq \frac{1000}{2} \rightarrow 3^{n} \leq 3^{5}=243 \rightarrow n+1 \leq 6 \end{gathered} $$ Considering that $m+1=2^{k_{1}} \cdot 3^{k_{2}}$, the possible values of $m+1$ are $m+1=2,3,4,6,8,9$. Similarly, $n+1=2^{s_{1}} \cdot 3^{s_{2}}$ can take the values $n+1=2,3,4,6$. The table contains all possible values of $a=2^{m} \cdot 3^{n}$ for such $m$ and $n$. For each pair of numbers $(m ; n)$ in the table (before calculating the corresponding number $a$), the numbers $k_{1}, k_{2}, s_{1}$, and $s_{2}$ are established, and the conditions $k_{1}+s_{1} \leq m, k_{2}+s_{2} \leq n$ are checked. The corresponding cell is then filled with the number $a=2^{m} \cdot 3^{n}$. Such cells (11 in total) are highlighted in the table, and the largest number $a \leq 1000$ recorded in them is 972.

Answer: 1) 11 numbers; 2) $a_{\max }=972$. | | | $n=1$ | $n=2$ | $n=3$ | $n=5$ | | :---: | :---: | :---: | :---: | :---: | :---: | | | $n+1$ | 2 | 3 | 4 | 6 | | $m=1$ | 2 | 6 | 18 | 54 | 486 | | $m=2$ | 3 | 12 | 36 | 108 | 972 | | $m=3$ | 4 | 24 | 72 | 216 | 1944 | | $m=5$ | 6 | 96 | 288 | 864 | 7776 | | $m=7$ | 8 | 384 | 1152 | 3456 | 31104 | | $m=8$ | 9 | 768 | 2304 | 6912 | 62208 |

972

Number Theory

math-word-problem

Incomplete

Yes

olympiads

5. In triangle $ABC$ with an area of 20, medians $AM, BN, CQ$ are drawn. On line $AC$, a point $P$ is taken such that $AP: PC = 2: 3$. Find the area of the quadrilateral with vertices at points $P, M, N, Q$.

Answer: $S_{1}=6, S_{2}=30$. #

6

Geometry

math-word-problem

Yes

Problem not solved

olympiads

5. In triangle $ABC$ with an area of 14, medians $AM, BN, CQ$ are drawn. On line $AC$, a point $P$ is taken such that $AP: PC = 4: 3$. Find the area of the quadrilateral with vertices at points $P, M, N, Q$.

Answer: $S_{1}=4, S_{2}=28$. Criteria for checking works, 11th grade Preliminary round of the sectoral physics and mathematics olympiad for schoolchildren "Rosatom", mathematics, field 2 #

4

Geometry

math-word-problem

Yes

Incomplete

olympiads

3. Represent the number 80 as the sum of two prime numbers. In how many ways can this be done? Let's remind you that one is not considered a prime number. Translate the above text into English, please keep the original text's line breaks and format, and output the translation result directly.

Solution. We organize the enumeration of all prime numbers from 2 to 73 in the form of a table. | 1 | 7 | 13 | 19 | 25 | 31 | 37 | 43 | 49 | 55 | 61 | 67 | 73 | | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | | 2 | 8 | 14 | 20 | 26 | 32 | 38 | 44 | 50 | 56 | 62 | 68 | 74 | | 3 | 9 | 15 | 21 | 27 | 33 | 39 | 45 | 51 | 57 | 63 | 69 | 75 | | 4 | 10 | 16 | 22 | 28 | 34 | 40 | 46 | 52 | 58 | 64 | 70 | 76 | | 5 | 11 | 17 | 23 | 29 | 35 | 41 | 47 | 53 | 59 | 65 | 71 | 77 | | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 78 | In the table, composite numbers from 4 to 78 are marked in dark color (1 is neither prime nor composite), and there are 21 prime numbers. In the following two tables, pairs of numbers $(a ; b)$ are listed for which $a+b=80$ and $a$ is a prime number. | a | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | | b | 78 | 77 | 75 | 73 | 69 | 67 | 63 | 61 | 57 | | a | 29 | 31 | 37 | 41 | 47 | 53 | 59 | 71 | | | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | | b | 51 | 49 | 43 | 39 | 33 | 27 | 21 | 9 | | In the second row of the table (b), composite numbers are marked in dark color. Thus, the number 80 can be represented as the sum of two prime numbers in four ways: $80=7+73, 80=13+67, 80=19+61, 80=37+43$. Answer: $80=7+73, 80=13+67, 80=19+61, 80=37+43$; four ways.

4

Combinatorics

MCQ

Yes

Yes

olympiads

4. On a sheet of paper, 12 consecutive integers are written. After one of them is crossed out, the sum of the remaining numbers equals 325. Which number was crossed out?

Solution. Let $n, n+1, \ldots, n+k-1, n+k, n+k+1, \ldots, n+11$ be 12 consecutive integers, and the number $n+k, k=0,1,2, \ldots, 11$ is crossed out. The sum of the numbers after crossing out is $$ \frac{2 n+11}{2} \cdot 12-(n+k)=325 \rightarrow 11 n+66-k=325 \rightarrow k=11 n-259 $$ Considering the condition $k \in[0 ; 11]$, we get $0 \leq 11 n-259 \leq 11 \rightarrow \frac{259}{11} \leq n \leq \frac{270}{11}$. In this interval, there is only one integer $n=24$ and $k=5$. Therefore, the crossed-out number is $n+k=29$. Answer: 29.

29

Number Theory

math-word-problem

Yes

Yes

olympiads

Task 1. Answer: 22 (23, if the start is considered) . #

# Solution. Case 1. The first and second cars are located on the same diameter. This happens at times $t_{1,2}^{k}$ (min), when the distance between the cars along the track is a multiple of half its length. $$ t_{1,2}^{k}=\frac{0.375}{3} \cdot 60 \cdot k=7.5 \cdot k, k=1,2, \ldots, 8 $$ Case 2. The first and third cars are located on the same diameter. This happens at times $t_{1,3}^{m}$ (min), when the distance between the cars along the track is a multiple of half its length. $$ t_{1,3}^{m}=\frac{0.375}{5} \cdot 60 \cdot m=4.5 \cdot m, m=1,2, \ldots, 13 $$ Case 3. The second and third cars are located on the same diameter. This happens at times $t_{2,3}^{n}$ (min), when the distance between the cars along the track is a multiple of half its length. $$ t_{2,3}^{n}=\frac{0.375}{2} \cdot 60 \cdot n=11.25 \cdot n, n=1,2, \ldots, 5 $$ Notation: $T_{1,2}=\left\{t_{1,2}^{k}\right\}, T_{1,3}=\left\{t_{1,3}^{m}\right\}, T_{2,3}=\left\{t_{2,3}^{n}\right\}$ - sets of time moments marked in cases $1-3$. We need to find the number $s(T)$ of elements of the set $T=T_{1,2} \cup T_{1,3} \cup T_{2,3}$. From the considered cases $1-3$ we have $s\left(T_{1,2}\right)=8, s\left(T_{1,3}\right)=13, s\left(T_{2,3}\right)=5$ The number of elements of pairwise intersections of sets: $$ \begin{aligned} & s\left(T_{1,2} \cap T_{1,3}\right)=2 \\ & 7.5 \cdot k=4.5 \cdot m \rightarrow 5 k=3 m \rightarrow\left\{\begin{array}{l} m=5 l \\ k=3 l \end{array}, l=1,2\right. \\ & s\left(T_{1,2} \cap T_{2,3}\right)=2 \\ & 7.5 \cdot k=11.25 \cdot n \rightarrow 2 k=3 n \rightarrow\left\{\begin{array}{l} n=2 l \\ k=3 l \end{array}, l=1,2\right. \\ & s\left(T_{1,3} \cap T_{2,3}\right)=2 \\ & 4.5 \cdot m=11.25 \cdot n \rightarrow 2 m=5 n \rightarrow\left\{\begin{array}{l} n=2 l \\ m=5 l \end{array}, l=1,2\right. \end{aligned} $$ Finally, the number of elements $s\left(T_{1,2} \cap T_{1,3} \cap T_{2,3}\right)$ is determined by the number of admissible triples $(k, m, n)$ for which $$ 7.5 k=4.5 m=11.25 n \rightarrow 5 k=3 m=7.5 n \rightarrow 10 k=6 m=15 n $$ Such triples have the form $n=2 l, m=5 l, k=3 l, l=1,2$ and there are two of them. By the general set formula $$ \begin{aligned} & s(T)=s\left(T_{1,2} \cup T_{1,3} \cup T_{2,3}\right)=s\left(T_{1,2}\right)+s\left(T_{1,3}\right)+s\left(T_{2,3}\right)-s\left(T_{1,2} \cap T_{1,3}\right)-s\left(T_{1,2} \cap T_{2,3}\right)- \\ & -s\left(T_{1,3} \cap T_{2,3}\right)+s\left(T_{1,2} \cap T_{1,3} \cap T_{2,3}\right)=8+13+5-2-2-2+2=22 \end{aligned} $$

22

Other

math-word-problem

Incomplete

Yes

olympiads

Task 2. Answer: 250. #

# Solution. $$ A=(5 n+1) 3^{n}-7=(5 n+1)(4-1)^{n}-7=4 B+(-1)^{n}(5 n+1)-7 $$ for some integer $B$. Then the divisibility of $A$ by 4 means the divisibility by 4 of the number $$ (-1)^{n}(5 n+1)-7 $$ Case $1 . n=2 k, k=1,2, \ldots 500$. $$ \begin{aligned} & (-1)^{n}(5 n+1)-7=10 k-6=4 m \rightarrow 5 k-2 m=3 \rightarrow\left[\begin{array}{l} k=1+2 s \\ m=1+5 s \end{array} \rightarrow n=4 s+2 \rightarrow\right. \\ & \rightarrow 1 \leq 4 s+2 \leq 1000 \rightarrow s=0,1, \ldots, 249 \end{aligned} $$ Case $2 . \quad n=2 k+1, k=0,1, \ldots 499$. $$ (-1)^{n}(5 n+1)-7=-(10 k+13)=4 m $$ The equation has no integer solutions.

250

Other

math-word-problem

Incomplete

Yes

olympiads

5. A football is sewn from 256 pieces of leather: white ones in the shape of hexagons and black ones in the shape of pentagons. Black pentagons only border white hexagons, and any white hexagon borders three black pentagons and three white hexagons. Find the number of white hexagons on the football.

Answer: 160. Criteria for checking works, 7th grade Preliminary round of the sectoral physics and mathematics olympiad for schoolchildren "Rosatom", mathematics #

160

Combinatorics

math-word-problem

Yes

Yes

olympiads

2. $n=2 k, k \in Z$ $m=\frac{1}{2}\left(4 k^{2}+8 a_{1} k-2 k+2-4 a_{1}\right)=2 k^{2}-k+1+2 a_{1}(k-1)$ will be an integer for any $k$, if $2 a_{1}-$ is an integer. Combining the two cases, we get $a_{1}=\frac{t}{2}, \quad t \in Z$. Let's find $t \in Z$, for which $m \geq n$ : $n^{2}+\left(4 a_{1}-1\right) n-4 a_{1}+2 \geq 2 n \rightarrow n^{2}+(2 t-3) n-2 t+2 \geq 0, \quad \forall n \geq 1$ $(n-1)(n+2 t-2) \geq 0$ For $n=1 \rightarrow m=1>0$. For $2-2 t \leq 2 \rightarrow t \geq 0$ the inequality $n \geq 2-2 t$ holds for all $n \geq 2$. For $t<0$ the inequality $m \geq n$ does not hold for $n=2,3, \ldots, 2 t-1$, so the condition of the problem is satisfied by $a_{1}=\frac{t}{2}, t \in Z, t \geq 0$. Problem 4

Solution We will use the property of GCD: $\forall a, b, c \in N \rightarrow \text{GCD}(a, b) = \text{GCD}(a, b + ac) \cdot$ Case 1. $x > y$. GCD $\left(x+y, x^{2}+2 y^{2}\right) = \text{GCD} \left(x+y, x^{2}+2 y^{2}+2(x+y)(x-y) = \text{GCD} \left(x+y, 3 x^{2}\right)\right)$ If $p \geq 4$ is a common divisor of the numbers $x+y$ and $3 x^{2}$, then $\text{GCD}(x, p) = p_{1} > 1$. Then $x$ is divisible by $p_{1}$, $x+y$ is divisible by $p_{1}$, and therefore $y$ is also divisible by $p_{1}$. Thus, $\text{GCD}(x, y) \geq p_{1} > 1$. The latter contradicts the mutual simplicity of $x$ and $y$. Case 2. $x < y$. GCD $\left(x+y, x^{2}+2 y^{2}\right) = \text{GCD} \left(x+y, x^{2}+2 y^{2}+(x+y)(y-x) = \text{GCD} \left(x+y, 3 y^{2}\right)\right)$. As in Case 1, the assumption of the existence of a common divisor $p \geq 4$ of the numbers $x+y$ and $y^{2}$ leads to a contradiction with the assumption of the mutual simplicity of $x$ and $y$. The inequality $\text{GCD} \left(x+y, x^{2}+2 y^{2}\right) \leq 2$ may not hold, for example, $x=7, y=5$, $\text{GCD} \left(x+y, x^{2}+2 y^{2}\right) = \text{GCD}(12,99)=3$. Problem 5 Answer: $a_{\text{min}} = 4$ Solution In the square $-9 \leq x \leq -4, 2 \leq y \leq 7$ there are exactly 36 integer pairs. All of them are solutions to the system if  $\left\{\begin{array}{c}-a-4 \leq -7 \\ \sqrt{a} \geq 2\end{array} \rightarrow a \geq 4\right.$. Thus, $a=4$ is the minimum number for which the system will have 36 integer solutions. Problem 6 Answer: $PQ = \frac{\sqrt{651}}{12} \approx 2.1$ Solution Case 1. The desired broken line exits the face $ASD$ through the edge $AS$ (or by symmetry through $SD$). Then the length of the segment $PQ$ on the net (see fig.) is the minimum length of the broken line. From $\square SPQ \quad PQ^{2} = PS^{2} + QS^{2} - 2 PS \cdot QS \cdot \cos 2\alpha$, where $\alpha$ is the angle at the vertex of the pyramid. $PS = \frac{n}{m+n} \cdot b, QS = \frac{q}{p+q} \cdot b, \cos 2\alpha = \frac{16 b^{4} - 24 a^{2} b^{2} + a^{4}}{16 b^{4} + 8 a^{2} b^{2} + a^{4}}$. In the variant $1, m=1, n=2, a=2, b=\sqrt{3}, p=1, q=3$. Then $PS = \frac{2 \sqrt{3}}{3}, QS = \frac{3 \sqrt{3}}{4}, \cos 2\alpha = -\frac{1}{2}$ and $PQ^{2} = \frac{217}{48} \rightarrow PQ = \frac{\sqrt{651}}{12} \approx 2.1$.  Case 2. The broken line exits through the edge $AD$. Then (see fig.) $PQ = \frac{p}{p+q} \cdot b + \frac{m}{m+n} \cdot b + a$. In the conditions of variant $1, PQ = 2 + \frac{7 \sqrt{3}}{12} \approx 3.0$

3

Algebra

math-word-problem

Incomplete

Yes

olympiads

4. For what least integer $n$ are all solutions of the equation $$ x^{3}-(5 n-9) x^{2}+\left(6 n^{2}-31 n-106\right) x-6(n-8)(n+2)=0 \text { greater than }-1 \text { ? } $$

Solution. Rewrite the equation as $$ x^{3}-(5 n-9) x^{2}+\left(6 n^{2}-31 n-106\right) x-6 n^{2}+36 n+96=0 . $$ Notice that $x_{1}=1>-1$ is a solution for all $n$ (the sum of the coefficients of the polynomial on the left side of the equation is zero for all $n$). Divide the equation by $x-1$: $$ x^{2}-5(n-2) x+6\left(n^{2}-6 n-16\right)=0 $$ The roots of this equation are: $x_{2}=3(n+2), x_{3}=2(n-8)$. We seek when these solutions are greater than -1: $$ \left\{\begin{array} { l } { 3 ( n + 2 ) > - 1 } \\ { 2 ( n - 8 ) > - 1 } \end{array} \rightarrow \left\{\begin{array}{l} n>-\frac{7}{3}, n \in Z \\ n>\frac{15}{2}, n \in Z \end{array} \rightarrow n \geq 8\right.\right. $$ Since $n$ is an integer, then $n \geq 8, n \in Z$. Answer: $n_{\min }=8$.

8

Algebra

math-word-problem

Yes

Yes

olympiads

5. The midline of a trapezoid is 4. A line parallel to the bases of the trapezoid and dividing its area in half intersects the lateral sides at points $M$ and $N$. Find the smallest possible length of the segment $M N$.

# Solution.  Notations: $A D=a, B C=b, C K=H, N E=h$ - heights of triangles $N C P$ and $D N Q$, $M N=x$ $$ S_{\text {AMND }}=S_{\text {MBCN }} \rightarrow \frac{x+b}{2} H=\frac{a+x}{2} h \rightarrow \frac{H}{h}=\frac{a+x}{x+b} $$ $\square N C P \quad \square D N Q \rightarrow \frac{H}{h}=\frac{x-b}{a-x} \rightarrow \frac{a+x}{x+b}=\frac{x-b}{a-x} \rightarrow a^{2}-x^{2}=x^{2}-b^{2} \rightarrow x=\sqrt{\frac{a^{2}+b^{2}}{2}}$. Since $a+b=8$, then $x=\sqrt{\frac{a^{2}+(8-a)^{2}}{2}}=\sqrt{a^{2}-16 a+32}=\sqrt{(a-4)^{2}+16}$. Answer: $M N_{\text {min }}=4$. ## Answers for other variants. ## Variant 2

4

Geometry

math-word-problem

Yes

Yes

olympiads

Task 1. Answer: $k=16$ collisions. A wire in the shape of a circle with radius $R$ has $m$ beads strung on it, equally spaced from each other. At a certain moment, $(m-1)$ beads are made to move with the same speed $v(1/$ sec) in the counterclockwise direction, while the remaining bead is made to move in the opposite direction at the same speed. It is assumed that after the collision of two beads, their speed remains unchanged, and the direction instantly reverses. How many collisions will occur between the beads in $T$ seconds.

16

Combinatorics

math-word-problem

Yes

Yes

olympiads

1. Find all $x$ that satisfy the inequality $n^{2} x^{2}-\left(2 n^{2}+n\right) x+n^{2}+n-6 \leq 0$ for any natural $n$.

Solution. The roots of the quadratic trinomial $n^{2} x^{2}-\left(2 n^{2}+n\right) x+n^{2}+n-6$ are $$ x_{1}=1-\frac{2}{n}, x_{2}=1+\frac{3}{n} $$ Factorize the left side of the inequality $$ n^{2}\left(x-\left(1-\frac{2}{n}\right)\right)\left(x-\left(1+\frac{3}{n}\right)\right) \leq 0 $$ Solving the inequality using the interval method, we get $x \in\left[1-\frac{2}{n} ; 1+\frac{3}{n}\right]$. Only $x=1$ belongs to this interval for any $n$. Answer: $x=1$

1

Inequalities

math-word-problem

Yes

Yes

olympiads

6. On the edges of a trihedral angle with vertex at point $S$, there are points $M, N$, and $K$ such that $S M^{2}+S N^{2}+S K^{2} \leq 12$. Find the area of triangle $S M N$, given that the angle $M S N$ is $30^{\circ}$, and the volume of the pyramid $S M N K$ is maximally possible.

Solution. Let's introduce the notations: $S M=m, S N=n, S K=k$.  The volume of the pyramid $S M N K$ is $$ V=\frac{1}{3} S_{S M N} \cdot h=\frac{1}{6} m n \sin \alpha \cdot h=\frac{1}{6} m n \sin \alpha \cdot k \sin \beta=\frac{\sin \alpha \sin \beta}{6} m n k . $$ The values of the angles $\alpha, \beta$ depend on the trihedral angle but not on the positions of the points $M, N, K$ on its edges. Therefore, the maximum volume of the pyramid $S M N K$ corresponds to the maximum value of the product $m \cdot n \cdot k$, given the condition $m^{2}+n^{2}+k^{2} \leq p$. From the inequality of the geometric mean and the arithmetic mean of three numbers, it follows that $\sqrt[3]{m^{2} n^{2} k^{2}} \leq \frac{m^{2}+n^{2}+k^{2}}{3} \leq \frac{p}{3}$ Equality is achieved when $m=n=k$. Then, when $m=n=k=\sqrt{\frac{p}{3}}$, the volume of the pyramid is maximized, and the area of the triangle $S M N$ takes the value $\frac{p \sin \alpha}{6}$. In our case, $p=12, \alpha=30^{\circ}$, so $S_{S M N}=1$. Answer: $S_{S M N}=1$. ## Answers for other variants. ## Variant 2

1

Geometry

math-word-problem

Yes

Yes

olympiads

5. Quadrilateral $ABCD$ is inscribed in a circle, and its diagonals intersect at point $P$. Points $K, L$, and $M$ are the midpoints of sides $AB, BC$, and $CD$ respectively. The radius of the circle circumscribed around triangle $KLP$ is 1. Find the radius of the circle circumscribed around triangle $LMP$. Problem 1 Answer: 18 passengers.

Solution. Let $y_{k}$ be the number of passengers in the car with number $k, k=1,2,3, \ldots, 10$. According to the problem, $\sum_{k=1}^{10} y_{k}=270$. Additionally, it is stated that $y_{2} \geq y_{1}+2, y_{3} \geq y_{1}+4, \ldots, y_{9} \geq y_{1}+16, \quad y_{10} \geq y_{1}+18$. Adding these inequalities, $$ y_{2}+y_{3}+\ldots+y_{9}+y_{10} \geq y_{1}+2+y_{1}+4+\ldots+y_{1}+16+y_{1}+18 $$ or $$ 270-y_{1} \geq 9 y_{1}+90 $$ From this, we get $y_{1} \leq 18$. From the conditions $y_{10} \geq y_{1}+18$ and $y_{10} \leq 2 y_{1}$, it follows that $2 y_{1} \geq y_{1}+18$ or $y_{1} \geq 18$. Comparing the obtained inequalities, we conclude that $y_{1}=18$. The set $y_{1}=18, y_{2}=20$, $\ldots, y_{10}=36$ satisfies the conditions of the problem. Problem 2 Answer: $x=\frac{8 \pi}{5}$. Solution. Introduce the notations: $u=\sin x, v=\sin 2 x, w=\sin 3 x$. Then the equation becomes $$ (u+v+w)^{3}=u^{3}+v^{3}+w^{3} $$ Rewrite the equation as $$ (u+v+w)^{3}-u^{3}-\left(v^{3}+w^{3}\right)=0 $$ Using the formulas for the difference and sum of cubes, as well as the difference of squares, factorize the left-hand side of the equation $$ \begin{aligned} & (u+v+w)^{3}-u^{3}-\left(v^{3}+w^{3}\right)=(v+w)\left((u+v+w)^{2}+u(u+v+w)+u^{2}\right)- \\ & -(v+w)\left(v^{2}-v w+w^{2}\right)=(v+w)\left[\left((u+v+w)^{2}-v^{2}\right)+\left(u^{2}-w^{2}\right)+u(u+w)+v(u+w)\right]= \\ & =(v+w)(u+w)(u+2 v+w+u-w+u+v))=3(v+w)(u+w)(u+v) \end{aligned} $$ As a result, the equation takes the form $$ 3(v+w)(u+w)(u+v)=0 $$ Returning to the original variables, we get the equation: Case $1 . \sin x+\sin 2 x=0$. $\left[\begin{array}{c}2 x=-x+2 \pi k \\ 2 x=\pi+x+2 \pi m\end{array} \rightarrow\left[\begin{array}{c}x=\frac{2 \pi k}{3}, \\ x=\pi+2 \pi m, m, k \in Z .\end{array}\right.\right.$ The largest solution on the interval $(0 ; 2 \pi)$ is $x=\frac{4 \pi}{3}$ Case $2 . \sin x+\sin 3 x=0$. $\left[\begin{array}{c}3 x=-x+2 \pi k \\ 3 x=\pi+x+2 \pi m\end{array} \rightarrow\left[\begin{array}{c}x=\frac{\pi k}{2}, \quad \text { The largest solution on the interval }(0 ; 2 \pi) \text { is } x=\frac{3 \pi}{2} \\ x=\frac{\pi}{2}+\pi m, m, k \in Z .\end{array} \quad\right.\right.$. Case $3 . \sin 3 x+\sin 2 x=0$. $\left[\begin{array}{c}3 x=-2 x+2 \pi k \\ 3 x=\pi+2 x+2 \pi m\end{array} \rightarrow\left[\begin{array}{c}x=\frac{2 \pi k}{5}, \quad \text { The largest solution on the interval }(0 ; 2 \pi) \text { is } x=\frac{8 \pi}{5} \\ x=\pi+2 \pi m, m, k \in Z .\end{array}\right.\right.$. The largest solution among $\frac{4 \pi}{3}, \frac{3 \pi}{2}, \frac{8 \pi}{5}$ is $x=\frac{8 \pi}{5}$. Problem 3 Answer: all 100 digits after the decimal point are nines. Solution. Consider $(7+4 \sqrt{3})^{2023}$. Use the binomial formula $$ (7+4 \sqrt{3})^{2023}=\sum_{k=0}^{2023} C_{2023}^{k} 7^{2023-k} \cdot(4 \sqrt{3})^{k}=a+b \sqrt{3} $$ where $a=\sum_{k=0}^{1011} C_{2023}^{2 k} 7^{2023-2 k} \cdot(4 \sqrt{3})^{2 k} \in N, b=\sum_{k=0}^{1011} C_{2023}^{2 k+1} 7^{2022-2 k} \cdot(4 \sqrt{3})^{2 k} \in N$. Now consider $(7-4 \sqrt{3})^{2023}:$ $$ (7-4 \sqrt{3})^{2023}=\sum_{k=0}^{2023} C_{2023}^{k} 7^{2023-k} \cdot(-4 \sqrt{3})^{k}=a-b \sqrt{3} $$ where $a=\sum_{k=0}^{1011} C_{2023}^{2 k} 7^{2023-2 k} \cdot(4 \sqrt{3})^{2 k} \in N, b=\sum_{k=0}^{1011} C_{2023}^{2 k+1} 7^{2022-2 k} \cdot(4 \sqrt{3})^{2 k} \in N$. Adding the obtained equalities, we get $$ (7+4 \sqrt{3})^{2023}+(7-4 \sqrt{3})^{2023}=a+b \sqrt{3}+a-b \sqrt{3}=2 a \in N $$ From this, we have $$ \begin{aligned} & (7+4 \sqrt{3})^{2023}=2 a-(7-4 \sqrt{3})^{2023}=2 a-\frac{(7-4 \sqrt{3})^{2023} \cdot(7+4 \sqrt{3})^{2023}}{(7+4 \sqrt{3})^{2023}}=2 a-\frac{1}{(7+4 \sqrt{3})^{2023}}= \\ & =2 a-1+1-\frac{1}{(7+4 \sqrt{3})^{2023}}, \quad 2 a-1 \in N . \end{aligned} $$ Notice that $\frac{1}{(7+4 \sqrt{3})^{2023}}0 $$ Then, considering the non-negativity of $x$, we find $x=\frac{\sqrt{2 \pm \sqrt{3}}}{4}$. It remains to check the condition $x \leq \frac{1}{2}$ : $$ \frac{\sqrt{2 \pm \sqrt{3}}}{4} \vee \frac{1}{2} \leftrightarrow \sqrt{2 \pm \sqrt{3}} \vee 2 \leftrightarrow 2 \pm \sqrt{3} \vee 4 \leftrightarrow \pm \sqrt{3} \vee 2 \rightarrow \pm \sqrt{3}<2 $$ Therefore, both roots $x=\frac{\sqrt{2+\sqrt{3}}}{2}$ and $x=\frac{\sqrt{2-\sqrt{3}}}{2}$ satisfy the condition $x \leq \frac{1}{2}$. Problem 5 Answer: $R=1$. Solution. Consider triangles $A B P$ and $D C P$. They are similar by two equal angles ( $\angle B A C=\angle B D C, . \angle A B D=\angle A D C$ as angles inscribed in a circle and subtending the same arc). Therefore, the sides of these triangles are proportional: $$ \frac{A B}{D C}=\frac{A P}{D P}=\frac{B P}{P C} $$ Now consider triangles $A K P$ and $D C P$. By the condition $A K=\frac{A B}{2}, D M=\frac{D C}{2}$, so $\frac{A K}{D M}=\frac{A B}{D C}$. As a result, we have $\frac{A K}{D M}=\frac{A P}{D B}$. Therefore, triangle $A P K$ is similar to triangle $D P M$ by an equal angle and proportional sides. Then the angle $A P K$ is equal to the angle $D P M$ as angles in similar triangles, lying opposite proportional sides. By the problem's condition, $K L$ and

1

Geometry

math-word-problem

Yes

Yes

olympiads

3. Find the first 1000 digits after the decimal point in the decimal representation of the number $(8+\sqrt{65})^{2022}$. Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.

Answer: all 1000 digits after the decimal point are zeros.

0

Number Theory

math-word-problem

Yes

Incomplete

olympiads

3. Find the first 200 digits after the decimal point in the decimal representation of the number $(7+5 \sqrt{2})^{2020}$. Translate the text above into English, please keep the original text's line breaks and format, and output the translation result directly.

Answer: all 200 digits after the decimal point are zeros.

0

Combinatorics

math-word-problem

Yes

Incomplete

olympiads

0.35 \cdot 160+0.1 x=0.2 \cdot 160+0.2 x, 0.15 \cdot 160=0.1 x, x=240 \text {. } $$ In total, it results in $160+240=400$ g of solution.

Answer: 400. ## Problem 9 Points $B_{1}$ and $C_{1}$ are the feet of the altitudes of triangle $ABC$, drawn from vertices $B$ and $C$ respectively. It is known that $AB=7, \quad AC=6, \sin \angle BAC=\frac{2 \sqrt{110}}{21}$. Find the length of the segment $B_{1}C_{1}$. ## Solution: Let the angle $\angle BAC$ be denoted by $\alpha$. There are two possible cases: 1) $00$. $$ \begin{aligned} & \frac{\left(x^{2}-4\right)(|2 x+2|+|x+4|)}{(2 x+2)^{2}-(x+4)^{2}}=a x^{2}, \\ & \frac{\left(x^{2}-4\right)(|2 x+2|+|x+4|)}{3\left(x^{2}-4\right)}=a x^{2}, \\ & |2 x+2|+|x+4|=3 a x^{2} . \end{aligned} $$ If $a \leq 0$, then the left side $>0$, and the right side $\leq 0$; equation ( ${ }^{*}$ ) has no solutions. If $a>0$, equation (*) has at least 2 solutions. The original equation can have fewer solutions only if at least one of the numbers $\pm 2$ is a solution ( ي $\left.^{2}\right)$. 2 is a solution of (*), if $12=12 a, a=1 ;(-2)$ is a solution of (*), if $4=12 a, a=1 / 3$. When $a=1$, equation (*) becomes $|2 x+2|+|x+4|=3 x^{2}$ and has roots $x_{1}=-1, x_{2}=2$. The original equation has a single root $x=-1$. When $a=1 / 3$, equation (*) becomes $|2 x+2|+|x+4|=x^{2}$ and has roots $x_{1}=-2, x_{2}=\frac{3+\sqrt{33}}{2}$. The original equation has a single root $x=\frac{3+\sqrt{33}}{2}$. Answer: the equation has no more than one root when $a \leq 0$, when $a=1 / 3$, and when $a=1$.

400

Algebra

math-word-problem

Yes

Yes

olympiads

0.6 \cdot 75+0.4 x=0.45 \cdot 75+0.45 x, 0.15 \cdot 75=0.05 x, x=225 \text {. } $$ In total, it results in $75+225=300$ g of solution.

Answer: 300. ## Problem 9 Points $B_{1}$ and $C_{1}$ are the feet of the altitudes of triangle $ABC$, drawn from vertices $B$ and $C$ respectively. It is known that $AB=8, \quad AC=7, \quad \sin \angle BAC=\frac{3 \sqrt{5}}{7}$. Find the length of the segment $B_{1} C_{1}$. ## Solution: Let the angle $\angle BAC$ be denoted by $\alpha$. There are two possible cases: 1) $00$. $$ \begin{gathered} \frac{\left(x^{2}-1\right)(|2 x+1|+|x+2|)}{(2 x+1)^{2}-(x+2)^{2}}=2 a x^{2} \\ \frac{\left(x^{2}-1\right)(|2 x+1|+|x+2|)}{3\left(x^{2}-1\right)}=2 a x^{2} \\ |2 x+1|+|x+2|=6 a x^{2} \end{gathered} $$ If $a \leq 0$, the left side $>0$, while the right side $\leq 0$; equation ( ${ }^{*}$ ) has no solutions. If $a>0$, equation ( ( $^{\prime}$ has at least 2 solutions. The original equation can have fewer solutions only if at least one of the numbers $\pm 1$ is a solution to $\left({ }^{2}\right)$. 1 is a solution to (*), if $6=6 a, a=1 ;(-1)$ is a solution to (*), if $2=6 a, a=1 / 3$. When $a=1$, equation (*) becomes $|2 x+1|+|x+2|=6 x^{2}$ and has roots $x_{1}=-1 / 2, x_{2}=1$. The original equation has a single root $x=-1 / 2$. When $a=1 / 3$, equation (*) becomes $|2 x+1|+|x+2|=2 x^{2}$ and has roots $x_{1}=-1, x_{2}=\frac{3+\sqrt{33}}{4}$. The original equation has a single root $x=\frac{3+\sqrt{33}}{4}$. Answer: the equation has one root when $a=1 / 3$ and when $a=1$.

300

Algebra

math-word-problem

Incomplete

Yes

olympiads