Datasets:

---

DenCT

/

leetcode-python-solutions-with-exaplanations

like 0

Simplest Greedy Python Solution | O(1) Space | O(n*k) Time

maximum-number-of-non-overlapping-palindrome-substrings

# Intuition\nIf there is a substring of size k + 2 which is a palindrome, then for sure there is a substring of size k which is a palindrome. Similarly, if there is a substring of size k + 3 which is a palindrome, then there is a substring of size k + 1 which is a palindrome.\n\n# Approach\nSo we can **greedily** start from 0th index and check for a substring of size k which is a palindrome, if not then size k + 1. *Then our new start index is either k or k + 1 based on which is a palindrome* and we can proceed similarly. *If both are not a palindrome then for sure we can\'t find any palindrome starting from that index*, so we move to next index.\n\n# Complexity\n- Time complexity:\n **O(nk)**\n O(n) for traversing the string and a factor of **"k" on each index** for checking whether s[i to i + k] its a palindrome or not by using the valid function.\n\n- Space complexity:\n **O(1)**\n\n# Code\n```\nclass Solution:\n \n def maxPalindromes(self, s: str, k: int) -> int:\n n = len(s)\n # function to check whether substring is a palindrome\n def valid(i, j):\n # if end index is greater then length of string\n if j > len(s):\n return False\n if s[i : j] == s[i : j][::-1]:\n return True\n return False\n maxSubstrings = 0\n start = 0\n while start < n:\n if valid(start, start + k):\n maxSubstrings += 1\n start += k\n elif valid(start, start + k + 1):\n maxSubstrings += 1\n start += k + 1\n else:\n # when there is no palindrome starting at that particular index \n start += 1\n return maxSubstrings\n```

You are given a string `s` and a **positive** integer `k`. Select a set of **non-overlapping** substrings from the string `s` that satisfy the following conditions: * The **length** of each substring is **at least** `k`. * Each substring is a **palindrome**. Return _the **maximum** number of substrings in an optimal selection_. A **substring** is a contiguous sequence of characters within a string. **Example 1:** **Input:** s = "abaccdbbd ", k = 3 **Output:** 2 **Explanation:** We can select the substrings underlined in s = "**aba**cc**dbbd** ". Both "aba " and "dbbd " are palindromes and have a length of at least k = 3. It can be shown that we cannot find a selection with more than two valid substrings. **Example 2:** **Input:** s = "adbcda ", k = 2 **Output:** 0 **Explanation:** There is no palindrome substring of length at least 2 in the string. **Constraints:** * `1 <= k <= s.length <= 2000` * `s` consists of lowercase English letters.

Easy Brute Force solution | Python | TC = O(n^3)

number-of-unequal-triplets-in-array

```\nclass Solution:\n def unequalTriplets(self, nums: List[int]) -> int:\n c = 0\n for i in range(len(nums)):\n for j in range(i+1, len(nums)):\n for k in range(j+1, len(nums)):\n if nums[i]!=nums[j] and nums[i]!=nums[k] and nums[j] != nums[k]:\n c+=1\n return c\n```

You are given a **0-indexed** array of positive integers `nums`. Find the number of triplets `(i, j, k)` that meet the following conditions: * `0 <= i < j < k < nums.length` * `nums[i]`, `nums[j]`, and `nums[k]` are **pairwise distinct**. * In other words, `nums[i] != nums[j]`, `nums[i] != nums[k]`, and `nums[j] != nums[k]`. Return _the number of triplets that meet the conditions._ **Example 1:** **Input:** nums = \[4,4,2,4,3\] **Output:** 3 **Explanation:** The following triplets meet the conditions: - (0, 2, 4) because 4 != 2 != 3 - (1, 2, 4) because 4 != 2 != 3 - (2, 3, 4) because 2 != 4 != 3 Since there are 3 triplets, we return 3. Note that (2, 0, 4) is not a valid triplet because 2 > 0. **Example 2:** **Input:** nums = \[1,1,1,1,1\] **Output:** 0 **Explanation:** No triplets meet the conditions so we return 0. **Constraints:** * `3 <= nums.length <= 100` * `1 <= nums[i] <= 1000`

Python Hashmap O(n) with diagrams

number-of-unequal-triplets-in-array

You can refer to this [video solution](https://youtu.be/d_CHEvI9gQU).\n\n\nLet\'s first try to understand the properties of the triplets.\n\n\n\n# Connected\n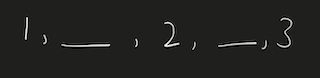\n\n\n\nIf we have these 3 numbers with multiple numbers between them, they will still be a triplet. \n\nSo, they don\'t have to be connected.\n\n\n# Ordering\n\n\n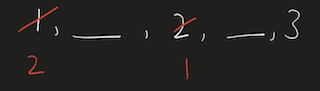\n\n\n\nIf we rearrange them, they will actually be the same triplet. \n\nSo, we can get a hint that ordering doesn\'t affect the number of triplets.\n\n\n\n\n# Repetition of Numbers\n\n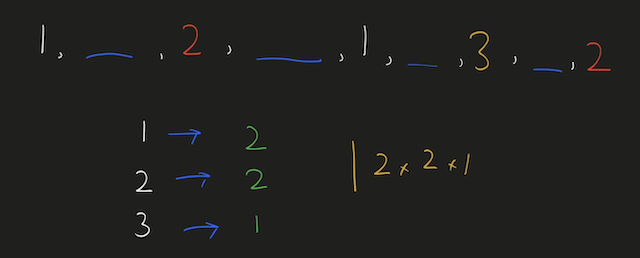\n\nLet\'s take the case where there is repetition of numbers.\n\nYou can again count that there are 4 valid triplets.\n\nThe ordering or the spacing/distance between the elements don\'t affect the answer.\n\nThe count of the triplets can also be calculated by multiplying the product of their frequencies `2*2*1`.\n\n# More than 4 distinct numbers\n\n\n\n\nLet\'s take a scenario where there are more than 3 distinct numbers to form triplets.\n\nHere, since we have to take 3 elements together, we can choose either of \n1. `1,2,3`\n2. `1,2,4`\n3. `2,3,4`\n\nThe count of these triplets would be the product of their individual frequencies.\n\nThe total count would be the addition of all these group.\n\n# Avoid Repetitive Counting \n\n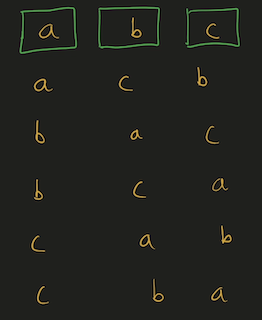\n\nThese are all the permutations for 3 elements.\n\nWe have to avoid counting repetitions of the same triplet.\n\n# Middle Element\n\n\n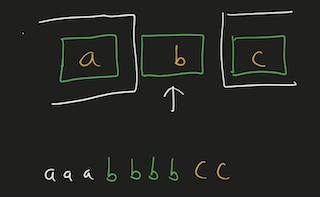\n\nThis can be avoided by fixing `b` as middle element and making sure that arrangement `c, a, b` never happens.\n\nIt can be a good idea to keep same elements contiguous. \nThis will make sure that we never consider palindromic triplets.\n\n# Left, Mid, Right\n\n\n\n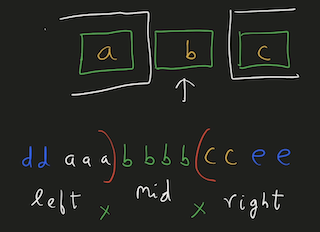\n\nThis will work even for more distinct elements on the left and right, as long as there are no same elements both on left & right.\n\nThis can\'t be the case since we already are keeping same elements together to avoid palindromic triplets.\n\nThe total number of triplets in this case, with the middle element `b` would be ```left * mid * right ```\nHere, \n1. `mid` would be the frequency of `b`\n2. `left` would be the number of elements on the left.\n3. `right` would be the number of elements on the right.\n\nWe can store the frequencies of elements in a HashMap.\n\n# Example\n\n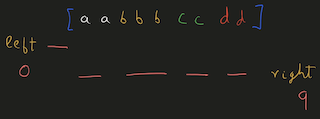\n\nWe can initialize `left=0, right=(no. of elements)` as shown in the diagram.\n\n# Iteration 1\n\n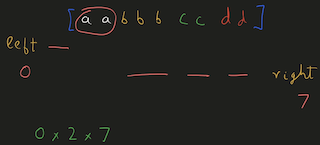\n\nEach time, we chose an element we decrement `right -= (frequency of element)`.\n\nAnd after we are done with that element, we will increment `left += (frequency of element)`.\n\nWe\'ll have to add the product of `left * freq * right` to result.\n\n# Iteration 2\n\n\n\n\nWhen we choose `b` to be the middle element, `left=2, right=4`.\n\n# Iteration 3\n\n\n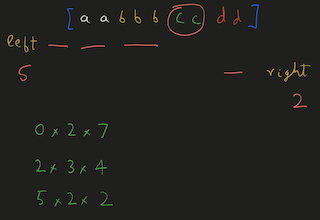\n\nWhen we choose `c` to be the middle element, `left=5, right=2`.\n\nAt the end, we will have to add all these products to our result.\n\n# Iteration 4\n\n\n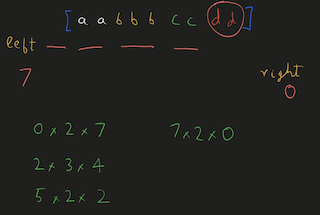\n\nWhen we choose `d` to be the middle element, `left=7, right=0`.\n\nNote: \n1. The first element will always have left-->0 \n2. The last element will have right-->0.\n\n# Time, Space Complexity\n\n`Time: O(n)` We are creating frequency map by iterating over the array.\n`Space: O(n)` We are using a HashMap to store the frequency of the elements.\n\nIf this was helpful, please leave a like, upvote, or even subscribe to the channel.\n\nCheers\n\n\n```\nclass Solution:\n def unequalTriplets(self, nums: List[int]) -> int:\n c = Counter(nums)\n res = 0\n \n left = 0\n right = len(nums)\n \n for _, freq in c.items():\n right -= freq\n res += left * freq * right\n left += freq\n \n return res\n

You are given a **0-indexed** array of positive integers `nums`. Find the number of triplets `(i, j, k)` that meet the following conditions: * `0 <= i < j < k < nums.length` * `nums[i]`, `nums[j]`, and `nums[k]` are **pairwise distinct**. * In other words, `nums[i] != nums[j]`, `nums[i] != nums[k]`, and `nums[j] != nums[k]`. Return _the number of triplets that meet the conditions._ **Example 1:** **Input:** nums = \[4,4,2,4,3\] **Output:** 3 **Explanation:** The following triplets meet the conditions: - (0, 2, 4) because 4 != 2 != 3 - (1, 2, 4) because 4 != 2 != 3 - (2, 3, 4) because 2 != 4 != 3 Since there are 3 triplets, we return 3. Note that (2, 0, 4) is not a valid triplet because 2 > 0. **Example 2:** **Input:** nums = \[1,1,1,1,1\] **Output:** 0 **Explanation:** No triplets meet the conditions so we return 0. **Constraints:** * `3 <= nums.length <= 100` * `1 <= nums[i] <= 1000`

✅ [Python/C++/JavaScript] O(n) beats 100%

number-of-unequal-triplets-in-array

# Intuition\nCalculate the `sum of prev freq & next freq and sum them`.\n\n# Approach\n1. Iterate over frequencies.\n2. Track the sum of previous frequencies.\n3. Track the sum of next frequences.\n4. Sum them all.\n#### Example\nLet `nums = [1, 3, 1, 2, 4]`\nFrequiencies: `1: 2, 3: 1, 2: 1, 4: 1`\n```\n prev frequency nxt count\n 0 2 5-2=3 0+(0*2*3)=0\n 2 1 3-1=2 0+(2*1*2)=4\n 3 1 2-1=1 4+(3*1*1)=7\n 4 1 1-1=0 4+(4*1*0)=7\nprev += freq nxt -= freq count += (prev * freq * nxt)\ncount = 7\n```\n\n\n# Code\n\n```python []\nclass Solution:\n def unequalTriplets(self, nums: List[int]) -> int:\n count = 0\n prev, nxt = 0, len(nums)\n for _, frequency in Counter(nums).items():\n nxt -= frequency\n count += prev * frequency * nxt\n prev += frequency\n return count\n```\n```C++ []\nclass Solution {\npublic:\n int unequalTriplets(vector<int>& nums) {\n int count = 0, prev = 0, nxt = nums.size();\n unordered_map<int, int> frequency;\n\n for (int n : nums) \n frequency[n]++;\n \n for (auto[n, freq] : frequency)\n {\n nxt -= freq;\n count += prev * freq * nxt;\n prev += freq;\n }\n return count;\n }\n};\n```\n```JavaScript []\nvar unequalTriplets = function(nums) {\n let count = 0,\n prev = 0,\n nxt = nums.length;\n let frequencies = nums.reduce((count, currentValue) => {\n return (count[currentValue] ? ++count[currentValue] : (count[currentValue] = 1), count);\n }, {});\n \n for (freq of Object.values(frequencies)) {\n nxt -= freq;\n count += (prev * freq * nxt);\n prev += freq\n }\n return count\n};\n```\n\n\n# Complexity\n- Time complexity: O(n)\n- Space complexity: O(n)

You are given a **0-indexed** array of positive integers `nums`. Find the number of triplets `(i, j, k)` that meet the following conditions: * `0 <= i < j < k < nums.length` * `nums[i]`, `nums[j]`, and `nums[k]` are **pairwise distinct**. * In other words, `nums[i] != nums[j]`, `nums[i] != nums[k]`, and `nums[j] != nums[k]`. Return _the number of triplets that meet the conditions._ **Example 1:** **Input:** nums = \[4,4,2,4,3\] **Output:** 3 **Explanation:** The following triplets meet the conditions: - (0, 2, 4) because 4 != 2 != 3 - (1, 2, 4) because 4 != 2 != 3 - (2, 3, 4) because 2 != 4 != 3 Since there are 3 triplets, we return 3. Note that (2, 0, 4) is not a valid triplet because 2 > 0. **Example 2:** **Input:** nums = \[1,1,1,1,1\] **Output:** 0 **Explanation:** No triplets meet the conditions so we return 0. **Constraints:** * `3 <= nums.length <= 100` * `1 <= nums[i] <= 1000`

[ Python ] ✅✅ Simple Python Solution Using Brute Force🥳✌👍

number-of-unequal-triplets-in-array

# If You like the Solution, Don\'t Forget To UpVote Me, Please UpVote! \uD83D\uDD3C\uD83D\uDE4F\n# Runtime: 1995 ms, faster than 33.33% of Python3 online submissions for Number of Unequal Triplets in Array.\n# Memory Usage: 14 MB, less than 33.33% of Python3 online submissions for Number of Unequal Triplets in Array.\n\n\tclass Solution:\n\t\tdef unequalTriplets(self, nums: List[int]) -> int:\n\n\t\t\tresult = 0\n\n\t\t\tfor i in range(len(nums)-2):\n\t\t\t\tfor j in range(i+1,len(nums)-1):\n\t\t\t\t\tfor k in range(j+1,len(nums)):\n\n\t\t\t\t\t\tif nums[i] != nums[j] and nums[j] != nums[k] and nums[i] != nums[k]:\n\t\t\t\t\t\t\tresult = result + 1\n\n\t\t\treturn result\n\n# Thank You \uD83E\uDD73\u270C\uD83D\uDC4D

You are given a **0-indexed** array of positive integers `nums`. Find the number of triplets `(i, j, k)` that meet the following conditions: * `0 <= i < j < k < nums.length` * `nums[i]`, `nums[j]`, and `nums[k]` are **pairwise distinct**. * In other words, `nums[i] != nums[j]`, `nums[i] != nums[k]`, and `nums[j] != nums[k]`. Return _the number of triplets that meet the conditions._ **Example 1:** **Input:** nums = \[4,4,2,4,3\] **Output:** 3 **Explanation:** The following triplets meet the conditions: - (0, 2, 4) because 4 != 2 != 3 - (1, 2, 4) because 4 != 2 != 3 - (2, 3, 4) because 2 != 4 != 3 Since there are 3 triplets, we return 3. Note that (2, 0, 4) is not a valid triplet because 2 > 0. **Example 2:** **Input:** nums = \[1,1,1,1,1\] **Output:** 0 **Explanation:** No triplets meet the conditions so we return 0. **Constraints:** * `3 <= nums.length <= 100` * `1 <= nums[i] <= 1000`

Python easy to read and well commented

number-of-unequal-triplets-in-array

# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def unequalTriplets(self, nums: List[int]) -> int:\n # iterate through nums 3 times, each time starting at previous iterator + 1\n # compare nums[i], [j], and [k]\n # if none of these are equal, increment a result\n\n result = 0\n\n for i in range(len(nums)):\n for j in range(i+1, len(nums)):\n for k in range(j+1, len(nums)):\n if nums[i] != nums[j] and nums[i] != nums[k] and nums[j] != nums[k]:\n result += 1\n\n return result\n```

You are given a **0-indexed** array of positive integers `nums`. Find the number of triplets `(i, j, k)` that meet the following conditions: * `0 <= i < j < k < nums.length` * `nums[i]`, `nums[j]`, and `nums[k]` are **pairwise distinct**. * In other words, `nums[i] != nums[j]`, `nums[i] != nums[k]`, and `nums[j] != nums[k]`. Return _the number of triplets that meet the conditions._ **Example 1:** **Input:** nums = \[4,4,2,4,3\] **Output:** 3 **Explanation:** The following triplets meet the conditions: - (0, 2, 4) because 4 != 2 != 3 - (1, 2, 4) because 4 != 2 != 3 - (2, 3, 4) because 2 != 4 != 3 Since there are 3 triplets, we return 3. Note that (2, 0, 4) is not a valid triplet because 2 > 0. **Example 2:** **Input:** nums = \[1,1,1,1,1\] **Output:** 0 **Explanation:** No triplets meet the conditions so we return 0. **Constraints:** * `3 <= nums.length <= 100` * `1 <= nums[i] <= 1000`

Python SortedList

closest-nodes-queries-in-a-binary-search-tree

# Intuition\nSadly, the tree is unbalanced. Can\'t do bineary search directly.\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nfrom sortedcontainers import SortedList\nclass Solution:\n def closestNodes(self, root: Optional[TreeNode], queries: List[int]) -> List[List[int]]:\n ans = []\n shortcut = SortedList()\n todo = []\n todo.append(root)\n while(todo):\n top = todo.pop()\n shortcut.add(top.val)\n if top.left:\n todo.append(top.left)\n if top.right:\n todo.append(top.right)\n for i in range(len(queries)):\n if queries[i] in shortcut:\n ans.append([queries[i], queries[i]])\n continue\n idx = shortcut.bisect_left(queries[i])\n if idx == 0:\n ans.append([-1, shortcut[0]])\n elif idx == len(shortcut):\n ans.append([shortcut[-1],-1])\n else:\n ans.append([shortcut[idx-1], shortcut[idx]])\n return ans\n\n \n```

You are given the `root` of a **binary search tree** and an array `queries` of size `n` consisting of positive integers. Find a **2D** array `answer` of size `n` where `answer[i] = [mini, maxi]`: * `mini` is the **largest** value in the tree that is smaller than or equal to `queries[i]`. If a such value does not exist, add `-1` instead. * `maxi` is the **smallest** value in the tree that is greater than or equal to `queries[i]`. If a such value does not exist, add `-1` instead. Return _the array_ `answer`. **Example 1:** **Input:** root = \[6,2,13,1,4,9,15,null,null,null,null,null,null,14\], queries = \[2,5,16\] **Output:** \[\[2,2\],\[4,6\],\[15,-1\]\] **Explanation:** We answer the queries in the following way: - The largest number that is smaller or equal than 2 in the tree is 2, and the smallest number that is greater or equal than 2 is still 2. So the answer for the first query is \[2,2\]. - The largest number that is smaller or equal than 5 in the tree is 4, and the smallest number that is greater or equal than 5 is 6. So the answer for the second query is \[4,6\]. - The largest number that is smaller or equal than 16 in the tree is 15, and the smallest number that is greater or equal than 16 does not exist. So the answer for the third query is \[15,-1\]. **Example 2:** **Input:** root = \[4,null,9\], queries = \[3\] **Output:** \[\[-1,4\]\] **Explanation:** The largest number that is smaller or equal to 3 in the tree does not exist, and the smallest number that is greater or equal to 3 is 4. So the answer for the query is \[-1,4\]. **Constraints:** * The number of nodes in the tree is in the range `[2, 105]`. * `1 <= Node.val <= 106` * `n == queries.length` * `1 <= n <= 105` * `1 <= queries[i] <= 106`

Easy Solution | Python Code

closest-nodes-queries-in-a-binary-search-tree

# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nGiven a BST.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Use Inorder traversal to get the node values as Sorted array.\n2. Create a set of the Array.\n3. Create ans array to store result of each query.\n4. Iterate through the queries array.\n5. For each element, check if it is in the set.\n6. If not in the set, use Binary search to get the (mini and maxi).\n7. I used bisect methods to find (mini and maxi).\n8. Return the 2-d ans array.\n\n\nHope it was clear. Thank you!\n\n# Complexity\n- Time complexity: O(n) + O(log n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def inorder(self, root):\n if root:\n self.inorder(root.left)\n self.A.append(root.val)\n self.inorder(root.right)\n \n \n def closestNodes(self, root: Optional[TreeNode], queries: List[int]) -> List[List[int]]:\n self.A = []\n\n self.inorder(root)\n \n net = set(self.A)\n \n # print(self.A)\n ans = []\n \n for q in queries:\n if q in net:\n k = [q, q]\n ans.append(k)\n else:\n i = bisect.bisect_right(self.A, q)\n maxi, mini = -1, -1\n if i < len(self.A):\n maxi = self.A[i]\n \n j = bisect.bisect_left(self.A, q)\n if j > 0:\n mini = self.A[j - 1]\n\n ans.append([mini, maxi])\n \n return ans\n \n```

You are given the `root` of a **binary search tree** and an array `queries` of size `n` consisting of positive integers. Find a **2D** array `answer` of size `n` where `answer[i] = [mini, maxi]`: * `mini` is the **largest** value in the tree that is smaller than or equal to `queries[i]`. If a such value does not exist, add `-1` instead. * `maxi` is the **smallest** value in the tree that is greater than or equal to `queries[i]`. If a such value does not exist, add `-1` instead. Return _the array_ `answer`. **Example 1:** **Input:** root = \[6,2,13,1,4,9,15,null,null,null,null,null,null,14\], queries = \[2,5,16\] **Output:** \[\[2,2\],\[4,6\],\[15,-1\]\] **Explanation:** We answer the queries in the following way: - The largest number that is smaller or equal than 2 in the tree is 2, and the smallest number that is greater or equal than 2 is still 2. So the answer for the first query is \[2,2\]. - The largest number that is smaller or equal than 5 in the tree is 4, and the smallest number that is greater or equal than 5 is 6. So the answer for the second query is \[4,6\]. - The largest number that is smaller or equal than 16 in the tree is 15, and the smallest number that is greater or equal than 16 does not exist. So the answer for the third query is \[15,-1\]. **Example 2:** **Input:** root = \[4,null,9\], queries = \[3\] **Output:** \[\[-1,4\]\] **Explanation:** The largest number that is smaller or equal to 3 in the tree does not exist, and the smallest number that is greater or equal to 3 is 4. So the answer for the query is \[-1,4\]. **Constraints:** * The number of nodes in the tree is in the range `[2, 105]`. * `1 <= Node.val <= 106` * `n == queries.length` * `1 <= n <= 105` * `1 <= queries[i] <= 106`

My weird binary search solution

closest-nodes-queries-in-a-binary-search-tree

# Overview\nappending an inorder traversal node values to an array from a BST tree will give you a sorted list in ascending order which you can use for a binary search.\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def closestNodes(self, root: Optional[TreeNode], queries: List[int]) -> List[List[int]]:\n output = []\n inorder = []\n \n def dfs(node):\n if not node:\n return\n \n dfs(node.left)\n inorder.append(node.val)\n dfs(node.right)\n \n dfs(root)\n for q in queries:\n smaller, greater = -1, -1\n l, r = 0, len(inorder)\n while l < r:\n m = l + (r - l) // 2\n if inorder[m] >= q:\n r = m\n else:\n l = m + 1\n \n greater = inorder[l] if l < len(inorder) else -1\n if l == len(inorder):\n smaller = inorder[-1]\n elif inorder[l] == q:\n smaller = q\n elif l - 1 >= 0 and inorder[l - 1] < q:\n smaller = inorder[l - 1]\n \n output.append([smaller, greater])\n \n \n return output\n \n \n \n \n```

You are given the `root` of a **binary search tree** and an array `queries` of size `n` consisting of positive integers. Find a **2D** array `answer` of size `n` where `answer[i] = [mini, maxi]`: * `mini` is the **largest** value in the tree that is smaller than or equal to `queries[i]`. If a such value does not exist, add `-1` instead. * `maxi` is the **smallest** value in the tree that is greater than or equal to `queries[i]`. If a such value does not exist, add `-1` instead. Return _the array_ `answer`. **Example 1:** **Input:** root = \[6,2,13,1,4,9,15,null,null,null,null,null,null,14\], queries = \[2,5,16\] **Output:** \[\[2,2\],\[4,6\],\[15,-1\]\] **Explanation:** We answer the queries in the following way: - The largest number that is smaller or equal than 2 in the tree is 2, and the smallest number that is greater or equal than 2 is still 2. So the answer for the first query is \[2,2\]. - The largest number that is smaller or equal than 5 in the tree is 4, and the smallest number that is greater or equal than 5 is 6. So the answer for the second query is \[4,6\]. - The largest number that is smaller or equal than 16 in the tree is 15, and the smallest number that is greater or equal than 16 does not exist. So the answer for the third query is \[15,-1\]. **Example 2:** **Input:** root = \[4,null,9\], queries = \[3\] **Output:** \[\[-1,4\]\] **Explanation:** The largest number that is smaller or equal to 3 in the tree does not exist, and the smallest number that is greater or equal to 3 is 4. So the answer for the query is \[-1,4\]. **Constraints:** * The number of nodes in the tree is in the range `[2, 105]`. * `1 <= Node.val <= 106` * `n == queries.length` * `1 <= n <= 105` * `1 <= queries[i] <= 106`

Python | runtime beats 100% python soln

closest-nodes-queries-in-a-binary-search-tree

# Approach\n- We can first store all the node values in an array to make searching part easy that will take O(n) time we can use inorder traversal so we don\'t have to sort the array.\n- Now for each query we can use binary search for closest smaller element and closest greater element that will take O(logn) time.\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def closestNodes(self, root: Optional[TreeNode], queries: List[int]) -> List[List[int]]:\n nums = []\n def inorder(root):\n if root:\n inorder(root.left)\n nums.append(root.val)\n inorder(root.right)\n inorder(root)\n ans = []\n l = len(nums)\n \n def binary_search(nums, x):\n left, right = 0, l-1\n a = -1\n b = -1\n \n while left <= right:\n mid = (left + right) // 2\n \n if x==nums[mid]:\n return [x, x]\n \n elif nums[mid]<x:\n a = nums[mid]\n left = mid+1\n \n else:\n right = mid-1\n \n \n left, right = 0, l-1\n b = -1\n \n while left <= right:\n mid = (left + right) // 2\n \n if nums[mid]>x:\n b = nums[mid]\n right = mid-1\n \n else:\n left = mid+1\n \n return [a, b]\n \n \n for target in queries:\n ans.append(binary_search(nums, target))\n \n return ans\n \n```\n**Upvote the post if you find it helpful.\nHappy coding.**

You are given the `root` of a **binary search tree** and an array `queries` of size `n` consisting of positive integers. Find a **2D** array `answer` of size `n` where `answer[i] = [mini, maxi]`: * `mini` is the **largest** value in the tree that is smaller than or equal to `queries[i]`. If a such value does not exist, add `-1` instead. * `maxi` is the **smallest** value in the tree that is greater than or equal to `queries[i]`. If a such value does not exist, add `-1` instead. Return _the array_ `answer`. **Example 1:** **Input:** root = \[6,2,13,1,4,9,15,null,null,null,null,null,null,14\], queries = \[2,5,16\] **Output:** \[\[2,2\],\[4,6\],\[15,-1\]\] **Explanation:** We answer the queries in the following way: - The largest number that is smaller or equal than 2 in the tree is 2, and the smallest number that is greater or equal than 2 is still 2. So the answer for the first query is \[2,2\]. - The largest number that is smaller or equal than 5 in the tree is 4, and the smallest number that is greater or equal than 5 is 6. So the answer for the second query is \[4,6\]. - The largest number that is smaller or equal than 16 in the tree is 15, and the smallest number that is greater or equal than 16 does not exist. So the answer for the third query is \[15,-1\]. **Example 2:** **Input:** root = \[4,null,9\], queries = \[3\] **Output:** \[\[-1,4\]\] **Explanation:** The largest number that is smaller or equal to 3 in the tree does not exist, and the smallest number that is greater or equal to 3 is 4. So the answer for the query is \[-1,4\]. **Constraints:** * The number of nodes in the tree is in the range `[2, 105]`. * `1 <= Node.val <= 106` * `n == queries.length` * `1 <= n <= 105` * `1 <= queries[i] <= 106`

Python3 | DFS + Binary Search Slow solution

closest-nodes-queries-in-a-binary-search-tree

# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity \n- Time complexity: O(n log n + q log n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def closestNodes(self, root: Optional[TreeNode], queries: List[int]) -> List[List[int]]:\n a, res, stack = [], [], [(root)]\n while stack:\n node = stack.pop()\n a.append(node.val)\n if node.left: stack.append(node.left)\n if node.right: stack.append(node.right)\n a.sort()\n for q in queries:\n mini, maxi, left, right = -1, -1, 0, len(a) - 1\n while left <= right:\n mid = (left + right) // 2\n if a[mid] <= q:\n mini = a[mid]\n left = mid + 1\n else: right = mid - 1\n left, right = 0, len(a) - 1\n while left <= right:\n mid = (left + right) // 2\n if a[mid] >= q:\n maxi = a[mid]\n right = mid - 1\n else: left = mid + 1\n res.append([mini, maxi])\n return res\n\n```

You are given the `root` of a **binary search tree** and an array `queries` of size `n` consisting of positive integers. Find a **2D** array `answer` of size `n` where `answer[i] = [mini, maxi]`: * `mini` is the **largest** value in the tree that is smaller than or equal to `queries[i]`. If a such value does not exist, add `-1` instead. * `maxi` is the **smallest** value in the tree that is greater than or equal to `queries[i]`. If a such value does not exist, add `-1` instead. Return _the array_ `answer`. **Example 1:** **Input:** root = \[6,2,13,1,4,9,15,null,null,null,null,null,null,14\], queries = \[2,5,16\] **Output:** \[\[2,2\],\[4,6\],\[15,-1\]\] **Explanation:** We answer the queries in the following way: - The largest number that is smaller or equal than 2 in the tree is 2, and the smallest number that is greater or equal than 2 is still 2. So the answer for the first query is \[2,2\]. - The largest number that is smaller or equal than 5 in the tree is 4, and the smallest number that is greater or equal than 5 is 6. So the answer for the second query is \[4,6\]. - The largest number that is smaller or equal than 16 in the tree is 15, and the smallest number that is greater or equal than 16 does not exist. So the answer for the third query is \[15,-1\]. **Example 2:** **Input:** root = \[4,null,9\], queries = \[3\] **Output:** \[\[-1,4\]\] **Explanation:** The largest number that is smaller or equal to 3 in the tree does not exist, and the smallest number that is greater or equal to 3 is 4. So the answer for the query is \[-1,4\]. **Constraints:** * The number of nodes in the tree is in the range `[2, 105]`. * `1 <= Node.val <= 106` * `n == queries.length` * `1 <= n <= 105` * `1 <= queries[i] <= 106`

Python Solution (beats-98%, iterative inorder, bisect)

closest-nodes-queries-in-a-binary-search-tree

# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe given tree is a BST so traversing it in inorder will give sorted list of node values. and then searching for result.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Traverse tree in inorder and store values in a List(iterative for space complexity optimisation)\n2. use bisect_left() function in bisect class to find the possible position of element in list.\n3. add conditionals as per question requirement (Look at the code)\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def closestNodes(self, root: Optional[TreeNode], queries: List[int]) -> List[List[int]]:\n stack, nodes = [], []\n def inorder(root):\n cur = root\n while cur or stack:\n while cur:\n stack.append(cur)\n cur = cur.left\n cur = stack.pop()\n nodes.append(cur.val)\n cur = cur.right\n inorder(root)\n\n res = []\n for q in queries:\n idx = bisect.bisect_left(nodes, q)\n if 0 <= idx < len(nodes) and nodes[idx] == q:\n res.append([q,q])\n else:\n if idx > 0 and idx < len(nodes):\n res.append([nodes[idx-1], nodes[idx]])\n elif idx <= 0:\n res.append([-1, nodes[idx]])\n elif idx >= len(nodes):\n res.append([nodes[idx-1], -1])\n return res \n \n```

You are given the `root` of a **binary search tree** and an array `queries` of size `n` consisting of positive integers. Find a **2D** array `answer` of size `n` where `answer[i] = [mini, maxi]`: * `mini` is the **largest** value in the tree that is smaller than or equal to `queries[i]`. If a such value does not exist, add `-1` instead. * `maxi` is the **smallest** value in the tree that is greater than or equal to `queries[i]`. If a such value does not exist, add `-1` instead. Return _the array_ `answer`. **Example 1:** **Input:** root = \[6,2,13,1,4,9,15,null,null,null,null,null,null,14\], queries = \[2,5,16\] **Output:** \[\[2,2\],\[4,6\],\[15,-1\]\] **Explanation:** We answer the queries in the following way: - The largest number that is smaller or equal than 2 in the tree is 2, and the smallest number that is greater or equal than 2 is still 2. So the answer for the first query is \[2,2\]. - The largest number that is smaller or equal than 5 in the tree is 4, and the smallest number that is greater or equal than 5 is 6. So the answer for the second query is \[4,6\]. - The largest number that is smaller or equal than 16 in the tree is 15, and the smallest number that is greater or equal than 16 does not exist. So the answer for the third query is \[15,-1\]. **Example 2:** **Input:** root = \[4,null,9\], queries = \[3\] **Output:** \[\[-1,4\]\] **Explanation:** The largest number that is smaller or equal to 3 in the tree does not exist, and the smallest number that is greater or equal to 3 is 4. So the answer for the query is \[-1,4\]. **Constraints:** * The number of nodes in the tree is in the range `[2, 105]`. * `1 <= Node.val <= 106` * `n == queries.length` * `1 <= n <= 105` * `1 <= queries[i] <= 106`

📌📌Python3 || ⚡1895 ms, faster than 94.70% of Python3

minimum-fuel-cost-to-report-to-the-capital

\n\n```\ndef minimumFuelCost(self, roads: List[List[int]], seats: int) -> int:\n adjacency_list = defaultdict(list)\n for a, b in roads:\n adjacency_list[a].append(b)\n adjacency_list[b].append(a) \n total_fuel_cost = [0] \n def dfs(node, parent):\n people = 1 \n for neighbor in adjacency_list[node]:\n if neighbor == parent:\n continue\n people += dfs(neighbor, node) \n if node != 0:\n total_fuel_cost[0] += math.ceil(people / seats) \n return people \n dfs(0, None)\n return total_fuel_cost[0]\n```\nThis code calculates the minimum fuel cost required to reach the capital city from all other cities. The code follows the following steps:\n1. Creation of adjacency list: The input roads list is converted into an adjacency list representation, where each city is a key and its corresponding neighbors are stored in a list. The dictionary adjacency_list is used for this purpose.\n1. Initializing the fuel cost: A list total_fuel_cost is created with a single element to store the minimum fuel cost, initialized to 0.\n1. Defining the DFS function: A recursive DFS function dfs is defined, which takes two arguments: the current node being processed and its parent node.\n1. Keeping track of the people: In each call of the DFS function, a variable people is used to keep track of the total number of people in the subtree rooted at the current node. Initially, the number of people is set to 1 to account for the person at the current node.\n1. Processing the neighbors: For each neighbor of the current node, the DFS function is called, and the number of people in the subtree rooted at the neighbor is added to the variable people. If the neighbor is the same as the parent, the loop continues to the next neighbor to avoid visiting the same node twice.\n1. Adding the fuel cost: If the current node is not the capital city (node 0), then the fuel cost to reach the capital city from this node is calculated. The formula used to calculate the fuel cost is math.ceil(people / seats). This cost is then added to the total fuel cost stored in total_fuel_cost[0].\n1. Returning the people: Finally, the function returns the number of people in the subtree rooted at the current node.\n1. Calling the DFS function: The DFS function is called with node 0 and None as the parent, which signifies that node 0 is the root of the tree and has no parent.\n1. Returning the result: The final result, which is the minimum fuel cost, is returned by the main function.

There is a tree (i.e., a connected, undirected graph with no cycles) structure country network consisting of `n` cities numbered from `0` to `n - 1` and exactly `n - 1` roads. The capital city is city `0`. You are given a 2D integer array `roads` where `roads[i] = [ai, bi]` denotes that there exists a **bidirectional road** connecting cities `ai` and `bi`. There is a meeting for the representatives of each city. The meeting is in the capital city. There is a car in each city. You are given an integer `seats` that indicates the number of seats in each car. A representative can use the car in their city to travel or change the car and ride with another representative. The cost of traveling between two cities is one liter of fuel. Return _the minimum number of liters of fuel to reach the capital city_. **Example 1:** **Input:** roads = \[\[0,1\],\[0,2\],\[0,3\]\], seats = 5 **Output:** 3 **Explanation:** - Representative1 goes directly to the capital with 1 liter of fuel. - Representative2 goes directly to the capital with 1 liter of fuel. - Representative3 goes directly to the capital with 1 liter of fuel. It costs 3 liters of fuel at minimum. It can be proven that 3 is the minimum number of liters of fuel needed. **Example 2:** **Input:** roads = \[\[3,1\],\[3,2\],\[1,0\],\[0,4\],\[0,5\],\[4,6\]\], seats = 2 **Output:** 7 **Explanation:** - Representative2 goes directly to city 3 with 1 liter of fuel. - Representative2 and representative3 go together to city 1 with 1 liter of fuel. - Representative2 and representative3 go together to the capital with 1 liter of fuel. - Representative1 goes directly to the capital with 1 liter of fuel. - Representative5 goes directly to the capital with 1 liter of fuel. - Representative6 goes directly to city 4 with 1 liter of fuel. - Representative4 and representative6 go together to the capital with 1 liter of fuel. It costs 7 liters of fuel at minimum. It can be proven that 7 is the minimum number of liters of fuel needed. **Example 3:** **Input:** roads = \[\], seats = 1 **Output:** 0 **Explanation:** No representatives need to travel to the capital city. **Constraints:** * `1 <= n <= 105` * `roads.length == n - 1` * `roads[i].length == 2` * `0 <= ai, bi < n` * `ai != bi` * `roads` represents a valid tree. * `1 <= seats <= 105`

✔️ Python Optimized Solution | Explained in Detail 🔥

minimum-fuel-cost-to-report-to-the-capital

**\uD83D\uDD3C IF YOU FIND THIS POST HELPFUL PLEASE UPVOTE \uD83D\uDC4D**\n\n**For Detailed Explaination Read this Blog:**\nhttps://www.python-techs.com/2023/02/minimum-fuel-cost-to-report-to-capital.html\n\n**Solution:**\n```\nfrom collections import defaultdict\n\nclass Solution:\n def minimumFuelCost(self, roads: List[List[int]], seats: int) -> int:\n # Create a dictionary to store the edges in the graph\n graph = defaultdict(list)\n for city_1, city_2 in roads:\n graph[city_1].append(city_2)\n graph[city_2].append(city_1)\n \n # Initialize the minimum fuel cost to 0\n minimum_fuel_cost = 0\n # Create a set to store the cities that have been visited\n visited_cities = set()\n \n # Define a helper function to traverse the graph\n def dfs(city):\n nonlocal minimum_fuel_cost\n # If the city has already been visited, return 0\n if city in visited_cities: return 0\n # Mark the city as visited\n visited_cities.add(city)\n # Initialize a variable to store the number of representatives in this city\n representatives = 0\n # Loop through the cities connected to this city\n for connected_city in graph[city]:\n # Recursively call the dfs function to count the number of representatives in the connected city\n connected_city_representatives = dfs(connected_city)\n # Calculate the number of cars needed to transport all the representatives in the connected city\n minimum_fuel_cost += (connected_city_representatives + seats - 1) // seats\n # Add the number of representatives in the connected city to the representatives variable\n representatives += connected_city_representatives\n # Return the number of representatives in this city, plus the representative from this city\n return representatives + 1\n \n # Call the dfs function starting from city 0 (the capital city)\n dfs(0)\n # Return the minimum fuel cost\n return minimum_fuel_cost\n```\n\n**Thank you for reading! \uD83D\uDE04 Comment if you have any questions or feedback.**

There is a tree (i.e., a connected, undirected graph with no cycles) structure country network consisting of `n` cities numbered from `0` to `n - 1` and exactly `n - 1` roads. The capital city is city `0`. You are given a 2D integer array `roads` where `roads[i] = [ai, bi]` denotes that there exists a **bidirectional road** connecting cities `ai` and `bi`. There is a meeting for the representatives of each city. The meeting is in the capital city. There is a car in each city. You are given an integer `seats` that indicates the number of seats in each car. A representative can use the car in their city to travel or change the car and ride with another representative. The cost of traveling between two cities is one liter of fuel. Return _the minimum number of liters of fuel to reach the capital city_. **Example 1:** **Input:** roads = \[\[0,1\],\[0,2\],\[0,3\]\], seats = 5 **Output:** 3 **Explanation:** - Representative1 goes directly to the capital with 1 liter of fuel. - Representative2 goes directly to the capital with 1 liter of fuel. - Representative3 goes directly to the capital with 1 liter of fuel. It costs 3 liters of fuel at minimum. It can be proven that 3 is the minimum number of liters of fuel needed. **Example 2:** **Input:** roads = \[\[3,1\],\[3,2\],\[1,0\],\[0,4\],\[0,5\],\[4,6\]\], seats = 2 **Output:** 7 **Explanation:** - Representative2 goes directly to city 3 with 1 liter of fuel. - Representative2 and representative3 go together to city 1 with 1 liter of fuel. - Representative2 and representative3 go together to the capital with 1 liter of fuel. - Representative1 goes directly to the capital with 1 liter of fuel. - Representative5 goes directly to the capital with 1 liter of fuel. - Representative6 goes directly to city 4 with 1 liter of fuel. - Representative4 and representative6 go together to the capital with 1 liter of fuel. It costs 7 liters of fuel at minimum. It can be proven that 7 is the minimum number of liters of fuel needed. **Example 3:** **Input:** roads = \[\], seats = 1 **Output:** 0 **Explanation:** No representatives need to travel to the capital city. **Constraints:** * `1 <= n <= 105` * `roads.length == n - 1` * `roads[i].length == 2` * `0 <= ai, bi < n` * `ai != bi` * `roads` represents a valid tree. * `1 <= seats <= 105`

[Python] Concise Solution || DFS

minimum-fuel-cost-to-report-to-the-capital

\n# Code\n```\nclass Solution:\n def minimumFuelCost(self, roads: List[List[int]], seats: int) -> int:\n def dfs(u):\n seen.add(u)\n nRep = 1 + sum(dfs(v) for v in tree[u] if v not in seen)\n ans[0] += ceil(nRep / seats) if u else 0\n return nRep\n tree, seen, ans = defaultdict(list), set(), [0]\n for u, v in roads: tree[u].append(v), tree[v].append(u)\n return not dfs(0) or ans[0]\n```

There is a tree (i.e., a connected, undirected graph with no cycles) structure country network consisting of `n` cities numbered from `0` to `n - 1` and exactly `n - 1` roads. The capital city is city `0`. You are given a 2D integer array `roads` where `roads[i] = [ai, bi]` denotes that there exists a **bidirectional road** connecting cities `ai` and `bi`. There is a meeting for the representatives of each city. The meeting is in the capital city. There is a car in each city. You are given an integer `seats` that indicates the number of seats in each car. A representative can use the car in their city to travel or change the car and ride with another representative. The cost of traveling between two cities is one liter of fuel. Return _the minimum number of liters of fuel to reach the capital city_. **Example 1:** **Input:** roads = \[\[0,1\],\[0,2\],\[0,3\]\], seats = 5 **Output:** 3 **Explanation:** - Representative1 goes directly to the capital with 1 liter of fuel. - Representative2 goes directly to the capital with 1 liter of fuel. - Representative3 goes directly to the capital with 1 liter of fuel. It costs 3 liters of fuel at minimum. It can be proven that 3 is the minimum number of liters of fuel needed. **Example 2:** **Input:** roads = \[\[3,1\],\[3,2\],\[1,0\],\[0,4\],\[0,5\],\[4,6\]\], seats = 2 **Output:** 7 **Explanation:** - Representative2 goes directly to city 3 with 1 liter of fuel. - Representative2 and representative3 go together to city 1 with 1 liter of fuel. - Representative2 and representative3 go together to the capital with 1 liter of fuel. - Representative1 goes directly to the capital with 1 liter of fuel. - Representative5 goes directly to the capital with 1 liter of fuel. - Representative6 goes directly to city 4 with 1 liter of fuel. - Representative4 and representative6 go together to the capital with 1 liter of fuel. It costs 7 liters of fuel at minimum. It can be proven that 7 is the minimum number of liters of fuel needed. **Example 3:** **Input:** roads = \[\], seats = 1 **Output:** 0 **Explanation:** No representatives need to travel to the capital city. **Constraints:** * `1 <= n <= 105` * `roads.length == n - 1` * `roads[i].length == 2` * `0 <= ai, bi < n` * `ai != bi` * `roads` represents a valid tree. * `1 <= seats <= 105`

Python optimal dfs solution

minimum-fuel-cost-to-report-to-the-capital

# Complexity\n- Time complexity of dfs:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n+e) => O(n+n-1) => O(n)\n\n- Space complexity of adjacency dictionary:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(e) => O(n-1) => O(n)\n\n# Code\n```\nclass Solution:\n def minimumFuelCost(self, roads: List[List[int]], seats: int) -> int:\n g=defaultdict(list)\n for i,j in roads:\n g[i].append(j)\n g[j].append(i)\n\n ans=0\n\n def dfs(i,par):\n nonlocal ans\n cost=1\n for ch in g[i]:\n if ch!=par:\n cost+=dfs(ch,i)\n\n if i!=0:\n ans+=ceil(cost/seats) \n return cost \n \n dfs(0,-1)\n return ans\n```

There is a tree (i.e., a connected, undirected graph with no cycles) structure country network consisting of `n` cities numbered from `0` to `n - 1` and exactly `n - 1` roads. The capital city is city `0`. You are given a 2D integer array `roads` where `roads[i] = [ai, bi]` denotes that there exists a **bidirectional road** connecting cities `ai` and `bi`. There is a meeting for the representatives of each city. The meeting is in the capital city. There is a car in each city. You are given an integer `seats` that indicates the number of seats in each car. A representative can use the car in their city to travel or change the car and ride with another representative. The cost of traveling between two cities is one liter of fuel. Return _the minimum number of liters of fuel to reach the capital city_. **Example 1:** **Input:** roads = \[\[0,1\],\[0,2\],\[0,3\]\], seats = 5 **Output:** 3 **Explanation:** - Representative1 goes directly to the capital with 1 liter of fuel. - Representative2 goes directly to the capital with 1 liter of fuel. - Representative3 goes directly to the capital with 1 liter of fuel. It costs 3 liters of fuel at minimum. It can be proven that 3 is the minimum number of liters of fuel needed. **Example 2:** **Input:** roads = \[\[3,1\],\[3,2\],\[1,0\],\[0,4\],\[0,5\],\[4,6\]\], seats = 2 **Output:** 7 **Explanation:** - Representative2 goes directly to city 3 with 1 liter of fuel. - Representative2 and representative3 go together to city 1 with 1 liter of fuel. - Representative2 and representative3 go together to the capital with 1 liter of fuel. - Representative1 goes directly to the capital with 1 liter of fuel. - Representative5 goes directly to the capital with 1 liter of fuel. - Representative6 goes directly to city 4 with 1 liter of fuel. - Representative4 and representative6 go together to the capital with 1 liter of fuel. It costs 7 liters of fuel at minimum. It can be proven that 7 is the minimum number of liters of fuel needed. **Example 3:** **Input:** roads = \[\], seats = 1 **Output:** 0 **Explanation:** No representatives need to travel to the capital city. **Constraints:** * `1 <= n <= 105` * `roads.length == n - 1` * `roads[i].length == 2` * `0 <= ai, bi < n` * `ai != bi` * `roads` represents a valid tree. * `1 <= seats <= 105`

[PYTHON] Simple Tree DFS O(N) solution

minimum-fuel-cost-to-report-to-the-capital

# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nFirst, Make tree.\nand calculate the number of representatives (In fact, this is the number of nodes)\nThe minimum number of liters of fuel for Node $n$ ($F_n$) can be calculate as follows:\n - $R_n =$ Number of representatives that must pass through the n node\n - $C_n =$ The children for node $n$.\n - $R_n = Sum_{c \\in C_n}(R_c)$\n - $F_n = ceil(R_n/seats)$\n\n# Complexity\n- Time complexity: $O(N)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(N)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python\nclass Solution:\n def minimumFuelCost(self, roads: List[List[int]], seats: int) -> int:\n G = defaultdict(list)\n for s, e in roads:\n G[s].append(e)\n G[e].append(s)\n total = 0\n def go(node, parent):\n nonlocal total\n accum = 1\n for n in G[node]:\n if n == parent:\n continue\n rep = go(n, node)\n total += (rep + seats - 1) // seats\n accum += rep\n return accum\n go(0, -1)\n return total\n```

There is a tree (i.e., a connected, undirected graph with no cycles) structure country network consisting of `n` cities numbered from `0` to `n - 1` and exactly `n - 1` roads. The capital city is city `0`. You are given a 2D integer array `roads` where `roads[i] = [ai, bi]` denotes that there exists a **bidirectional road** connecting cities `ai` and `bi`. There is a meeting for the representatives of each city. The meeting is in the capital city. There is a car in each city. You are given an integer `seats` that indicates the number of seats in each car. A representative can use the car in their city to travel or change the car and ride with another representative. The cost of traveling between two cities is one liter of fuel. Return _the minimum number of liters of fuel to reach the capital city_. **Example 1:** **Input:** roads = \[\[0,1\],\[0,2\],\[0,3\]\], seats = 5 **Output:** 3 **Explanation:** - Representative1 goes directly to the capital with 1 liter of fuel. - Representative2 goes directly to the capital with 1 liter of fuel. - Representative3 goes directly to the capital with 1 liter of fuel. It costs 3 liters of fuel at minimum. It can be proven that 3 is the minimum number of liters of fuel needed. **Example 2:** **Input:** roads = \[\[3,1\],\[3,2\],\[1,0\],\[0,4\],\[0,5\],\[4,6\]\], seats = 2 **Output:** 7 **Explanation:** - Representative2 goes directly to city 3 with 1 liter of fuel. - Representative2 and representative3 go together to city 1 with 1 liter of fuel. - Representative2 and representative3 go together to the capital with 1 liter of fuel. - Representative1 goes directly to the capital with 1 liter of fuel. - Representative5 goes directly to the capital with 1 liter of fuel. - Representative6 goes directly to city 4 with 1 liter of fuel. - Representative4 and representative6 go together to the capital with 1 liter of fuel. It costs 7 liters of fuel at minimum. It can be proven that 7 is the minimum number of liters of fuel needed. **Example 3:** **Input:** roads = \[\], seats = 1 **Output:** 0 **Explanation:** No representatives need to travel to the capital city. **Constraints:** * `1 <= n <= 105` * `roads.length == n - 1` * `roads[i].length == 2` * `0 <= ai, bi < n` * `ai != bi` * `roads` represents a valid tree. * `1 <= seats <= 105`

Python, DFS

minimum-fuel-cost-to-report-to-the-capital

```\nclass Solution:\n def minimumFuelCost(self, roads: List[List[int]], seats: int) -> int:\n def dfs(node, parent): \n people = 1\n for child in adj[node]:\n if child != parent:\n people += dfs(child, node)\n \n if node:\n self.result += (people - 1) // seats + 1\n \n return people\n \n adj = defaultdict(list)\n for a, b in roads:\n adj[a].append(b)\n adj[b].append(a)\n \n self.result = 0\n dfs(0, None)\n \n return self.result\n```

There is a tree (i.e., a connected, undirected graph with no cycles) structure country network consisting of `n` cities numbered from `0` to `n - 1` and exactly `n - 1` roads. The capital city is city `0`. You are given a 2D integer array `roads` where `roads[i] = [ai, bi]` denotes that there exists a **bidirectional road** connecting cities `ai` and `bi`. There is a meeting for the representatives of each city. The meeting is in the capital city. There is a car in each city. You are given an integer `seats` that indicates the number of seats in each car. A representative can use the car in their city to travel or change the car and ride with another representative. The cost of traveling between two cities is one liter of fuel. Return _the minimum number of liters of fuel to reach the capital city_. **Example 1:** **Input:** roads = \[\[0,1\],\[0,2\],\[0,3\]\], seats = 5 **Output:** 3 **Explanation:** - Representative1 goes directly to the capital with 1 liter of fuel. - Representative2 goes directly to the capital with 1 liter of fuel. - Representative3 goes directly to the capital with 1 liter of fuel. It costs 3 liters of fuel at minimum. It can be proven that 3 is the minimum number of liters of fuel needed. **Example 2:** **Input:** roads = \[\[3,1\],\[3,2\],\[1,0\],\[0,4\],\[0,5\],\[4,6\]\], seats = 2 **Output:** 7 **Explanation:** - Representative2 goes directly to city 3 with 1 liter of fuel. - Representative2 and representative3 go together to city 1 with 1 liter of fuel. - Representative2 and representative3 go together to the capital with 1 liter of fuel. - Representative1 goes directly to the capital with 1 liter of fuel. - Representative5 goes directly to the capital with 1 liter of fuel. - Representative6 goes directly to city 4 with 1 liter of fuel. - Representative4 and representative6 go together to the capital with 1 liter of fuel. It costs 7 liters of fuel at minimum. It can be proven that 7 is the minimum number of liters of fuel needed. **Example 3:** **Input:** roads = \[\], seats = 1 **Output:** 0 **Explanation:** No representatives need to travel to the capital city. **Constraints:** * `1 <= n <= 105` * `roads.length == n - 1` * `roads[i].length == 2` * `0 <= ai, bi < n` * `ai != bi` * `roads` represents a valid tree. * `1 <= seats <= 105`

Python | Clean DFS

minimum-fuel-cost-to-report-to-the-capital

# Code\n```\nfrom collections import defaultdict\n\nclass Solution:\n def minimumFuelCost(self, roads: List[List[int]], seats: int) -> int:\n G = defaultdict(list)\n for v, w in roads:\n G[v].append(w)\n G[w].append(v)\n ans = 0\n visited = set()\n def dfs(v):\n nonlocal ans\n if v in visited: return 0\n visited.add(v)\n res = 0\n for w in G[v]:\n cur = dfs(w)\n ans += (cur + seats - 1) // seats\n res += cur\n return res + 1\n dfs(0)\n return ans\n```

There is a tree (i.e., a connected, undirected graph with no cycles) structure country network consisting of `n` cities numbered from `0` to `n - 1` and exactly `n - 1` roads. The capital city is city `0`. You are given a 2D integer array `roads` where `roads[i] = [ai, bi]` denotes that there exists a **bidirectional road** connecting cities `ai` and `bi`. There is a meeting for the representatives of each city. The meeting is in the capital city. There is a car in each city. You are given an integer `seats` that indicates the number of seats in each car. A representative can use the car in their city to travel or change the car and ride with another representative. The cost of traveling between two cities is one liter of fuel. Return _the minimum number of liters of fuel to reach the capital city_. **Example 1:** **Input:** roads = \[\[0,1\],\[0,2\],\[0,3\]\], seats = 5 **Output:** 3 **Explanation:** - Representative1 goes directly to the capital with 1 liter of fuel. - Representative2 goes directly to the capital with 1 liter of fuel. - Representative3 goes directly to the capital with 1 liter of fuel. It costs 3 liters of fuel at minimum. It can be proven that 3 is the minimum number of liters of fuel needed. **Example 2:** **Input:** roads = \[\[3,1\],\[3,2\],\[1,0\],\[0,4\],\[0,5\],\[4,6\]\], seats = 2 **Output:** 7 **Explanation:** - Representative2 goes directly to city 3 with 1 liter of fuel. - Representative2 and representative3 go together to city 1 with 1 liter of fuel. - Representative2 and representative3 go together to the capital with 1 liter of fuel. - Representative1 goes directly to the capital with 1 liter of fuel. - Representative5 goes directly to the capital with 1 liter of fuel. - Representative6 goes directly to city 4 with 1 liter of fuel. - Representative4 and representative6 go together to the capital with 1 liter of fuel. It costs 7 liters of fuel at minimum. It can be proven that 7 is the minimum number of liters of fuel needed. **Example 3:** **Input:** roads = \[\], seats = 1 **Output:** 0 **Explanation:** No representatives need to travel to the capital city. **Constraints:** * `1 <= n <= 105` * `roads.length == n - 1` * `roads[i].length == 2` * `0 <= ai, bi < n` * `ai != bi` * `roads` represents a valid tree. * `1 <= seats <= 105`

BFS PYTHON WELL COMMENTED CODE

minimum-fuel-cost-to-report-to-the-capital

```\nclass Solution:\n #author : @PUDDINJK\n def minimumFuelCost(self, roads: List[List[int]], seats: int) -> int:\n \n #graph container\n graph = defaultdict(list)\n \n #to filter out leaf nodes on the graph\n degree = [0]* (len(roads)+1)\n \n #to count number of rep \n number_of_rep = [1]*(len(roads)+1)\n \n #builing graph using the following code\n for v, e in roads:\n graph[e].append(v)\n graph[v].append(e)\n degree[v]+=1\n degree[e]+=1\n \n #since we have to start from the child node we have to start with leaf node meaning nodes with one child\n queue = deque([node for node in range(len(degree)) if degree[node] == 1 and node != 0])\n \n fuel = 0\n \n \n while queue:\n node = queue.popleft()\n \n #calculate the number of coming cars here\n fuel+=ceil(number_of_rep[node]/seats)\n \n for vertex in graph[node]:\n degree[vertex]-=1\n \n #to calculate how many cars or representatives are coming from behind\n number_of_rep[vertex]+=number_of_rep[node]\n \n #if the vertex degree is 1 then there is a rep there if its more than one we assume we reached the capital\n if degree[vertex] == 1 and vertex != 0:\n queue.append(vertex)\n \n return fuel\n \n \n \n```

There is a tree (i.e., a connected, undirected graph with no cycles) structure country network consisting of `n` cities numbered from `0` to `n - 1` and exactly `n - 1` roads. The capital city is city `0`. You are given a 2D integer array `roads` where `roads[i] = [ai, bi]` denotes that there exists a **bidirectional road** connecting cities `ai` and `bi`. There is a meeting for the representatives of each city. The meeting is in the capital city. There is a car in each city. You are given an integer `seats` that indicates the number of seats in each car. A representative can use the car in their city to travel or change the car and ride with another representative. The cost of traveling between two cities is one liter of fuel. Return _the minimum number of liters of fuel to reach the capital city_. **Example 1:** **Input:** roads = \[\[0,1\],\[0,2\],\[0,3\]\], seats = 5 **Output:** 3 **Explanation:** - Representative1 goes directly to the capital with 1 liter of fuel. - Representative2 goes directly to the capital with 1 liter of fuel. - Representative3 goes directly to the capital with 1 liter of fuel. It costs 3 liters of fuel at minimum. It can be proven that 3 is the minimum number of liters of fuel needed. **Example 2:** **Input:** roads = \[\[3,1\],\[3,2\],\[1,0\],\[0,4\],\[0,5\],\[4,6\]\], seats = 2 **Output:** 7 **Explanation:** - Representative2 goes directly to city 3 with 1 liter of fuel. - Representative2 and representative3 go together to city 1 with 1 liter of fuel. - Representative2 and representative3 go together to the capital with 1 liter of fuel. - Representative1 goes directly to the capital with 1 liter of fuel. - Representative5 goes directly to the capital with 1 liter of fuel. - Representative6 goes directly to city 4 with 1 liter of fuel. - Representative4 and representative6 go together to the capital with 1 liter of fuel. It costs 7 liters of fuel at minimum. It can be proven that 7 is the minimum number of liters of fuel needed. **Example 3:** **Input:** roads = \[\], seats = 1 **Output:** 0 **Explanation:** No representatives need to travel to the capital city. **Constraints:** * `1 <= n <= 105` * `roads.length == n - 1` * `roads[i].length == 2` * `0 <= ai, bi < n` * `ai != bi` * `roads` represents a valid tree. * `1 <= seats <= 105`

Clean Codes🔥🔥|| Full Explanation✅|| DFS✅|| C++|| Java|| Python3

minimum-fuel-cost-to-report-to-the-capital

# Intuition :\n- Here we have to find the minimum fuel cost to transport people from a city (represented by node 0) to all other cities (represented by other nodes) in a road network.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach :\n- So we are using a depth-first search (DFS) algorithm to traverse the graph representing the road network. \n- The graph is represented as an array of linked lists, where each element in the array represents a node in the graph and the linked list contains the neighboring nodes of that node.\n- In the DFS function, the number of people in each city is calculated and stored in the people variable. This is done by starting from the current node (u) and visiting all its neighbors (v), and adding the number of people in each neighbor to people. \n- The number of cars needed to transport the people is then calculated by dividing the number of people by the number of seats in each car, rounded up to the nearest integer. \n- The cost is the number of cars needed, and it is added to the ans variable, which represents the total cost. The value of ans is returned as the result of the function.\n- The minimumFuelCost function takes in two parameters: roads, which is an array of roads represented as pairs of nodes, and seats, which is the number of seats in each car. \n- The function sets up the graph representation of the road network, calls the DFS function to calculate the cost, and returns the result.\n<!-- Describe your approach to solving the problem. -->\n# Explanation to Approach :\n- Our goal is to calculate the minimum amount of fuel needed to transport people from one city (city 0) to all the other cities in a road network. \n- So we are using a depth-first search algorithm to traverse the graph representation of the road network and counting the number of people in each city. \n- The number of cars needed to transport the people from one city to another is calculated by dividing the number of people by the number of seats in each car, rounded up to the nearest integer. \n- The total fuel cost is calculated as the sum of the number of cars needed to transport people between all cities.\n\n# Complexity\n- Time complexity : O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity : O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution.\uD83D\uDE0A\n```\n# Codes [C++ |Java |Python3] :\n```C++ []\nclass Solution {\n public:\n long long minimumFuelCost(vector<vector<int>>& roads, int seats) {\n long long ans = 0;\n vector<vector<int>> graph(roads.size() + 1);\n\n for (const vector<int>& road : roads) {\n const int u = road[0];\n const int v = road[1];\n graph[u].push_back(v);\n graph[v].push_back(u);\n }\n\n dfs(graph, 0, -1, seats, ans);\n return ans;\n }\n\n private:\n int dfs(const vector<vector<int>>& graph, int u, int prev, int seats,\n long long& ans) {\n int people = 1;\n for (const int v : graph[u]) {\n if (v == prev)\n continue;\n people += dfs(graph, v, u, seats, ans);\n }\n if (u > 0)\n // # of cars needed = ceil(people / seats)\n ans += (people + seats - 1) / seats;\n return people;\n }\n};\n```\n```Java []\nclass Solution {\n public long minimumFuelCost(int[][] roads, int seats) {\n List<Integer>[] graph = new List[roads.length + 1];\n\n for (int i = 0; i < graph.length; ++i)\n graph[i] = new ArrayList<>();\n\n for (int[] road : roads) {\n final int u = road[0];\n final int v = road[1];\n graph[u].add(v);\n graph[v].add(u);\n }\n\n dfs(graph, 0, -1, seats);\n return ans;\n }\n\n private long ans = 0;\n\n private int dfs(List<Integer>[] graph, int u, int prev, int seats) {\n int people = 1;\n for (final int v : graph[u]) {\n if (v == prev)\n continue;\n people += dfs(graph, v, u, seats);\n }\n if (u > 0)\n // # of cars needed = ceil(people / seats)\n ans += (people + seats - 1) / seats;\n return people;\n }\n}\n```\n```Python3 []\nclass Solution:\n def minimumFuelCost(self, roads: List[List[int]], seats: int) -> int:\n ans = 0\n graph = [[] for _ in range(len(roads) + 1)]\n\n for u, v in roads:\n graph[u].append(v)\n graph[v].append(u)\n\n def dfs(u: int, prev: int) -> int:\n nonlocal ans\n people = 1\n for v in graph[u]:\n if v == prev:\n continue\n people += dfs(v, u)\n if u > 0:\n # # of cars needed.\n ans += int(math.ceil(people / seats))\n return people\n\n dfs(0, -1)\n return ans\n```\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n\n

There is a tree (i.e., a connected, undirected graph with no cycles) structure country network consisting of `n` cities numbered from `0` to `n - 1` and exactly `n - 1` roads. The capital city is city `0`. You are given a 2D integer array `roads` where `roads[i] = [ai, bi]` denotes that there exists a **bidirectional road** connecting cities `ai` and `bi`. There is a meeting for the representatives of each city. The meeting is in the capital city. There is a car in each city. You are given an integer `seats` that indicates the number of seats in each car. A representative can use the car in their city to travel or change the car and ride with another representative. The cost of traveling between two cities is one liter of fuel. Return _the minimum number of liters of fuel to reach the capital city_. **Example 1:** **Input:** roads = \[\[0,1\],\[0,2\],\[0,3\]\], seats = 5 **Output:** 3 **Explanation:** - Representative1 goes directly to the capital with 1 liter of fuel. - Representative2 goes directly to the capital with 1 liter of fuel. - Representative3 goes directly to the capital with 1 liter of fuel. It costs 3 liters of fuel at minimum. It can be proven that 3 is the minimum number of liters of fuel needed. **Example 2:** **Input:** roads = \[\[3,1\],\[3,2\],\[1,0\],\[0,4\],\[0,5\],\[4,6\]\], seats = 2 **Output:** 7 **Explanation:** - Representative2 goes directly to city 3 with 1 liter of fuel. - Representative2 and representative3 go together to city 1 with 1 liter of fuel. - Representative2 and representative3 go together to the capital with 1 liter of fuel. - Representative1 goes directly to the capital with 1 liter of fuel. - Representative5 goes directly to the capital with 1 liter of fuel. - Representative6 goes directly to city 4 with 1 liter of fuel. - Representative4 and representative6 go together to the capital with 1 liter of fuel. It costs 7 liters of fuel at minimum. It can be proven that 7 is the minimum number of liters of fuel needed. **Example 3:** **Input:** roads = \[\], seats = 1 **Output:** 0 **Explanation:** No representatives need to travel to the capital city. **Constraints:** * `1 <= n <= 105` * `roads.length == n - 1` * `roads[i].length == 2` * `0 <= ai, bi < n` * `ai != bi` * `roads` represents a valid tree. * `1 <= seats <= 105`

[C++, Java, Python3] Simple DFS O(n)

minimum-fuel-cost-to-report-to-the-capital

# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe need to track the number of people that reach each node and divide that by the number of seats per car, this will tell us the number of cars required to take us to the node that is closer to node`0`\n\n# Approach\nDFS\n* Imagine you are at a leaf node, you move towards `0`. There will be only 1 person in the car (you)\n* Now let\'s say you\'re somewhere in the middle of the tree, with a car of size 5. You have 3 children nodes. Let\'s say each child node brings 1 car of 3 people. So a total of 3 * 3 = 9 people. Including you there are 10 people now. Now you have 3 cars from the child nodes and one car of your own. You actually need just 10 / 5 = 2 cars. You take 2 cars and move towards `0`\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n\n# Code\n**Python 3**\n```\n def minimumFuelCost(self, roads: List[List[int]], seats: int) -> int:\n graph = defaultdict(list)\n for x, y in roads:\n graph[x].append(y)\n graph[y].append(x)\n self.ans = 0\n \n def dfs(i, prev, people = 1):\n for x in graph[i]:\n if x == prev: continue\n people += dfs(x, i)\n self.ans += (int(ceil(people / seats)) if i else 0)\n return people\n \n dfs(0, 0)\n return self.ans\n```\n\n**C++**\n```\nlong long ans = 0; int s;\nlong long minimumFuelCost(vector<vector<int>>& roads, int seats) {\n vector<vector<int>> graph(roads.size() + 1); s = seats;\n for (vector<int>& r: roads) {\n graph[r[0]].push_back(r[1]);\n graph[r[1]].push_back(r[0]);\n }\n dfs(0, 0, graph);\n return ans;\n}\nint dfs(int i, int prev, vector<vector<int>>& graph, int people = 1) {\n for (int& x: graph[i]) {\n if (x == prev) continue;\n people += dfs(x, i, graph);\n }\n if (i != 0) ans += (people + s - 1) / s;\n return people;\n}\n```\n\n**Java**\n```\nlong ans = 0; int s;\npublic long minimumFuelCost(int[][] roads, int seats) {\n List<List<Integer>> graph = new ArrayList(); s = seats;\n for (int i = 0; i < roads.length + 1; i++) graph.add(new ArrayList());\n for (int[] r: roads) {\n graph.get(r[0]).add(r[1]);\n graph.get(r[1]).add(r[0]);\n }\n dfs(0, 0, graph);\n return ans;\n}\nprivate int dfs(int i, int prev, List<List<Integer>> graph) {\n int people = 1;\n for (int x: graph.get(i)) {\n if (x == prev) continue;\n people += dfs(x, i, graph);\n }\n if (i != 0) ans += (people + s - 1) / s;\n return people;\n}\n```

There is a tree (i.e., a connected, undirected graph with no cycles) structure country network consisting of `n` cities numbered from `0` to `n - 1` and exactly `n - 1` roads. The capital city is city `0`. You are given a 2D integer array `roads` where `roads[i] = [ai, bi]` denotes that there exists a **bidirectional road** connecting cities `ai` and `bi`. There is a meeting for the representatives of each city. The meeting is in the capital city. There is a car in each city. You are given an integer `seats` that indicates the number of seats in each car. A representative can use the car in their city to travel or change the car and ride with another representative. The cost of traveling between two cities is one liter of fuel. Return _the minimum number of liters of fuel to reach the capital city_. **Example 1:** **Input:** roads = \[\[0,1\],\[0,2\],\[0,3\]\], seats = 5 **Output:** 3 **Explanation:** - Representative1 goes directly to the capital with 1 liter of fuel. - Representative2 goes directly to the capital with 1 liter of fuel. - Representative3 goes directly to the capital with 1 liter of fuel. It costs 3 liters of fuel at minimum. It can be proven that 3 is the minimum number of liters of fuel needed. **Example 2:** **Input:** roads = \[\[3,1\],\[3,2\],\[1,0\],\[0,4\],\[0,5\],\[4,6\]\], seats = 2 **Output:** 7 **Explanation:** - Representative2 goes directly to city 3 with 1 liter of fuel. - Representative2 and representative3 go together to city 1 with 1 liter of fuel. - Representative2 and representative3 go together to the capital with 1 liter of fuel. - Representative1 goes directly to the capital with 1 liter of fuel. - Representative5 goes directly to the capital with 1 liter of fuel. - Representative6 goes directly to city 4 with 1 liter of fuel. - Representative4 and representative6 go together to the capital with 1 liter of fuel. It costs 7 liters of fuel at minimum. It can be proven that 7 is the minimum number of liters of fuel needed. **Example 3:** **Input:** roads = \[\], seats = 1 **Output:** 0 **Explanation:** No representatives need to travel to the capital city. **Constraints:** * `1 <= n <= 105` * `roads.length == n - 1` * `roads[i].length == 2` * `0 <= ai, bi < n` * `ai != bi` * `roads` represents a valid tree. * `1 <= seats <= 105`

Python short and clean. DFS. Functional Programming.

minimum-fuel-cost-to-report-to-the-capital

# Approach\n1. Define a function `min_cost` that given a subtree rooted at `node` computes the number of people in the subtree, say `total_people`, and the minimum fuel cost to gather them all at `node`, say `total_cost`.\n\n2. To compute the `(total_cost, total_people)` from `node`, recursively call `min_cost` on each `child`.\n\n3. Say for each `child`, `c` and `t` are the cost and people, then\n `total_people += p`, current number of people in `child`\n `total_cost += c + ceil(c / seats)`, current cost + cost to travel from `child` to `node`.\n\n4. Return `total_cost`.\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\nwhere `n is the number of cities`.\n\n# Code\nImperative: Iterative `min_cost` function.\n```python\nclass Solution:\n def minimumFuelCost(self, roads: list[list[int]], seats_: int) -> int:\n T = Hashable\n Graph = Mapping[T, Iterable[T]]\n\n def min_cost(graph: Graph, node: T, seats: int, parent: T | None = None) -> tuple[int, int]:\n total_cost, total_people = 0, 1\n for child in graph[node]:\n if child == parent: continue\n c, p = min_cost(graph, child, seats, node)\n total_people += p\n total_cost += c + ceil(p / seats)\n return total_cost, total_people\n \n g = defaultdict(list)\n for u, v in roads: g[u].append(v); g[v].append(u)\n\n return min_cost(g, 0, seats_)[0]\n\n\n```\n\nFunctional: 1-liner `min_cost` function.\n```python\nclass Solution:\n def minimumFuelCost(self, roads: list[list[int]], seats_: int) -> int:\n T = Hashable\n Graph = Mapping[T, Iterable[T]]\n\n def min_cost(graph: Graph, node: T, seats: int, parent: T | None = None) -> tuple[int, int]:\n return reduce(\n lambda a, x: (a[0] + x[0] + ceil(x[1] / seats), a[1] + x[1]), \n (min_cost(graph, child, seats, node) for child in graph[node] if child != parent),\n (0, 1), # (total_cost, total_people)\n )\n \n g = defaultdict(list)\n for u, v in roads: g[u].append(v); g[v].append(u)\n\n return min_cost(g, 0, seats_)[0]\n\n\n```

There is a tree (i.e., a connected, undirected graph with no cycles) structure country network consisting of `n` cities numbered from `0` to `n - 1` and exactly `n - 1` roads. The capital city is city `0`. You are given a 2D integer array `roads` where `roads[i] = [ai, bi]` denotes that there exists a **bidirectional road** connecting cities `ai` and `bi`. There is a meeting for the representatives of each city. The meeting is in the capital city. There is a car in each city. You are given an integer `seats` that indicates the number of seats in each car. A representative can use the car in their city to travel or change the car and ride with another representative. The cost of traveling between two cities is one liter of fuel. Return _the minimum number of liters of fuel to reach the capital city_. **Example 1:** **Input:** roads = \[\[0,1\],\[0,2\],\[0,3\]\], seats = 5 **Output:** 3 **Explanation:** - Representative1 goes directly to the capital with 1 liter of fuel. - Representative2 goes directly to the capital with 1 liter of fuel. - Representative3 goes directly to the capital with 1 liter of fuel. It costs 3 liters of fuel at minimum. It can be proven that 3 is the minimum number of liters of fuel needed. **Example 2:** **Input:** roads = \[\[3,1\],\[3,2\],\[1,0\],\[0,4\],\[0,5\],\[4,6\]\], seats = 2 **Output:** 7 **Explanation:** - Representative2 goes directly to city 3 with 1 liter of fuel. - Representative2 and representative3 go together to city 1 with 1 liter of fuel. - Representative2 and representative3 go together to the capital with 1 liter of fuel. - Representative1 goes directly to the capital with 1 liter of fuel. - Representative5 goes directly to the capital with 1 liter of fuel. - Representative6 goes directly to city 4 with 1 liter of fuel. - Representative4 and representative6 go together to the capital with 1 liter of fuel. It costs 7 liters of fuel at minimum. It can be proven that 7 is the minimum number of liters of fuel needed. **Example 3:** **Input:** roads = \[\], seats = 1 **Output:** 0 **Explanation:** No representatives need to travel to the capital city. **Constraints:** * `1 <= n <= 105` * `roads.length == n - 1` * `roads[i].length == 2` * `0 <= ai, bi < n` * `ai != bi` * `roads` represents a valid tree. * `1 <= seats <= 105`

Python solution

minimum-fuel-cost-to-report-to-the-capital

\n\n# Code\n```\nclass Solution:\n def minimumFuelCost(self, roads: List[List[int]], seats: int) -> int:\n graph=defaultdict(list)\n \n for i,j in roads:\n graph[i].append(j)\n graph[j].append(i)\n\n print(graph)\n \n \n def dfs(node,parent):\n nonlocal res\n \n passengers=0\n\n for child in graph[node]:\n if child!=parent:\n p=dfs(child,node)\n passengers+=p\n res += int(ceil(p/seats))\n return passengers+1\n\n res = 0\n dfs(0,-1)\n return res\n \n\n\n```

There is a tree (i.e., a connected, undirected graph with no cycles) structure country network consisting of `n` cities numbered from `0` to `n - 1` and exactly `n - 1` roads. The capital city is city `0`. You are given a 2D integer array `roads` where `roads[i] = [ai, bi]` denotes that there exists a **bidirectional road** connecting cities `ai` and `bi`. There is a meeting for the representatives of each city. The meeting is in the capital city. There is a car in each city. You are given an integer `seats` that indicates the number of seats in each car. A representative can use the car in their city to travel or change the car and ride with another representative. The cost of traveling between two cities is one liter of fuel. Return _the minimum number of liters of fuel to reach the capital city_. **Example 1:** **Input:** roads = \[\[0,1\],\[0,2\],\[0,3\]\], seats = 5 **Output:** 3 **Explanation:** - Representative1 goes directly to the capital with 1 liter of fuel. - Representative2 goes directly to the capital with 1 liter of fuel. - Representative3 goes directly to the capital with 1 liter of fuel. It costs 3 liters of fuel at minimum. It can be proven that 3 is the minimum number of liters of fuel needed. **Example 2:** **Input:** roads = \[\[3,1\],\[3,2\],\[1,0\],\[0,4\],\[0,5\],\[4,6\]\], seats = 2 **Output:** 7 **Explanation:** - Representative2 goes directly to city 3 with 1 liter of fuel. - Representative2 and representative3 go together to city 1 with 1 liter of fuel. - Representative2 and representative3 go together to the capital with 1 liter of fuel. - Representative1 goes directly to the capital with 1 liter of fuel. - Representative5 goes directly to the capital with 1 liter of fuel. - Representative6 goes directly to city 4 with 1 liter of fuel. - Representative4 and representative6 go together to the capital with 1 liter of fuel. It costs 7 liters of fuel at minimum. It can be proven that 7 is the minimum number of liters of fuel needed. **Example 3:** **Input:** roads = \[\], seats = 1 **Output:** 0 **Explanation:** No representatives need to travel to the capital city. **Constraints:** * `1 <= n <= 105` * `roads.length == n - 1` * `roads[i].length == 2` * `0 <= ai, bi < n` * `ai != bi` * `roads` represents a valid tree. * `1 <= seats <= 105`

Python || Depth-First Search || Easy To Understand 🔥

minimum-fuel-cost-to-report-to-the-capital

# Code\n```\nclass Solution: \n def minimumFuelCost(self, roads: List[List[int]], seats: int) -> int:\n def dfs(i, prev, people = 1):\n for x in graph[i]:\n if x == prev:\n continue\n people += dfs(x, i)\n if i:\n self.ans += (int(ceil(people / seats)))\n else:\n self.ans += 0\n return people\n graph = defaultdict(list)\n for x, y in roads:\n graph[x].append(y)\n graph[y].append(x)\n self.ans = 0\n dfs(0, 0)\n return self.ans\n```

There is a tree (i.e., a connected, undirected graph with no cycles) structure country network consisting of `n` cities numbered from `0` to `n - 1` and exactly `n - 1` roads. The capital city is city `0`. You are given a 2D integer array `roads` where `roads[i] = [ai, bi]` denotes that there exists a **bidirectional road** connecting cities `ai` and `bi`. There is a meeting for the representatives of each city. The meeting is in the capital city. There is a car in each city. You are given an integer `seats` that indicates the number of seats in each car. A representative can use the car in their city to travel or change the car and ride with another representative. The cost of traveling between two cities is one liter of fuel. Return _the minimum number of liters of fuel to reach the capital city_. **Example 1:** **Input:** roads = \[\[0,1\],\[0,2\],\[0,3\]\], seats = 5 **Output:** 3 **Explanation:** - Representative1 goes directly to the capital with 1 liter of fuel. - Representative2 goes directly to the capital with 1 liter of fuel. - Representative3 goes directly to the capital with 1 liter of fuel. It costs 3 liters of fuel at minimum. It can be proven that 3 is the minimum number of liters of fuel needed. **Example 2:** **Input:** roads = \[\[3,1\],\[3,2\],\[1,0\],\[0,4\],\[0,5\],\[4,6\]\], seats = 2 **Output:** 7 **Explanation:** - Representative2 goes directly to city 3 with 1 liter of fuel. - Representative2 and representative3 go together to city 1 with 1 liter of fuel. - Representative2 and representative3 go together to the capital with 1 liter of fuel. - Representative1 goes directly to the capital with 1 liter of fuel. - Representative5 goes directly to the capital with 1 liter of fuel. - Representative6 goes directly to city 4 with 1 liter of fuel. - Representative4 and representative6 go together to the capital with 1 liter of fuel. It costs 7 liters of fuel at minimum. It can be proven that 7 is the minimum number of liters of fuel needed. **Example 3:** **Input:** roads = \[\], seats = 1 **Output:** 0 **Explanation:** No representatives need to travel to the capital city. **Constraints:** * `1 <= n <= 105` * `roads.length == n - 1` * `roads[i].length == 2` * `0 <= ai, bi < n` * `ai != bi` * `roads` represents a valid tree. * `1 <= seats <= 105`

[C++, Python] Short DP explained

number-of-beautiful-partitions

# Intuition\nWe will have to use dynamic programming because there are overlapping subproblems. n^3 dp will fail due to time constraints. To use n^2 dp we will keep a flag `at_start` which means that the substring starts at this point and as per the question the start should be prime.\n\n# Approach\nDP\n* The DP state is defined by `i`, `at_start` and `k`. `i` ranges from 0 to length of s, `at_start` is true of false and `k` ranges from k to 0. Hence time complexity = (length of s) * 2 * k\n* If we reach the end of string (i == n) return k == 0 which means that we have exactly `k` substrings\n* If `i > n` or `k` is prematurely 0 or s[i] is not a prime number and we are at start of string we return 0\n* If s[i] is a prime number and we are at start of string move minLength characters ahead\n* If s[i] is a prime number and we are *not* at start of string return the (i + 1) state because we cannot end the substring here\n* If s[i] is not prime we can either set this as end of current substring or continue making the current substring longer. We sum both these cases and return the result\n\n# Complexity\n- Time complexity: O(nk)\n\n- Space complexity: O(nk)\n\n# Code\n**Python3**\n```\ndef beautifulPartitions(self, s: str, k: int, minLength: int) -> int:\n n, primes, mod = len(s), set(\'2357\'), (10 ** 9) + 7\n @cache\n def dp(i, at_start, k):\n if i == n: return int(k == 0)\n if i > n or k == 0 or s[i] not in primes and at_start: return 0\n if s[i] in primes:\n if at_start: return dp(i + minLength - 1, False, k)\n else: return dp(i + 1, False, k)\n return (dp(i + 1, True, k - 1) + dp(i + 1, False, k)) % mod\n return dp(0, True, k)\n```\n\n**C++**\n```\nunordered_set<char> prime {\'2\', \'3\', \'5\', \'7\'};\nint mod = 1e9 + 7, minLength, dp[1001][2][1001]; \nint beautifulPartitions(string s, int k, int ml) {\n minLength = ml;\n memset(dp, -1, sizeof dp);\n return dfs(0, true, k, s);\n}\nint dfs(int i, bool at_start, int k, string& s, int ans = 0) {\n if (i == s.size()) return k == 0;\n if (i > s.size() || k == 0 || !prime.count(s[i]) && at_start) return 0;\n if (dp[i][at_start][k] != -1) return dp[i][at_start][k];\n if (prime.count(s[i])) {\n if (at_start) ans = dfs(i + minLength - 1, false, k, s);\n else ans = dfs(i + 1, false, k, s);\n }\n else ans = (dfs(i + 1, true, k - 1, s) + dfs(i + 1, false, k, s)) % mod;\n return dp[i][at_start][k] = ans;\n}\n```\n

You are given a string `s` that consists of the digits `'1'` to `'9'` and two integers `k` and `minLength`. A partition of `s` is called **beautiful** if: * `s` is partitioned into `k` non-intersecting substrings. * Each substring has a length of **at least** `minLength`. * Each substring starts with a **prime** digit and ends with a **non-prime** digit. Prime digits are `'2'`, `'3'`, `'5'`, and `'7'`, and the rest of the digits are non-prime. Return _the number of **beautiful** partitions of_ `s`. Since the answer may be very large, return it **modulo** `109 + 7`. A **substring** is a contiguous sequence of characters within a string. **Example 1:** **Input:** s = "23542185131 ", k = 3, minLength = 2 **Output:** 3 **Explanation:** There exists three ways to create a beautiful partition: "2354 | 218 | 5131 " "2354 | 21851 | 31 " "2354218 | 51 | 31 " **Example 2:** **Input:** s = "23542185131 ", k = 3, minLength = 3 **Output:** 1 **Explanation:** There exists one way to create a beautiful partition: "2354 | 218 | 5131 ". **Example 3:** **Input:** s = "3312958 ", k = 3, minLength = 1 **Output:** 1 **Explanation:** There exists one way to create a beautiful partition: "331 | 29 | 58 ". **Constraints:** * `1 <= k, minLength <= s.length <= 1000` * `s` consists of the digits `'1'` to `'9'`.

[Python] Top down DP - Clean & Concise - O(N * K)

number-of-beautiful-partitions

# Intuition\nFor each position, we have 2 options:\n- Do not split on that position.\n- Split on that position if we can (`s[i]` is prime, and `s[i - 1]` is non-prime).\nNote that, after the split, we need to advance `i` by `minLength`.\n\n# Complexity\n- Time complexity: `O(N * K)`, where `N <= 1000` is length of string `s`, `K <= N`\n- Space complexity: `O(N * K)`\n\n# Code\n```\nclass Solution:\n def beautifulPartitions(self, s: str, k: int, minLength: int) -> int:\n n = len(s)\n MOD = 10**9 + 7\n\n def isPrime(c):\n return c in [\'2\', \'3\', \'5\', \'7\']\n\n @lru_cache(None)\n def dp(i, k):\n if k == 0 and i <= n:\n return 1\n if i >= n:\n return 0\n\n ans = dp(i+1, k) # Skip\n if isPrime(s[i]) and not isPrime(s[i-1]): # Split\n ans += dp(i+minLength, k-1)\n return ans % MOD\n\n if not isPrime(s[0]) or isPrime(s[-1]): return 0\n\n return dp(minLength, k-1)\n```

You are given a string `s` that consists of the digits `'1'` to `'9'` and two integers `k` and `minLength`. A partition of `s` is called **beautiful** if: * `s` is partitioned into `k` non-intersecting substrings. * Each substring has a length of **at least** `minLength`. * Each substring starts with a **prime** digit and ends with a **non-prime** digit. Prime digits are `'2'`, `'3'`, `'5'`, and `'7'`, and the rest of the digits are non-prime. Return _the number of **beautiful** partitions of_ `s`. Since the answer may be very large, return it **modulo** `109 + 7`. A **substring** is a contiguous sequence of characters within a string. **Example 1:** **Input:** s = "23542185131 ", k = 3, minLength = 2 **Output:** 3 **Explanation:** There exists three ways to create a beautiful partition: "2354 | 218 | 5131 " "2354 | 21851 | 31 " "2354218 | 51 | 31 " **Example 2:** **Input:** s = "23542185131 ", k = 3, minLength = 3 **Output:** 1 **Explanation:** There exists one way to create a beautiful partition: "2354 | 218 | 5131 ". **Example 3:** **Input:** s = "3312958 ", k = 3, minLength = 1 **Output:** 1 **Explanation:** There exists one way to create a beautiful partition: "331 | 29 | 58 ". **Constraints:** * `1 <= k, minLength <= s.length <= 1000` * `s` consists of the digits `'1'` to `'9'`.

Python simple DP with optimization

number-of-beautiful-partitions

\n```\nclass Solution:\n def beautifulPartitions(self, s: str, k: int, minLength: int) -> int:\n n = len(s)\n primes = [\'2\', \'3\', \'5\', \'7\']\n \n # pruning\n if k * minLength > n or s[0] not in primes or s[-1] in primes:\n return 0\n \n # posible starting indexes of a new partition\n ids = [0]\n for i in range(n-1):\n if s[i] not in primes and s[i+1] in primes:\n ids.append(i+1)\n m = len(ids)\n\n @cache\n # dp(i, kk) means number of ways to partition s[ids[i]:n] into kk partitions\n def dp(i, kk):\n \n # kk==1: last remaining partition, needs to have length >= l\n if kk == 1:\n return 1 if ids[i]+minLength-1 <= n-1 else 0\n res = 0\n \n # iterate possible starting index of next partition\n for j in range(i+1, m-kk+2):\n if ids[j]-ids[i] >= minLength:\n res += dp(j, kk-1)\n \n return res % (10**9+7)\n \n return dp(0, k)\n \n```

You are given a string `s` that consists of the digits `'1'` to `'9'` and two integers `k` and `minLength`. A partition of `s` is called **beautiful** if: * `s` is partitioned into `k` non-intersecting substrings. * Each substring has a length of **at least** `minLength`. * Each substring starts with a **prime** digit and ends with a **non-prime** digit. Prime digits are `'2'`, `'3'`, `'5'`, and `'7'`, and the rest of the digits are non-prime. Return _the number of **beautiful** partitions of_ `s`. Since the answer may be very large, return it **modulo** `109 + 7`. A **substring** is a contiguous sequence of characters within a string. **Example 1:** **Input:** s = "23542185131 ", k = 3, minLength = 2 **Output:** 3 **Explanation:** There exists three ways to create a beautiful partition: "2354 | 218 | 5131 " "2354 | 21851 | 31 " "2354218 | 51 | 31 " **Example 2:** **Input:** s = "23542185131 ", k = 3, minLength = 3 **Output:** 1 **Explanation:** There exists one way to create a beautiful partition: "2354 | 218 | 5131 ". **Example 3:** **Input:** s = "3312958 ", k = 3, minLength = 1 **Output:** 1 **Explanation:** There exists one way to create a beautiful partition: "331 | 29 | 58 ". **Constraints:** * `1 <= k, minLength <= s.length <= 1000` * `s` consists of the digits `'1'` to `'9'`.

Java, Python 3, C++ || Iterative 1D DP || Easy to Understand || Runtime 22ms Beats 100%

number-of-beautiful-partitions

First, we need to verify 3 special cases:\n```\nif (!isprime(s.charAt(0)) || isprime(s.charAt(s.length()-1))){return 0;}\nif (s.length()<minLength){return 0;}\nif (k==1){return 1;}\n```\nNext, we find all the indexes which can be starts of partitions (excluding 0 as 0 is a fixed one):\n```\n/* array of indexes which can be starts of partitions */\nint[] primeid = new int[s.length()];\nint ln = 0; /* length of primeid */\nfor (int i=minLength;i<=s.length()-minLength;i++){\n if (isprime(s.charAt(i))&&!isprime(s.charAt(i-1))){\n primeid[ln]=i;\n ln++;\n }\n }\n```\nThe original problem is then reduced to finding the number of $K=(k-1)$ combinations of the indexes above where the difference between each indexes pair $>=minLength$. Bottom up dynamic programming can be used to solve this using two 1D arrays. Note that we have already verify the special case $k==1$, thus we now have $K=k-1>=1$ or the base case is $K=1$.\n```\nint[] dp1 = new int[ln]; /* number of satisfied K combinations */\nint[] dp = new int[ln]; /* number of satisfied K+1 combinations */\n```\n$dp1[i]$ is the number of satisfied $K$ combinations using $primeid[0] ... primeid[i]$. \n$dp[i]$ is the number of satisfied $K+1$ combinations using $primeid[0] ... primeid[i]$.\n\nBase case $K=1$:\n```\ndp1[i]=i+1; /* length of primeid[:i+1] */\n```\nDP relation: $dp[i]$ is the sum of\n+ $dp[i-1]$, i.e. the number of $K+1$ combinations using $primeid[0] ... primeid[i-1]$,\n+ and $dp1[j]$ where $j$ is the largest such that $primeid[i]-primeid[j]>=minLength$, i.e. the number of $K$ combinations using $primeid[0] ... primeid[j]$ where $primeid[i]$ can be further combined to form satisfied $K+1$ combinations.\n \n# Java\n```\n/* Runtime 22 ms Beats 100%, Memory 41.9 MB Beats 100% */\nclass Solution {\n public boolean isprime(char c) {\n return c==\'2\'||c==\'3\'||c==\'5\'||c==\'7\';\n }\n public int beautifulPartitions(String s, int k, int minLength) {\n int n = s.length();\n if (!isprime(s.charAt(0)) || isprime(s.charAt(n-1))){return 0;}\n if (n<minLength){return 0;}\n if (k==1){return 1;}\n int[] primeid = new int[n];\n int ln = 0;\n for (int i=minLength;i<=n-minLength;i++){\n if (isprime(s.charAt(i))&&!isprime(s.charAt(i-1))){\n primeid[ln]=i;\n ln++;\n }\n }\n int mod = 1000000007;\n if (ln<k-1){return 0;}\n int[] dp1 = new int[ln];\n int[] dp = new int[ln];\n for (int i=0;i<ln;i++){\n dp1[i]=i+1;\n dp[i]=0;\n }\n for (int ik=2;ik<k;ik++){\n for (int i=ik-1;i<ln;i++){\n dp[i] = dp[i-1];\n for (int j=i-1;j>-1;j--){\n if (primeid[i]-primeid[j]>=minLength){\n dp[i] = (dp[i]+dp1[j])%mod;\n break;\n }\n }\n }\n for (int i=0;i<ln;i++){\n dp1[i]=dp[i];\n dp[i]=0;\n }\n }\n return dp1[ln-1]; \n }\n}\n```\n# Python 3\n```\n# Runtime 458 ms Beats 100%, Memory 14.1 MB Beats 100%\nclass Solution:\n def beautifulPartitions(self, s, k, minLength):\n prime = {\'2\',\'3\',\'5\',\'7\'}\n if s[0] not in prime or s[-1] in prime:\n return 0\n n = len(s)\n if n<minLength:\n return 0\n if k==1:\n return 1\n primeid = []\n for i in range(minLength,n-minLength+1):\n if s[i] in prime and s[i-1] not in prime:\n primeid.append(i)\n mod, ln = 1000000007, len(primeid)\n if ln<k-1: return 0\n dp1 = [i+1 for i in range(ln)] \n dp = [0]*ln\n for ik in range(2,k):\n for i in range(ik-1,ln):\n dp[i] = dp[i-1]\n for j in range(i-1,-1,-1):\n if primeid[i]-primeid[j]>=minLength:\n dp[i] = (dp[i]+dp1[j])%mod\n break\n dp1 = dp[:]\n dp = [0]*ln\n return dp1[-1]\n```\n# C++\n```\n// Runtime 24 ms Beats 100%, Memory 6.6 MB Beats 100%\nclass Solution {\npublic:\n bool isprime(char c) {\n return c==\'2\'||c==\'3\'||c==\'5\'||c==\'7\';\n }\n int beautifulPartitions(string s, int k, int minLength) {\n int n = s.size();\n if (!isprime(s[0]) || isprime(s[n-1])){return 0;}\n if (n<minLength){return 0;}\n if (k==1){return 1;}\n vector<int> primeid;\n for (int i=minLength;i<=n-minLength;i++){\n if (isprime(s[i])&&!isprime(s[i-1])){\n primeid.push_back(i);\n }\n }\n int mod = 1000000007;\n int ln = primeid.size();\n if (ln<k-1){return 0;}\n int dp1[ln], dp[ln];\n for (int i=0;i<ln;i++){\n dp1[i]=i+1;\n dp[i]=0;\n }\n for (int ik=2;ik<k;ik++){\n for (int i=ik-1;i<ln;i++){\n dp[i] = dp[i-1];\n for (int j=i-1;j>-1;j--){\n if (primeid[i]-primeid[j]>=minLength){\n dp[i] = (dp[i]+dp1[j])%mod;\n break;\n }\n }\n }\n for (int i=0;i<ln;i++){\n dp1[i]=dp[i];\n dp[i]=0;\n }\n }\n return dp1[ln-1]; \n }\n};\n```

You are given a string `s` that consists of the digits `'1'` to `'9'` and two integers `k` and `minLength`. A partition of `s` is called **beautiful** if: * `s` is partitioned into `k` non-intersecting substrings. * Each substring has a length of **at least** `minLength`. * Each substring starts with a **prime** digit and ends with a **non-prime** digit. Prime digits are `'2'`, `'3'`, `'5'`, and `'7'`, and the rest of the digits are non-prime. Return _the number of **beautiful** partitions of_ `s`. Since the answer may be very large, return it **modulo** `109 + 7`. A **substring** is a contiguous sequence of characters within a string. **Example 1:** **Input:** s = "23542185131 ", k = 3, minLength = 2 **Output:** 3 **Explanation:** There exists three ways to create a beautiful partition: "2354 | 218 | 5131 " "2354 | 21851 | 31 " "2354218 | 51 | 31 " **Example 2:** **Input:** s = "23542185131 ", k = 3, minLength = 3 **Output:** 1 **Explanation:** There exists one way to create a beautiful partition: "2354 | 218 | 5131 ". **Example 3:** **Input:** s = "3312958 ", k = 3, minLength = 1 **Output:** 1 **Explanation:** There exists one way to create a beautiful partition: "331 | 29 | 58 ". **Constraints:** * `1 <= k, minLength <= s.length <= 1000` * `s` consists of the digits `'1'` to `'9'`.

DP Approach | Commented and Explained with Example Walkthrough

number-of-beautiful-partitions

# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nConsider the first example provided \nInput: s = "23542185131", k = 3, minLength = 2\nOutput: 3\nExplanation: There exists three ways to create a beautiful partition:\n"2354 | 218 | 5131"\n"2354 | 21851 | 31"\n"2354218 | 51 | 31"\n\nNot very intuitive where to start at first is it? \nTo get around that, let\'s set some edge cases based on the conditions provided. We know that \n- string consists of 1-9 as letters \n- two integers k and minLength\n- a beautiful partition is a partition that \n - is a split into k non-intersecting substrings \n - has a length of minLength at least \n - all substrings are contiguous \n - each substring starts with a 2, 3, 5, or 7 \n - each substring ends with a 1, 4, 6, 8 or 9 \n\nFrom these we can derive a few useful insights \n- minLength must always actually be 2 or greater, since a minLength of 1 is not possible considering the start and stop states of a substring \n- if our string starts with factor or ends with a prime, it is not possible to generate ANY partitions \n- if our minLength * num_segments is greater than our string length, it is also not possible to generate ANY partitions \n\nWith these in mind we can start to bind the problem. \nOur first binding approach should be to consider the points from which segments can originate \nAll segments must start at prime value. So, we can make a listing of each position from which these can start, which we call is_prime_value \n\nAlright, let\'s do our example walkthrough \nOur is_prime_value array looks like [T, T, T, F, T, F, F, T, F, T, F]\nFor segment_i in range 3 \n- at segment_i = 0, valid_start_partitions = 0, segment_start = 1, segment_stop = 7 \n - so for segment index in range 1 to 6 inclusive \n - dp index is then in range -1 to 4 inclusive \n - so we look at prime indices for 0 to 5 inclusive \n - for segment index = 1, dp index = -1, \n - valid start partitions is incremented by previous dp array at -1, now equals 1 \n - for segment index = 2, dp index = 0 \n - nothing \n - for segment index = 3, dp index = 1 \n - current dp array at 3 = 1\n - for segment index = 4, dp index = 2 \n - nothing \n - for segment index = 5, dp index = 3 \n - current dp array at 5 = 1 \n - for segment index = 6, dp index = 4 \n - current dp array at 6 = 1 \n - at end,current_dp_array= [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1] \n - at end,previous_dp_array=[0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0]\n - this shows our catching of the 2354, 21851, and 2354218\n- at segment_i = 1, valid start partitions = 0, segment start = 3, segment stop = 9\n - so for segment index in range 3 to 8 inclusive \n - dp index is then in range 1 to 6 inclusive \n - so we look at prime indices for 2 to 7 inclusive \n - for segment index = 3, dp index = 1 \n - nothing\n - for segment index = 4, dp index = 2 \n - nothing \n - for segment index = 5, dp index = 3 \n - valid start partitions is now 1 \n - current dp array at 5 is now 1 \n - for segment index = 6, dp index = 4 \n - current dp array at 6 is now 1 \n - for segment index = 7, dp index = 5 \n - nothing \n - for segment index = 8, dp index = 6 \n - valid start positions is now 2 \n - current dp array at 8 is now 2 \n - at end, current_dp_array=[0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0]\n - at end,previous_dp_array=[0, 0, 0, 0, 0, 1, 1, 0, 2, 0, 1]\n- at segment_i = 2, valid start partitions = 0, segment start = 5, segment stop = 11 \n - so for segment index in range 5 to 10 inclusive \n - dp index is then in range 3 to 8 inclusive \n - so we look at prime indices for 4 to 9 inclusive \n - for segment index = 5, dp index = 3 \n - current dp array at 5 is 0 \n - for segment index = 6, dp index = 4 \n - current dp array at 6 is 0 \n - for segment index = 7, dp index = 5 \n - nothing \n - for segment index = 8, dp index = 6 \n - valid start positions now 1 \n - current dp array at 8 is now 1 \n - for segment index = 9, dp index = 7 \n - nothing \n - for segment index = 10, dp index = 8 \n - valid start positions is now 3 \n - current dp array at 10 is 3 \n - at end, current_dp_array= [0, 0, 0, 0, 0, 1, 1, 0, 2, 0, 1]\n - at end, previous_dp_array=[0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 3]\n\nSo we return 3 \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSet up your mod, min length, length of s, primes, is prime value array conditions, and pass your default edge cases\nThen set up your previous dp array and your current dp array \nSet previous dp array at -1 to 1 (this brings in the at least one valid partition, which may or may not be the case actually) \nFor each segment consideration in size k \n- find the start and stop of this segment partition \n- set the valid start partitions in this segmentation location to 0 \n- loop over segment indexing for the end of the segment from start to stop \n - as you do, the dp index is minLength back from the segment index \n - if we have a prime value at dp index + 1 \n - we need to increment valid start positions by the prior dp array at the dp index \n - if we have a cofactor value at segment index \n - we need to set the current dp array at the segment index to the number of current valid start partitions modular mod \n- at the end of considering a current segment, set the current dp array and the previous dp array to swaps of each other respectively \n\nWhen done our previous dp array at -1 has the answer. Return it modularly \n\n# Complexity\n- Time complexity : O(k * s\')\n - We consider k num segments \n - each of which is size minLength to maximal length, where maximal length is the even division of s by minLength or k, whichever is greater, plus any remainder. This is a constant factor of size s\' \n - Total is k * s\' \n\n- Space complexity: O(s)\n - We use three arrays of size s \n\n# Code\n```\nclass Solution:\n def beautifulPartitions(self, s: str, k: int, minLength: int) -> int:\n mod = 1_000_000_007\n # force substrings of size 2 to account for the above criterion \n minLength = 2 if minLength < 2 else minLength\n sL = len(s) \n primes = \'2357\'\n is_prime_value = [char in primes for char in s]\n # if we cannot make the segments, or the segments as needed cannot be made, return 0 \n if is_prime_value[0] == False or is_prime_value[-1] == True or minLength * k > sL : \n return 0 \n else : \n # build a dynamic programming array where the value at the ith index is the solution of the problem for the prefix of the string ending at index i \n # then the answer for the problem will be at the length of the string - 1 of the dynamic programming array \n # the transitions to this can be found as follows by first setting the appropriately sized arrays of 0s \n previous_dp_array = [0] * sL \n current_dp_array = [0] * sL\n # set last index in previous dp array to 1 for first iteration \n # this will be overwritten in subsequent iterations, so it\'s setting here is of minimal importance \n previous_dp_array[-1] = 1 \n # for the ith segment to consider of the k segments needed \n for segment_i in range(k) : \n # we should count the number of valid start partitions based on the previous dp array... but from where do we count? \n valid_start_partitions = 0 \n # we know this segment must start at the 1 indexed sgement position * the minLength, minus 1 since the string is in 0 indexing \n segment_start = ((segment_i + 1) * minLength) - 1 \n # we know this segment must stop at the length of the string less the number of segments less the 1 indexed segment index * minLength \n # this leaves room for the necessary other segments as segment_i will start with k - 1 multiplied by segment length for the remaining sizing \n # over time this will grow until we stop at sL. This keeps our stopping point in range \n segment_stop = sL - (k - (segment_i + 1)) * minLength \n # for the segment index in regards to the string from segment start to segment stop \n for segment_index in range(segment_start, segment_stop) : \n # our dynamic programming array index is necessarily the string index less the minLength (look backwards to the start of the segment prior) \n dp_index = segment_index - minLength\n # if we have a prime value at the 0 indexed dp index -> we know that the string at segment index going back min length is a prime value \n if is_prime_value[dp_index + 1] : \n # this means that the number of valid start partitions here should have been recorded in the previous array at this index \n # we now need to include all of the valid partitions from that point into the next iteration at some time in the current dp array \n valid_start_partitions += previous_dp_array[dp_index]\n # the point at which we need to record it in the future is the point at which this segment index is necessarily not a prime, aka a factor \n # when this segment index, showcasing the end of the segment of minimum size, is a factor, we need to set the current dp array at this point\n # i.e. where the segment could end at, equal to the modular amount of the valid start partitions \n if is_prime_value[segment_index] == False : \n current_dp_array[segment_index] = valid_start_partitions % mod\n # at the end of the current segment_i under consideration, we need to move the previously recorded values into the current \n # and we need to move the current recorded values into the previous. This stores these for the next iteration, until all segments are considered\n current_dp_array, previous_dp_array = previous_dp_array, current_dp_array\n # when done, our previous dp array at the end stores the correct value when modularized \n return previous_dp_array[-1] % mod \n\n```

You are given a string `s` that consists of the digits `'1'` to `'9'` and two integers `k` and `minLength`. A partition of `s` is called **beautiful** if: * `s` is partitioned into `k` non-intersecting substrings. * Each substring has a length of **at least** `minLength`. * Each substring starts with a **prime** digit and ends with a **non-prime** digit. Prime digits are `'2'`, `'3'`, `'5'`, and `'7'`, and the rest of the digits are non-prime. Return _the number of **beautiful** partitions of_ `s`. Since the answer may be very large, return it **modulo** `109 + 7`. A **substring** is a contiguous sequence of characters within a string. **Example 1:** **Input:** s = "23542185131 ", k = 3, minLength = 2 **Output:** 3 **Explanation:** There exists three ways to create a beautiful partition: "2354 | 218 | 5131 " "2354 | 21851 | 31 " "2354218 | 51 | 31 " **Example 2:** **Input:** s = "23542185131 ", k = 3, minLength = 3 **Output:** 1 **Explanation:** There exists one way to create a beautiful partition: "2354 | 218 | 5131 ". **Example 3:** **Input:** s = "3312958 ", k = 3, minLength = 1 **Output:** 1 **Explanation:** There exists one way to create a beautiful partition: "331 | 29 | 58 ". **Constraints:** * `1 <= k, minLength <= s.length <= 1000` * `s` consists of the digits `'1'` to `'9'`.

Efficient Python Solution

minimum-cuts-to-divide-a-circle

# Approach\nThe code efficiently handles the special case where n is equal to 1 and provides a concise solution for determining the number of cuts needed based on whether n is even or odd. Both time and space complexities are constant, making the algorithm efficient for any input size.\n\n# Code\n```\nclass Solution:\n def numberOfCuts(self, n: int) -> int:\n if n == 1:\n return 0\n return n // 2 if n % 2 == 0 else n\n\n\n```

A **valid cut** in a circle can be: * A cut that is represented by a straight line that touches two points on the edge of the circle and passes through its center, or * A cut that is represented by a straight line that touches one point on the edge of the circle and its center. Some valid and invalid cuts are shown in the figures below. Given the integer `n`, return _the **minimum** number of cuts needed to divide a circle into_ `n` _equal slices_. **Example 1:** **Input:** n = 4 **Output:** 2 **Explanation:** The above figure shows how cutting the circle twice through the middle divides it into 4 equal slices. **Example 2:** **Input:** n = 3 **Output:** 3 **Explanation:** At least 3 cuts are needed to divide the circle into 3 equal slices. It can be shown that less than 3 cuts cannot result in 3 slices of equal size and shape. Also note that the first cut will not divide the circle into distinct parts. **Constraints:** * `1 <= n <= 100`

Simple Python Solution

minimum-cuts-to-divide-a-circle

```\nclass Solution(object):\n def numberOfCuts(self, n):\n if n == 1: return 0\n return n // 2 if n % 2 == 0 else n\n```\n**UpVote** Coders! Which motivates me **:)**

A **valid cut** in a circle can be: * A cut that is represented by a straight line that touches two points on the edge of the circle and passes through its center, or * A cut that is represented by a straight line that touches one point on the edge of the circle and its center. Some valid and invalid cuts are shown in the figures below. Given the integer `n`, return _the **minimum** number of cuts needed to divide a circle into_ `n` _equal slices_. **Example 1:** **Input:** n = 4 **Output:** 2 **Explanation:** The above figure shows how cutting the circle twice through the middle divides it into 4 equal slices. **Example 2:** **Input:** n = 3 **Output:** 3 **Explanation:** At least 3 cuts are needed to divide the circle into 3 equal slices. It can be shown that less than 3 cuts cannot result in 3 slices of equal size and shape. Also note that the first cut will not divide the circle into distinct parts. **Constraints:** * `1 <= n <= 100`

Easy Python Solution

minimum-cuts-to-divide-a-circle

# Code\n```\nclass Solution:\n def numberOfCuts(self, n: int) -> int:\n if n==1: return 0\n return n//2 if n%2==0 else n\n```

A **valid cut** in a circle can be: * A cut that is represented by a straight line that touches two points on the edge of the circle and passes through its center, or * A cut that is represented by a straight line that touches one point on the edge of the circle and its center. Some valid and invalid cuts are shown in the figures below. Given the integer `n`, return _the **minimum** number of cuts needed to divide a circle into_ `n` _equal slices_. **Example 1:** **Input:** n = 4 **Output:** 2 **Explanation:** The above figure shows how cutting the circle twice through the middle divides it into 4 equal slices. **Example 2:** **Input:** n = 3 **Output:** 3 **Explanation:** At least 3 cuts are needed to divide the circle into 3 equal slices. It can be shown that less than 3 cuts cannot result in 3 slices of equal size and shape. Also note that the first cut will not divide the circle into distinct parts. **Constraints:** * `1 <= n <= 100`

[C++|Java|Python3] parity

minimum-cuts-to-divide-a-circle

Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/679b6a406693e67fb9637bbd1c8449f2372e76c5) for solutions of biweekly 92. \n\n**Intuition**\nThis is a test of parity. If it is required to have odd number of equal cuts, one has to cut it n time; otherwise, one has to cut n//2 times. \nAn edge case is when n == 1 no cut is required. \n\n**Implementation**\n**C++**\n```\nclass Solution {\npublic:\n int numberOfCuts(int n) {\n if (n == 1) return 0; \n return n&1 ? n : n >> 1; \n }\n};\n```\n\n**Java**\n```\nclass Solution {\n public int numberOfCuts(int n) {\n if (n == 1) return 0; \n return n%2 == 1 ? n : n/2; \n }\n}\n```\n\n**Python3**\n```\nclass Solution:\n def numberOfCuts(self, n: int) -> int:\n if n == 1: return 0 \n return n if n&1 else n//2\n```\n**Complexity**\nTime O(1)\nSpace O(1)

A **valid cut** in a circle can be: * A cut that is represented by a straight line that touches two points on the edge of the circle and passes through its center, or * A cut that is represented by a straight line that touches one point on the edge of the circle and its center. Some valid and invalid cuts are shown in the figures below. Given the integer `n`, return _the **minimum** number of cuts needed to divide a circle into_ `n` _equal slices_. **Example 1:** **Input:** n = 4 **Output:** 2 **Explanation:** The above figure shows how cutting the circle twice through the middle divides it into 4 equal slices. **Example 2:** **Input:** n = 3 **Output:** 3 **Explanation:** At least 3 cuts are needed to divide the circle into 3 equal slices. It can be shown that less than 3 cuts cannot result in 3 slices of equal size and shape. Also note that the first cut will not divide the circle into distinct parts. **Constraints:** * `1 <= n <= 100`

Python || 1 Line Solution || 100% Faster || Explained

minimum-cuts-to-divide-a-circle

1)if n=1 we do not need to cut the circle so, answer will be 0.\n2)if n is even then no. of valid cuts will be equal to n/2.\n3)if n is odd then no. of vaild cuts will be equal to n.\n```\nclass Solution:\n def numberOfCuts(self, n: int) -> int:\n return n if n%2 and n!=1 else n//2\n```\n\n**An upvote will be encouraging**

A **valid cut** in a circle can be: * A cut that is represented by a straight line that touches two points on the edge of the circle and passes through its center, or * A cut that is represented by a straight line that touches one point on the edge of the circle and its center. Some valid and invalid cuts are shown in the figures below. Given the integer `n`, return _the **minimum** number of cuts needed to divide a circle into_ `n` _equal slices_. **Example 1:** **Input:** n = 4 **Output:** 2 **Explanation:** The above figure shows how cutting the circle twice through the middle divides it into 4 equal slices. **Example 2:** **Input:** n = 3 **Output:** 3 **Explanation:** At least 3 cuts are needed to divide the circle into 3 equal slices. It can be shown that less than 3 cuts cannot result in 3 slices of equal size and shape. Also note that the first cut will not divide the circle into distinct parts. **Constraints:** * `1 <= n <= 100`

Shortest solution in C++ and Python. Check it out!

minimum-cuts-to-divide-a-circle

\n\n# C++\n```cpp\nclass Solution {\npublic:\n int numberOfCuts(int n) {\n if(n == 1) return 0;\n return n & 1 ? n : n/2;\n }\n};\n```\n\n# Python\n```py\nclass Solution:\n def numberOfCuts(self, n: int) -> int:\n if(n == 1): return 0\n return n if n & 1 else n//2\n```

A **valid cut** in a circle can be: * A cut that is represented by a straight line that touches two points on the edge of the circle and passes through its center, or * A cut that is represented by a straight line that touches one point on the edge of the circle and its center. Some valid and invalid cuts are shown in the figures below. Given the integer `n`, return _the **minimum** number of cuts needed to divide a circle into_ `n` _equal slices_. **Example 1:** **Input:** n = 4 **Output:** 2 **Explanation:** The above figure shows how cutting the circle twice through the middle divides it into 4 equal slices. **Example 2:** **Input:** n = 3 **Output:** 3 **Explanation:** At least 3 cuts are needed to divide the circle into 3 equal slices. It can be shown that less than 3 cuts cannot result in 3 slices of equal size and shape. Also note that the first cut will not divide the circle into distinct parts. **Constraints:** * `1 <= n <= 100`

Python one-liner

minimum-cuts-to-divide-a-circle

# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe need to divide n by 2 if n==1 or n is even.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numberOfCuts(self, n: int) -> int:\n return n >> (not n&1 or n==1)\n```

A **valid cut** in a circle can be: * A cut that is represented by a straight line that touches two points on the edge of the circle and passes through its center, or * A cut that is represented by a straight line that touches one point on the edge of the circle and its center. Some valid and invalid cuts are shown in the figures below. Given the integer `n`, return _the **minimum** number of cuts needed to divide a circle into_ `n` _equal slices_. **Example 1:** **Input:** n = 4 **Output:** 2 **Explanation:** The above figure shows how cutting the circle twice through the middle divides it into 4 equal slices. **Example 2:** **Input:** n = 3 **Output:** 3 **Explanation:** At least 3 cuts are needed to divide the circle into 3 equal slices. It can be shown that less than 3 cuts cannot result in 3 slices of equal size and shape. Also note that the first cut will not divide the circle into distinct parts. **Constraints:** * `1 <= n <= 100`

Python || C++ || o(1) || beats 100%

minimum-cuts-to-divide-a-circle

# Complexity\n- Time complexity: $$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# C++\n```\nclass Solution {\npublic:\n int numberOfCuts(int n) {\n return (n%2 == 0 ? n/2 : n!=1 ? n : 0) ;\n \n }\n};\n```\n\n\n# Python\n```\nclass Solution:\n def numberOfCuts(self, n: int) -> int:\n\n if n== 1 : return 0\n\n return n if n%2 else n//2\n```

A **valid cut** in a circle can be: * A cut that is represented by a straight line that touches two points on the edge of the circle and passes through its center, or * A cut that is represented by a straight line that touches one point on the edge of the circle and its center. Some valid and invalid cuts are shown in the figures below. Given the integer `n`, return _the **minimum** number of cuts needed to divide a circle into_ `n` _equal slices_. **Example 1:** **Input:** n = 4 **Output:** 2 **Explanation:** The above figure shows how cutting the circle twice through the middle divides it into 4 equal slices. **Example 2:** **Input:** n = 3 **Output:** 3 **Explanation:** At least 3 cuts are needed to divide the circle into 3 equal slices. It can be shown that less than 3 cuts cannot result in 3 slices of equal size and shape. Also note that the first cut will not divide the circle into distinct parts. **Constraints:** * `1 <= n <= 100`

【Video】Give me 5 minutes - How we think about a solution

difference-between-ones-and-zeros-in-row-and-column

# Intuition\nCalcuate sum of 1 in each row and column at first.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/swafoNFu99o\n\n\n\u25A0 Timeline of the video\n\n`0:06` Create number of 1 in each row and column\n`1:16` How to calculate numbers at each position \n`4:03` Coding\n`6:32` Time Complexity and Space Complexity\n`7:02` Explain zip(*grid)\n`8:15` Step by step algorithm of my solution code\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 3,451\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n---\n\n# Approach\n\n## How we think about a solution\n\nSimply, If we calculate sum of each row and column, we can solve this question.\n\nThis is my first solution code.\n\n```\nclass Solution:\n def onesMinusZeros(self, grid: List[List[int]]) -> List[List[int]]:\n m = len(grid)\n n = len(grid[0])\n\n rows = {}\n for r in range(m): \n row_sum = 0\n for c in range(n):\n row_sum += grid[r][c]\n \n rows[r] = row_sum\n\n cols = {}\n for c in range(n):\n col_sum = 0\n for r in range(m):\n col_sum += grid[r][c]\n \n cols[c] = col_sum\n\n res = [[0] * n for _ in range(m)]\n\n for r in range(m):\n for c in range(n):\n res[r][c] = rows[r] + cols[c] - (m - rows[r]) - (n - cols[c])\n \n return res\n```\n\nummm....it\'s long \uD83D\uDE05. I wanted to make it a bit cooler. Anyway, you can see my second solution code below. Let me explain one by one.\n\n```\nInput: grid = [[0,1,1],[1,0,1],[0,0,1]]\n```\n\nSimply, I thought that knowing the sum of each row and column would be sufficient to solve it.\n\n```\n[0,1,1] \u2192 2\n[1,0,1] \u2192 2\n[0,0,1] \u2192 1\n \u2193 \u2193 \u2193\n 1 1 3 \n```\n\n```\nones_row = [2,2,1] \nones_col = [1,1,3] \n```\nAll we have to do is just to calculate them for each positions in diff matrix.\n\n`ones_row` and `ones_col` have number of `1` in each row or each column, so number of `0` should be\n\n```\nFor each row : length of row - number of 1 in each row\nFor each column : length of column - number of 1 in each column\n```\nIn Python solution code below\n```\nones_row[i] + ones_col[j] - (m - ones_row[i]) - (n - ones_col[j])\n\nones_row[i]: number of 1 in the row\nones_col[i]: number of 1 in the column\n(m - ones_row[i]): number of 0 in the row\n(n - ones_col[j]): number of 0 in the column\n\nm is length of row\nn is length of column\n```\n\nEasy! \uD83D\uDE04\nLet\'s see a real algorithm!\n\n\n---\n\n\n# Complexity\n- Time complexity: $$O(m * n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(m * n)$$ or $$O(m + n)$$\nIf we can ignore `res`, space should be $$O(m + n)$$ for `ones_row` and `ones_col`.\n\n# Solution code\n\n```python []\nclass Solution:\n def onesMinusZeros(self, grid: List[List[int]]) -> List[List[int]]:\n m = len(grid)\n n = len(grid[0])\n res = [[0] * n for _ in range(m)]\n ones_row = [row.count(1) for row in grid]\n ones_col = [col.count(1) for col in zip(*grid)]\n\n for i in range(m):\n for j in range(n):\n res[i][j] = ones_row[i] + ones_col[j] - (m - ones_row[i]) - (n - ones_col[j])\n\n return res\n```\n```javascript []\nvar onesMinusZeros = function(grid) {\n const m = grid.length;\n const n = grid[0].length;\n const res = Array.from({ length: m }, () => Array(n).fill(0));\n const onesRow = grid.map(row => row.filter(val => val === 1).length);\n const onesCol = Array.from({ length: n }, (_, j) => grid.map(row => row[j]).filter(val => val === 1).length);\n\n for (let i = 0; i < m; i++) {\n for (let j = 0; j < n; j++) {\n res[i][j] = onesRow[i] + onesCol[j] - (m - onesRow[i]) - (n - onesCol[j]);\n }\n }\n\n return res; \n};\n```\n```java []\nclass Solution {\n public int[][] onesMinusZeros(int[][] grid) {\n int m = grid.length;\n int n = grid[0].length;\n int[][] res = new int[m][n];\n int[] onesRow = new int[m];\n int[] onesCol = new int[n];\n\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n onesRow[i] += grid[i][j];\n onesCol[j] += grid[i][j];\n }\n }\n\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n res[i][j] = onesRow[i] + onesCol[j] - (m - onesRow[i]) - (n - onesCol[j]);\n }\n }\n\n return res; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> onesMinusZeros(vector<vector<int>>& grid) {\n int m = grid.size();\n int n = grid[0].size();\n vector<vector<int>> res(m, vector<int>(n, 0));\n vector<int> onesRow(m, 0);\n vector<int> onesCol(n, 0);\n\n for (int i = 0; i < m; i++) {\n onesRow[i] = count(grid[i].begin(), grid[i].end(), 1);\n }\n\n for (int j = 0; j < n; j++) {\n for (int i = 0; i < m; i++) {\n onesCol[j] += grid[i][j];\n }\n }\n\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n res[i][j] = onesRow[i] + onesCol[j] - (m - onesRow[i]) - (n - onesCol[j]);\n }\n }\n\n return res; \n }\n};\n```\n\n## Pyhon Tips\n\nLet me explain about\n```\nzip(*grid)\n```\nFirst of all, `*grid` creates\n```\ngrid = [[1,2,3],[4,5,6],[7,8,9]]\n\u2193\n[1,2,3] [4,5,6] [7,8,9]\n```\nThen zip function deals with numbers at the same index of each element. That means we can deal with the numbers at the same column index.\n\n```\n[1,2,3] [4,5,6] [7,8,9]\n\u2193\n(1, 4, 7),(2, 5, 8),(3, 6, 9)\n\n(1, 4, 7): column index 0\n(2, 5, 8): column index 1\n(3, 6, 9): column index 2\n\n[1,2,3]\n[4,5,6]\n[7,8,9]\n\n```\nThat\'s why we can count number of `1` in each column with\n```\nones_col = [col.count(1) for col in zip(*grid)]\n```\n\n\n\n## Step by step algorithm\n\n1. **Initialize Variables:**\n - Get the number of rows `m` and columns `n` in the `grid`.\n - Create an empty 2D list `res` with dimensions `m x n` initialized to zeros.\n\n ```python\n m = len(grid)\n n = len(grid[0])\n res = [[0] * n for _ in range(m)]\n ```\n\n2. **Calculate Ones in Each Row and Column:**\n - Calculate the number of ones in each row and store the results in the list `ones_row`.\n - Calculate the number of ones in each column using `zip(*grid)` and store the results in the list `ones_col`.\n\n ```python\n ones_row = [row.count(1) for row in grid]\n ones_col = [col.count(1) for col in zip(*grid)]\n ```\n\n3. **Fill the Result Matrix:**\n - Use nested loops to iterate through each element of the result matrix.\n - For each element at position `(i, j)`, calculate its value using the formula:\n ```\n res[i][j] = ones_row[i] + ones_col[j] - (m - ones_row[i]) - (n - ones_col[j])\n ```\n\n ```python\n for i in range(m):\n for j in range(n):\n res[i][j] = ones_row[i] + ones_col[j] - (m - ones_row[i]) - (n - ones_col[j])\n ```\n\n4. **Return the Result:**\n - Return the computed result matrix.\n\n ```python\n return res\n ```\n\nIn summary, the algorithm calculates the number of ones in each row and column of the input matrix and uses this information to compute the values for each element in the result matrix using a specified formula.\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/destination-city/solutions/4406091/video-give-me-3-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/tjILACCjQI0\n\n\u25A0 Timeline of the video\n\n`0:04` Explain how we can solve this question\n`1:29` Coding\n`2:40` Time Complexity and Space Complexity\n`3:13` Step by step algorithm of my solution code\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/special-positions-in-a-binary-matrix/solutions/4397604/video-give-me-5-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/qTAh4HGfUHk\n\n\u25A0 Timeline of the video\n\n`0:05` Explain algorithm of the first step\n`1:06` Explain algorithm of the second step\n`2:36` Coding\n`4:17` Time Complexity and Space Complexity\n`4:55` Step by step algorithm of my solution code\n

You are given a **0-indexed** `m x n` binary matrix `grid`. A **0-indexed** `m x n` difference matrix `diff` is created with the following procedure: * Let the number of ones in the `ith` row be `onesRowi`. * Let the number of ones in the `jth` column be `onesColj`. * Let the number of zeros in the `ith` row be `zerosRowi`. * Let the number of zeros in the `jth` column be `zerosColj`. * `diff[i][j] = onesRowi + onesColj - zerosRowi - zerosColj` Return _the difference matrix_ `diff`. **Example 1:** **Input:** grid = \[\[0,1,1\],\[1,0,1\],\[0,0,1\]\] **Output:** \[\[0,0,4\],\[0,0,4\],\[-2,-2,2\]\] **Explanation:** - diff\[0\]\[0\] = `onesRow0 + onesCol0 - zerosRow0 - zerosCol0` = 2 + 1 - 1 - 2 = 0 - diff\[0\]\[1\] = `onesRow0 + onesCol1 - zerosRow0 - zerosCol1` = 2 + 1 - 1 - 2 = 0 - diff\[0\]\[2\] = `onesRow0 + onesCol2 - zerosRow0 - zerosCol2` = 2 + 3 - 1 - 0 = 4 - diff\[1\]\[0\] = `onesRow1 + onesCol0 - zerosRow1 - zerosCol0` = 2 + 1 - 1 - 2 = 0 - diff\[1\]\[1\] = `onesRow1 + onesCol1 - zerosRow1 - zerosCol1` = 2 + 1 - 1 - 2 = 0 - diff\[1\]\[2\] = `onesRow1 + onesCol2 - zerosRow1 - zerosCol2` = 2 + 3 - 1 - 0 = 4 - diff\[2\]\[0\] = `onesRow2 + onesCol0 - zerosRow2 - zerosCol0` = 1 + 1 - 2 - 2 = -2 - diff\[2\]\[1\] = `onesRow2 + onesCol1 - zerosRow2 - zerosCol1` = 1 + 1 - 2 - 2 = -2 - diff\[2\]\[2\] = `onesRow2 + onesCol2 - zerosRow2 - zerosCol2` = 1 + 3 - 2 - 0 = 2 **Example 2:** **Input:** grid = \[\[1,1,1\],\[1,1,1\]\] **Output:** \[\[5,5,5\],\[5,5,5\]\] **Explanation:** - diff\[0\]\[0\] = onesRow0 + onesCol0 - zerosRow0 - zerosCol0 = 3 + 2 - 0 - 0 = 5 - diff\[0\]\[1\] = onesRow0 + onesCol1 - zerosRow0 - zerosCol1 = 3 + 2 - 0 - 0 = 5 - diff\[0\]\[2\] = onesRow0 + onesCol2 - zerosRow0 - zerosCol2 = 3 + 2 - 0 - 0 = 5 - diff\[1\]\[0\] = onesRow1 + onesCol0 - zerosRow1 - zerosCol0 = 3 + 2 - 0 - 0 = 5 - diff\[1\]\[1\] = onesRow1 + onesCol1 - zerosRow1 - zerosCol1 = 3 + 2 - 0 - 0 = 5 - diff\[1\]\[2\] = onesRow1 + onesCol2 - zerosRow1 - zerosCol2 = 3 + 2 - 0 - 0 = 5 **Constraints:** * `m == grid.length` * `n == grid[i].length` * `1 <= m, n <= 105` * `1 <= m * n <= 105` * `grid[i][j]` is either `0` or `1`.

💯Faster✅💯🔥🔥EASY SOLUTION FOR BEGINNER FRIENDLY🔥🔥

difference-between-ones-and-zeros-in-row-and-column

# Approach\n\n1. Iterate through each element in the input grid.\n2. Calculate the sum of ones and zeros in each row and column.\n3. Create a new jagged array and populate it with the differences between the counts of ones and zeros in each corresponding row and column.\n\n# Complexity\n\n- **Time complexity:** O(n * m), where n is the number of rows and m is the number of columns in the grid. The double loop iterates through all elements of the grid.\n- **Space complexity:** O(n + m), for the row and col arrays.\n\n# Code\n```csharp []\npublic class Solution {\n public int[][] OnesMinusZeros(int[][] grid)\n {\n int n = grid.Length;\n int m = grid[0].Length;\n int[] col = new int[m];\n int[] row = new int[n];\n for (int i = 0;i < n; i++)\n {\n for (int j = 0; j < m; j++)\n {\n row[i] += (grid[i][j] == 1) ? 1 : -1;\n col[j] += (grid[i][j] == 1) ? 1 : -1;\n }\n }\n int[][] jaggedArray = new int[n][];\n\n for (int i = 0; i < n; i++)\n {\n jaggedArray[i] = new int[m];\n for (int j = 0; j < m; j++)\n {\n jaggedArray[i][j] = col[j] + row[i];\n }\n }\n return jaggedArray;\n }\n}\n```\n```java []\npublic class Solution {\n public int[][] onesMinusZeros(int[][] grid) {\n int n = grid.length;\n int m = grid[0].length;\n int[] col = new int[m];\n int[] row = new int[n];\n\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < m; j++) {\n row[i] += (grid[i][j] == 1) ? 1 : -1;\n col[j] += (grid[i][j] == 1) ? 1 : -1;\n }\n }\n\n int[][] jaggedArray = new int[n][];\n\n for (int i = 0; i < n; i++) {\n jaggedArray[i] = new int[m];\n for (int j = 0; j < m; j++) {\n jaggedArray[i][j] = col[j] + row[i];\n }\n }\n\n return jaggedArray;\n }\n}\n```\n```go []\nfunc onesMinusZeros(grid [][]int) [][]int {\n\tn := len(grid)\n\tm := len(grid[0])\n\tcol := make([]int, m)\n\trow := make([]int, n)\n\n\tfor i := 0; i < n; i++ {\n\t\tfor j := 0; j < m; j++ {\n\t\t\tif grid[i][j] == 1 {\n\t\t\t\trow[i]++\n\t\t\t\tcol[j]++\n\t\t\t} else {\n\t\t\t\trow[i]--\n\t\t\t\tcol[j]--\n\t\t\t}\n\t\t}\n\t}\n\n\tjaggedArray := make([][]int, n)\n\n\tfor i := 0; i < n; i++ {\n\t\tjaggedArray[i] = make([]int, m)\n\t\tfor j := 0; j < m; j++ {\n\t\t\tjaggedArray[i][j] = col[j] + row[i]\n\t\t}\n\t}\n\n\treturn jaggedArray\n}\n```\n```python []\nclass Solution:\n def ones_minus_zeros(self, grid):\n n = len(grid)\n m = len(grid[0])\n col = [0] * m\n row = [0] * n\n\n for i in range(n):\n for j in range(m):\n row[i] += 1 if grid[i][j] == 1 else -1\n col[j] += 1 if grid[i][j] == 1 else -1\n\n jagged_array = [[col[j] + row[i] for j in range(m)] for i in range(n)]\n\n return jagged_array\n```\n\n\n- Please upvote me !!!

You are given a **0-indexed** `m x n` binary matrix `grid`. A **0-indexed** `m x n` difference matrix `diff` is created with the following procedure: * Let the number of ones in the `ith` row be `onesRowi`. * Let the number of ones in the `jth` column be `onesColj`. * Let the number of zeros in the `ith` row be `zerosRowi`. * Let the number of zeros in the `jth` column be `zerosColj`. * `diff[i][j] = onesRowi + onesColj - zerosRowi - zerosColj` Return _the difference matrix_ `diff`. **Example 1:** **Input:** grid = \[\[0,1,1\],\[1,0,1\],\[0,0,1\]\] **Output:** \[\[0,0,4\],\[0,0,4\],\[-2,-2,2\]\] **Explanation:** - diff\[0\]\[0\] = `onesRow0 + onesCol0 - zerosRow0 - zerosCol0` = 2 + 1 - 1 - 2 = 0 - diff\[0\]\[1\] = `onesRow0 + onesCol1 - zerosRow0 - zerosCol1` = 2 + 1 - 1 - 2 = 0 - diff\[0\]\[2\] = `onesRow0 + onesCol2 - zerosRow0 - zerosCol2` = 2 + 3 - 1 - 0 = 4 - diff\[1\]\[0\] = `onesRow1 + onesCol0 - zerosRow1 - zerosCol0` = 2 + 1 - 1 - 2 = 0 - diff\[1\]\[1\] = `onesRow1 + onesCol1 - zerosRow1 - zerosCol1` = 2 + 1 - 1 - 2 = 0 - diff\[1\]\[2\] = `onesRow1 + onesCol2 - zerosRow1 - zerosCol2` = 2 + 3 - 1 - 0 = 4 - diff\[2\]\[0\] = `onesRow2 + onesCol0 - zerosRow2 - zerosCol0` = 1 + 1 - 2 - 2 = -2 - diff\[2\]\[1\] = `onesRow2 + onesCol1 - zerosRow2 - zerosCol1` = 1 + 1 - 2 - 2 = -2 - diff\[2\]\[2\] = `onesRow2 + onesCol2 - zerosRow2 - zerosCol2` = 1 + 3 - 2 - 0 = 2 **Example 2:** **Input:** grid = \[\[1,1,1\],\[1,1,1\]\] **Output:** \[\[5,5,5\],\[5,5,5\]\] **Explanation:** - diff\[0\]\[0\] = onesRow0 + onesCol0 - zerosRow0 - zerosCol0 = 3 + 2 - 0 - 0 = 5 - diff\[0\]\[1\] = onesRow0 + onesCol1 - zerosRow0 - zerosCol1 = 3 + 2 - 0 - 0 = 5 - diff\[0\]\[2\] = onesRow0 + onesCol2 - zerosRow0 - zerosCol2 = 3 + 2 - 0 - 0 = 5 - diff\[1\]\[0\] = onesRow1 + onesCol0 - zerosRow1 - zerosCol0 = 3 + 2 - 0 - 0 = 5 - diff\[1\]\[1\] = onesRow1 + onesCol1 - zerosRow1 - zerosCol1 = 3 + 2 - 0 - 0 = 5 - diff\[1\]\[2\] = onesRow1 + onesCol2 - zerosRow1 - zerosCol2 = 3 + 2 - 0 - 0 = 5 **Constraints:** * `m == grid.length` * `n == grid[i].length` * `1 <= m, n <= 105` * `1 <= m * n <= 105` * `grid[i][j]` is either `0` or `1`.

Lets learn Python 🐍🐍

difference-between-ones-and-zeros-in-row-and-column

\n`diff[i][j] = onesRowi + onesColj - zerosRowi - zerosColj`\n\n# Complexity\n- Time complexity: O (MN)\n\n\n``` Python []\nclass Solution:\n def onesMinusZeros(self, grid: List[List[int]]) -> List[List[int]]:\n def summation(nums) : \n return 2 * sum(nums) - len(nums)\n m, n = len(grid), len(grid[0])\n \n rows = list(map(summation, grid))\n cols = list(map(summation, zip(*grid)))\n \n for i,j in product(range(m), range(n)):\n grid[i][j] = rows[i] + cols[j]\n return grid\n```\n\n# Explanation\n- `summation` function : Returns : `onesRowi - zerosRowi`\n```\nres = onesRowi - zerosRowi\nres = onesRowi - ( length - onesRowi )\nres = 2 * onesRowi - length\nonesRowi -> sumRowi\n```\n- `diff[i][j]` = `res_row + res_col`\n- `zip())` : Create an iterator that produces tuples picking up elements from same indexes of given arguments\n- `*grid` : Gives the rows of matrix\n- `zip(*grid)` : Return Transpose of matrix\n- `product(range(m), range(n))` : Cartesian Product of iterators\n

You are given a **0-indexed** `m x n` binary matrix `grid`. A **0-indexed** `m x n` difference matrix `diff` is created with the following procedure: * Let the number of ones in the `ith` row be `onesRowi`. * Let the number of ones in the `jth` column be `onesColj`. * Let the number of zeros in the `ith` row be `zerosRowi`. * Let the number of zeros in the `jth` column be `zerosColj`. * `diff[i][j] = onesRowi + onesColj - zerosRowi - zerosColj` Return _the difference matrix_ `diff`. **Example 1:** **Input:** grid = \[\[0,1,1\],\[1,0,1\],\[0,0,1\]\] **Output:** \[\[0,0,4\],\[0,0,4\],\[-2,-2,2\]\] **Explanation:** - diff\[0\]\[0\] = `onesRow0 + onesCol0 - zerosRow0 - zerosCol0` = 2 + 1 - 1 - 2 = 0 - diff\[0\]\[1\] = `onesRow0 + onesCol1 - zerosRow0 - zerosCol1` = 2 + 1 - 1 - 2 = 0 - diff\[0\]\[2\] = `onesRow0 + onesCol2 - zerosRow0 - zerosCol2` = 2 + 3 - 1 - 0 = 4 - diff\[1\]\[0\] = `onesRow1 + onesCol0 - zerosRow1 - zerosCol0` = 2 + 1 - 1 - 2 = 0 - diff\[1\]\[1\] = `onesRow1 + onesCol1 - zerosRow1 - zerosCol1` = 2 + 1 - 1 - 2 = 0 - diff\[1\]\[2\] = `onesRow1 + onesCol2 - zerosRow1 - zerosCol2` = 2 + 3 - 1 - 0 = 4 - diff\[2\]\[0\] = `onesRow2 + onesCol0 - zerosRow2 - zerosCol0` = 1 + 1 - 2 - 2 = -2 - diff\[2\]\[1\] = `onesRow2 + onesCol1 - zerosRow2 - zerosCol1` = 1 + 1 - 2 - 2 = -2 - diff\[2\]\[2\] = `onesRow2 + onesCol2 - zerosRow2 - zerosCol2` = 1 + 3 - 2 - 0 = 2 **Example 2:** **Input:** grid = \[\[1,1,1\],\[1,1,1\]\] **Output:** \[\[5,5,5\],\[5,5,5\]\] **Explanation:** - diff\[0\]\[0\] = onesRow0 + onesCol0 - zerosRow0 - zerosCol0 = 3 + 2 - 0 - 0 = 5 - diff\[0\]\[1\] = onesRow0 + onesCol1 - zerosRow0 - zerosCol1 = 3 + 2 - 0 - 0 = 5 - diff\[0\]\[2\] = onesRow0 + onesCol2 - zerosRow0 - zerosCol2 = 3 + 2 - 0 - 0 = 5 - diff\[1\]\[0\] = onesRow1 + onesCol0 - zerosRow1 - zerosCol0 = 3 + 2 - 0 - 0 = 5 - diff\[1\]\[1\] = onesRow1 + onesCol1 - zerosRow1 - zerosCol1 = 3 + 2 - 0 - 0 = 5 - diff\[1\]\[2\] = onesRow1 + onesCol2 - zerosRow1 - zerosCol2 = 3 + 2 - 0 - 0 = 5 **Constraints:** * `m == grid.length` * `n == grid[i].length` * `1 <= m, n <= 105` * `1 <= m * n <= 105` * `grid[i][j]` is either `0` or `1`.

Easy data preprocessing optimized solution!

difference-between-ones-and-zeros-in-row-and-column

# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n* To keep track of how many 1s are in each row and column, use arrays: one array for each row and another array for each column. \n* Now, we can quickly determine how many 0s there are in each row or column once you know how many 1s there are in each one by using \nm - onesRow[i] for number of zeros in ith row\nn - onesCols[j] for number of zeros in jth col\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def onesMinusZeros(self, grid: List[List[int]]) -> List[List[int]]:\n m , n = len(grid) , len(grid[0 ])\n onesRow , onesCol = [0] * m , [0] * n \n for i in range(m):\n for j in range(n):\n if grid[i][j] == 1:\n onesRow[i] += 1\n onesCol[j] += 1 \n for i in range(m):\n for j in range(n):\n grid[i][j] = onesRow[i] + onesCol[j] -(m - onesRow[i] + n - onesCol[j])\n return grid\n \n```

You are given a **0-indexed** `m x n` binary matrix `grid`. A **0-indexed** `m x n` difference matrix `diff` is created with the following procedure: * Let the number of ones in the `ith` row be `onesRowi`. * Let the number of ones in the `jth` column be `onesColj`. * Let the number of zeros in the `ith` row be `zerosRowi`. * Let the number of zeros in the `jth` column be `zerosColj`. * `diff[i][j] = onesRowi + onesColj - zerosRowi - zerosColj` Return _the difference matrix_ `diff`. **Example 1:** **Input:** grid = \[\[0,1,1\],\[1,0,1\],\[0,0,1\]\] **Output:** \[\[0,0,4\],\[0,0,4\],\[-2,-2,2\]\] **Explanation:** - diff\[0\]\[0\] = `onesRow0 + onesCol0 - zerosRow0 - zerosCol0` = 2 + 1 - 1 - 2 = 0 - diff\[0\]\[1\] = `onesRow0 + onesCol1 - zerosRow0 - zerosCol1` = 2 + 1 - 1 - 2 = 0 - diff\[0\]\[2\] = `onesRow0 + onesCol2 - zerosRow0 - zerosCol2` = 2 + 3 - 1 - 0 = 4 - diff\[1\]\[0\] = `onesRow1 + onesCol0 - zerosRow1 - zerosCol0` = 2 + 1 - 1 - 2 = 0 - diff\[1\]\[1\] = `onesRow1 + onesCol1 - zerosRow1 - zerosCol1` = 2 + 1 - 1 - 2 = 0 - diff\[1\]\[2\] = `onesRow1 + onesCol2 - zerosRow1 - zerosCol2` = 2 + 3 - 1 - 0 = 4 - diff\[2\]\[0\] = `onesRow2 + onesCol0 - zerosRow2 - zerosCol0` = 1 + 1 - 2 - 2 = -2 - diff\[2\]\[1\] = `onesRow2 + onesCol1 - zerosRow2 - zerosCol1` = 1 + 1 - 2 - 2 = -2 - diff\[2\]\[2\] = `onesRow2 + onesCol2 - zerosRow2 - zerosCol2` = 1 + 3 - 2 - 0 = 2 **Example 2:** **Input:** grid = \[\[1,1,1\],\[1,1,1\]\] **Output:** \[\[5,5,5\],\[5,5,5\]\] **Explanation:** - diff\[0\]\[0\] = onesRow0 + onesCol0 - zerosRow0 - zerosCol0 = 3 + 2 - 0 - 0 = 5 - diff\[0\]\[1\] = onesRow0 + onesCol1 - zerosRow0 - zerosCol1 = 3 + 2 - 0 - 0 = 5 - diff\[0\]\[2\] = onesRow0 + onesCol2 - zerosRow0 - zerosCol2 = 3 + 2 - 0 - 0 = 5 - diff\[1\]\[0\] = onesRow1 + onesCol0 - zerosRow1 - zerosCol0 = 3 + 2 - 0 - 0 = 5 - diff\[1\]\[1\] = onesRow1 + onesCol1 - zerosRow1 - zerosCol1 = 3 + 2 - 0 - 0 = 5 - diff\[1\]\[2\] = onesRow1 + onesCol2 - zerosRow1 - zerosCol2 = 3 + 2 - 0 - 0 = 5 **Constraints:** * `m == grid.length` * `n == grid[i].length` * `1 <= m, n <= 105` * `1 <= m * n <= 105` * `grid[i][j]` is either `0` or `1`.

✅☑[C++/Java/Python/JavaScript] || Easy Approach || EXPLAINED🔥

difference-between-ones-and-zeros-in-row-and-column

# PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n(***For more optimized code use dynamic memory allocation***)\n\n1. **Variable Declarations:**\n\n - `row` and `col`: Store the number of rows and columns in the grid.\n - `diff`: A matrix initialized with the size of `row` rows and co`l columns to store the differences.\n - `r` and `c`: Vectors to store counts of ones in each row and column, respectively.\n1. **Counting Ones in Rows and Columns:**\n\n - Two nested loops iterate through the grid to calculate the count of ones in each row (`r`) and column (`c`) by summing the elements.\n1. **Calculating Differences:**\n\n - Another pair of nested loops calculates the differences (`diff`) between the count of ones and zeros in rows and columns using the provided formula.\n1. **Return:**\n\n - Returns the matrix `diff` containing the calculated differences.\n\n\n\n# Complexity\n- *Time complexity:*\n $$O(row * col)$$\n \n\n- *Space complexity:*\n $$O(row + col)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n // Function to calculate the difference between the count of ones and zeros in the rows and columns of a matrix\n vector<vector<int>> onesMinusZeros(vector<vector<int>>& grid) {\n int row = grid.size(); // Get the number of rows in the grid\n int col = grid[0].size(); // Get the number of columns in the grid\n\n vector<vector<int>> diff(row, vector<int>(col)); // Create a matrix to store differences\n\n vector<int> r(row); // Create a vector to store counts of ones in each row\n vector<int> c(col); // Create a vector to store counts of ones in each column\n\n // Calculate counts of ones in rows and columns\n for(int i = 0; i < row; i++){\n for(int j = 0; j < col; j++){\n r[i] += grid[i][j]; // Sum the elements in each row\n c[j] += grid[i][j]; // Sum the elements in each column\n }\n }\n\n // Calculate the difference between the count of ones and zeros in rows and columns\n for(int i = 0; i < row; i++){\n for(int j = 0; j < col; j++){\n // Calculate the difference using the formula: 2 * (count of ones in row i + count of ones in column j) - (total row count + total column count)\n diff[i][j] = 2 * (r[i] + c[j]) - row - col;\n }\n }\n\n return diff; // Return the matrix containing differences\n }\n};\n\n\n\n```\n```C []\n\n// Function to calculate the difference between the count of ones and zeros in the rows and columns of a matrix\nint** onesMinusZeros(int** grid, int row, int col) {\n int** diff = (int**)malloc(row * sizeof(int*)); // Create a matrix to store differences\n\n int* r = (int*)calloc(row, sizeof(int)); // Create an array to store counts of ones in each row\n int* c = (int*)calloc(col, sizeof(int)); // Create an array to store counts of ones in each column\n\n // Allocate memory for the rows in the difference matrix\n for (int i = 0; i < row; i++) {\n diff[i] = (int*)malloc(col * sizeof(int));\n }\n\n // Calculate counts of ones in rows and columns\n for (int i = 0; i < row; i++) {\n for (int j = 0; j < col; j++) {\n r[i] += grid[i][j]; // Sum the elements in each row\n c[j] += grid[i][j]; // Sum the elements in each column\n }\n }\n\n // Calculate the difference between the count of ones and zeros in rows and columns\n for (int i = 0; i < row; i++) {\n for (int j = 0; j < col; j++) {\n // Calculate the difference using the formula: 2 * (count of ones in row i + count of ones in column j) - (total row count + total column count)\n diff[i][j] = 2 * (r[i] + c[j]) - row - col;\n }\n }\n\n return diff; // Return the matrix containing differences\n}\n\n\n\n```\n```Java []\n\n\nclass Solution {\n public int[][] onesMinusZeros(int[][] grid) {\n int row = grid.length; // Get the number of rows in the grid\n int col = grid[0].length; // Get the number of columns in the grid\n\n int[][] diff = new int[row][col]; // Create a matrix to store differences\n\n int[] r = new int[row]; // Create an array to store counts of ones in each row\n int[] c = new int[col]; // Create an array to store counts of ones in each column\n\n // Calculate counts of ones in rows and columns\n for (int i = 0; i < row; i++) {\n for (int j = 0; j < col; j++) {\n r[i] += grid[i][j]; // Sum the elements in each row\n c[j] += grid[i][j]; // Sum the elements in each column\n }\n }\n\n // Calculate the difference between the count of ones and zeros in rows and columns\n for (int i = 0; i < row; i++) {\n for (int j = 0; j < col; j++) {\n // Calculate the difference using the formula: 2 * (count of ones in row i + count of ones in column j) - (total row count + total column count)\n diff[i][j] = 2 * (r[i] + c[j]) - row - col;\n }\n }\n\n return diff; // Return the matrix containing differences\n }\n}\n\n\n\n```\n```python3 []\nclass Solution:\n def onesMinusZeros(self, grid: List[List[int]]) -> List[List[int]]:\n row = len(grid) # Get the number of rows in the grid\n col = len(grid[0]) # Get the number of columns in the grid\n\n diff = [[0] * col for _ in range(row)] # Create a matrix to store differences\n\n r = [0] * row # Create a list to store counts of ones in each row\n c = [0] * col # Create a list to store counts of ones in each column\n\n # Calculate counts of ones in rows and columns\n for i in range(row):\n for j in range(col):\n r[i] += grid[i][j] # Sum the elements in each row\n c[j] += grid[i][j] # Sum the elements in each column\n\n # Calculate the difference between the count of ones and zeros in rows and columns\n for i in range(row):\n for j in range(col):\n # Calculate the difference using the formula: 2 * (count of ones in row i + count of ones in column j) - (total row count + total column count)\n diff[i][j] = 2 * (r[i] + c[j]) - row - col\n\n return diff # Return the matrix containing differences\n\n\n\n```\n```javascript []\n// Function to calculate the difference between the count of ones and zeros in the rows and columns of a matrix\nfunction onesMinusZeros(grid) {\n const row = grid.length; // Get the number of rows in the grid\n const col = grid[0].length; // Get the number of columns in the grid\n\n const diff = new Array(row).fill().map(() => new Array(col)); // Create a matrix to store differences\n\n const r = new Array(row).fill(0); // Create an array to store counts of ones in each row\n const c = new Array(col).fill(0); // Create an array to store counts of ones in each column\n\n // Calculate counts of ones in rows and columns\n for (let i = 0; i < row; i++) {\n for (let j = 0; j < col; j++) {\n r[i] += grid[i][j]; // Sum the elements in each row\n c[j] += grid[i][j]; // Sum the elements in each column\n }\n }\n\n // Calculate the difference between the count of ones and zeros in rows and columns\n for (let i = 0; i < row; i++) {\n for (let j = 0; j < col; j++) {\n // Calculate the difference using the formula: 2 * (count of ones in row i + count of ones in column j) - (total row count + total column count)\n diff[i][j] = 2 * (r[i] + c[j]) - row - col;\n }\n }\n\n return diff; // Return the matrix containing differences\n}\n\n\n```\n\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n---

You are given a **0-indexed** `m x n` binary matrix `grid`. A **0-indexed** `m x n` difference matrix `diff` is created with the following procedure: * Let the number of ones in the `ith` row be `onesRowi`. * Let the number of ones in the `jth` column be `onesColj`. * Let the number of zeros in the `ith` row be `zerosRowi`. * Let the number of zeros in the `jth` column be `zerosColj`. * `diff[i][j] = onesRowi + onesColj - zerosRowi - zerosColj` Return _the difference matrix_ `diff`. **Example 1:** **Input:** grid = \[\[0,1,1\],\[1,0,1\],\[0,0,1\]\] **Output:** \[\[0,0,4\],\[0,0,4\],\[-2,-2,2\]\] **Explanation:** - diff\[0\]\[0\] = `onesRow0 + onesCol0 - zerosRow0 - zerosCol0` = 2 + 1 - 1 - 2 = 0 - diff\[0\]\[1\] = `onesRow0 + onesCol1 - zerosRow0 - zerosCol1` = 2 + 1 - 1 - 2 = 0 - diff\[0\]\[2\] = `onesRow0 + onesCol2 - zerosRow0 - zerosCol2` = 2 + 3 - 1 - 0 = 4 - diff\[1\]\[0\] = `onesRow1 + onesCol0 - zerosRow1 - zerosCol0` = 2 + 1 - 1 - 2 = 0 - diff\[1\]\[1\] = `onesRow1 + onesCol1 - zerosRow1 - zerosCol1` = 2 + 1 - 1 - 2 = 0 - diff\[1\]\[2\] = `onesRow1 + onesCol2 - zerosRow1 - zerosCol2` = 2 + 3 - 1 - 0 = 4 - diff\[2\]\[0\] = `onesRow2 + onesCol0 - zerosRow2 - zerosCol0` = 1 + 1 - 2 - 2 = -2 - diff\[2\]\[1\] = `onesRow2 + onesCol1 - zerosRow2 - zerosCol1` = 1 + 1 - 2 - 2 = -2 - diff\[2\]\[2\] = `onesRow2 + onesCol2 - zerosRow2 - zerosCol2` = 1 + 3 - 2 - 0 = 2 **Example 2:** **Input:** grid = \[\[1,1,1\],\[1,1,1\]\] **Output:** \[\[5,5,5\],\[5,5,5\]\] **Explanation:** - diff\[0\]\[0\] = onesRow0 + onesCol0 - zerosRow0 - zerosCol0 = 3 + 2 - 0 - 0 = 5 - diff\[0\]\[1\] = onesRow0 + onesCol1 - zerosRow0 - zerosCol1 = 3 + 2 - 0 - 0 = 5 - diff\[0\]\[2\] = onesRow0 + onesCol2 - zerosRow0 - zerosCol2 = 3 + 2 - 0 - 0 = 5 - diff\[1\]\[0\] = onesRow1 + onesCol0 - zerosRow1 - zerosCol0 = 3 + 2 - 0 - 0 = 5 - diff\[1\]\[1\] = onesRow1 + onesCol1 - zerosRow1 - zerosCol1 = 3 + 2 - 0 - 0 = 5 - diff\[1\]\[2\] = onesRow1 + onesCol2 - zerosRow1 - zerosCol2 = 3 + 2 - 0 - 0 = 5 **Constraints:** * `m == grid.length` * `n == grid[i].length` * `1 <= m, n <= 105` * `1 <= m * n <= 105` * `grid[i][j]` is either `0` or `1`.

EASIEST SOLUTION WITH TLE OPTIMIZATION

difference-between-ones-and-zeros-in-row-and-column

# Intuition\n To optimize the solution and avoid Time Limit Exceeded (TLE), you can precompute the sums for rows and columns separately before calculating the difference matrix. This way, you avoid recalculating the sums for each element in the grid.\n\n\n\n# Code\n```\nclass Solution:\n def onesMinusZeros(self, grid: List[List[int]]) -> List[List[int]]:\n m,n=len(grid),len(grid[0])\n onesRow= [sum(row) for row in grid] \n onesCol= [sum(row[j] for row in grid) for j in range(n)]\n diff = [[0] * n for _ in range(m)]\n\n for i in range(m):\n for j in range(n):\n \n zerosRow= n-onesRow[i]\n zerosCol= m-onesCol[j]\n\n diff[i][j]=onesRow[i]+onesCol[j]-zerosRow-zerosCol\n return diff \n```\n# **PLEASE DO UPVOTE!!!\uD83E\uDD79**

You are given a **0-indexed** `m x n` binary matrix `grid`. A **0-indexed** `m x n` difference matrix `diff` is created with the following procedure: * Let the number of ones in the `ith` row be `onesRowi`. * Let the number of ones in the `jth` column be `onesColj`. * Let the number of zeros in the `ith` row be `zerosRowi`. * Let the number of zeros in the `jth` column be `zerosColj`. * `diff[i][j] = onesRowi + onesColj - zerosRowi - zerosColj` Return _the difference matrix_ `diff`. **Example 1:** **Input:** grid = \[\[0,1,1\],\[1,0,1\],\[0,0,1\]\] **Output:** \[\[0,0,4\],\[0,0,4\],\[-2,-2,2\]\] **Explanation:** - diff\[0\]\[0\] = `onesRow0 + onesCol0 - zerosRow0 - zerosCol0` = 2 + 1 - 1 - 2 = 0 - diff\[0\]\[1\] = `onesRow0 + onesCol1 - zerosRow0 - zerosCol1` = 2 + 1 - 1 - 2 = 0 - diff\[0\]\[2\] = `onesRow0 + onesCol2 - zerosRow0 - zerosCol2` = 2 + 3 - 1 - 0 = 4 - diff\[1\]\[0\] = `onesRow1 + onesCol0 - zerosRow1 - zerosCol0` = 2 + 1 - 1 - 2 = 0 - diff\[1\]\[1\] = `onesRow1 + onesCol1 - zerosRow1 - zerosCol1` = 2 + 1 - 1 - 2 = 0 - diff\[1\]\[2\] = `onesRow1 + onesCol2 - zerosRow1 - zerosCol2` = 2 + 3 - 1 - 0 = 4 - diff\[2\]\[0\] = `onesRow2 + onesCol0 - zerosRow2 - zerosCol0` = 1 + 1 - 2 - 2 = -2 - diff\[2\]\[1\] = `onesRow2 + onesCol1 - zerosRow2 - zerosCol1` = 1 + 1 - 2 - 2 = -2 - diff\[2\]\[2\] = `onesRow2 + onesCol2 - zerosRow2 - zerosCol2` = 1 + 3 - 2 - 0 = 2 **Example 2:** **Input:** grid = \[\[1,1,1\],\[1,1,1\]\] **Output:** \[\[5,5,5\],\[5,5,5\]\] **Explanation:** - diff\[0\]\[0\] = onesRow0 + onesCol0 - zerosRow0 - zerosCol0 = 3 + 2 - 0 - 0 = 5 - diff\[0\]\[1\] = onesRow0 + onesCol1 - zerosRow0 - zerosCol1 = 3 + 2 - 0 - 0 = 5 - diff\[0\]\[2\] = onesRow0 + onesCol2 - zerosRow0 - zerosCol2 = 3 + 2 - 0 - 0 = 5 - diff\[1\]\[0\] = onesRow1 + onesCol0 - zerosRow1 - zerosCol0 = 3 + 2 - 0 - 0 = 5 - diff\[1\]\[1\] = onesRow1 + onesCol1 - zerosRow1 - zerosCol1 = 3 + 2 - 0 - 0 = 5 - diff\[1\]\[2\] = onesRow1 + onesCol2 - zerosRow1 - zerosCol2 = 3 + 2 - 0 - 0 = 5 **Constraints:** * `m == grid.length` * `n == grid[i].length` * `1 <= m, n <= 105` * `1 <= m * n <= 105` * `grid[i][j]` is either `0` or `1`.

Solving from a brute force base case to an efficient solution

difference-between-ones-and-zeros-in-row-and-column

# Intuition\n\nBase case- for a given cell we need the row and we need the column. \n\nSecond look- For each row in the data we will need the column computed many times, so let\'s pre-compute all of the rows. \n\nThird look- We are returning a matrix identical to the input matrix and we aren\'t re-iterating over cells since we\'ve pre-computed the column values. When I shifted from having a response matrix that was different from the input to just re-purposing the input my memory utilization cut down from 61MB to 43MB and brought me into the top 90% of users for memory optimization. This change also brought me from the bottom 5% of users for computational time to the top 57%. \n\nFourth Look- The computational score bothered me, but I figured adding to the stack and processing the helper method took time, so I removed it and just used the built in count() method.... that brought my computational score from beats 57% to beats 94% of users.\n\n\n# Approach\n\nOriginally I made a method to solve the base case:\n\n```\n def solveBaseCase(self, row):\n count_ones = 0\n count_zeroes = 0\n for entry in row:\n if entry == 0:\n count_zeroes += 1\n if entry == 1:\n count_ones += 1\n return (count_zeroes, count_ones)\n```\n\nThen I remembered we can use python\'s built in count function. Interestingly when I removed the helper method the time only marginally improved, suggesting that the helper method might be useful in production for code readability and future maintenance.\n\nThe `zip(*grid)` syntax is something super useful as it inverts matrices, it makes rows into columns for easy use. We can proof that it is immutable with `list(zip(*list(zip(*grid))))` which will return an object that looks like the original grid matrix.\n\n\n\n\n# Code\n```\nclass Solution: \n def onesMinusZeros(self, grid: List[List[int]]) -> List[List[int]]:\n cols_solved = [(c.count(0), c.count(1)) for c in zip(*grid)]\n for i in range(len(grid)):\n zeroes_x, ones_x = (grid[i].count(0), grid[i].count(1))\n for j in range(len(cols_solved)):\n zeroes_y, ones_y = cols_solved[j]\n grid[i][j] = ones_x + ones_y - zeroes_x - zeroes_y\n return grid\n```\n\nMy original code which exceeded time limit:\n\n```\ndef solveBaseCase(self, row):\n count_ones = 0\n count_zeroes = 0\n for entry in row:\n if entry == 0:\n count_zeroes += 1\n if entry == 1:\n count_ones += 1\n return (count_zeroes, count_ones)\n \n\n def onesMinusZeros(self, grid: List[List[int]]) -> List[List[int]]:\n diff = copy.deepcopy(grid)\n cols = [c for i, c in enumerate(zip(*grid))]\n for i in range(len(grid)):\n zeroes_x, ones_x = self.solveBaseCase(grid[i])\n for j in range(len(cols)):\n zeroes_y, ones_y = self.solveBaseCase(cols[j])\n diff[i][j] = ones_x + ones_y - zeroes_x - zeroes_y\n return diff\n```\n\nNote- when I precomputed the columns with the following change the code passed within time:\n\n```\ndef onesMinusZeros(self, grid: List[List[int]]) -> List[List[int]]:\n diff = copy.deepcopy(grid)\n cols = [c for i, c in enumerate(zip(*grid))]\n cols_solved = []\n for j in range(len(cols)):\n cols_solved.append(self.solveBaseCase(cols[j]))\n for i in range(len(grid)):\n zeroes_x, ones_x = self.solveBaseCase(grid[i])\n for j in range(len(cols)):\n zeroes_y, ones_y = cols_solved[j]\n diff[i][j] = ones_x + ones_y - zeroes_x - zeroes_y\n return diff\n```

You are given a **0-indexed** `m x n` binary matrix `grid`. A **0-indexed** `m x n` difference matrix `diff` is created with the following procedure: * Let the number of ones in the `ith` row be `onesRowi`. * Let the number of ones in the `jth` column be `onesColj`. * Let the number of zeros in the `ith` row be `zerosRowi`. * Let the number of zeros in the `jth` column be `zerosColj`. * `diff[i][j] = onesRowi + onesColj - zerosRowi - zerosColj` Return _the difference matrix_ `diff`. **Example 1:** **Input:** grid = \[\[0,1,1\],\[1,0,1\],\[0,0,1\]\] **Output:** \[\[0,0,4\],\[0,0,4\],\[-2,-2,2\]\] **Explanation:** - diff\[0\]\[0\] = `onesRow0 + onesCol0 - zerosRow0 - zerosCol0` = 2 + 1 - 1 - 2 = 0 - diff\[0\]\[1\] = `onesRow0 + onesCol1 - zerosRow0 - zerosCol1` = 2 + 1 - 1 - 2 = 0 - diff\[0\]\[2\] = `onesRow0 + onesCol2 - zerosRow0 - zerosCol2` = 2 + 3 - 1 - 0 = 4 - diff\[1\]\[0\] = `onesRow1 + onesCol0 - zerosRow1 - zerosCol0` = 2 + 1 - 1 - 2 = 0 - diff\[1\]\[1\] = `onesRow1 + onesCol1 - zerosRow1 - zerosCol1` = 2 + 1 - 1 - 2 = 0 - diff\[1\]\[2\] = `onesRow1 + onesCol2 - zerosRow1 - zerosCol2` = 2 + 3 - 1 - 0 = 4 - diff\[2\]\[0\] = `onesRow2 + onesCol0 - zerosRow2 - zerosCol0` = 1 + 1 - 2 - 2 = -2 - diff\[2\]\[1\] = `onesRow2 + onesCol1 - zerosRow2 - zerosCol1` = 1 + 1 - 2 - 2 = -2 - diff\[2\]\[2\] = `onesRow2 + onesCol2 - zerosRow2 - zerosCol2` = 1 + 3 - 2 - 0 = 2 **Example 2:** **Input:** grid = \[\[1,1,1\],\[1,1,1\]\] **Output:** \[\[5,5,5\],\[5,5,5\]\] **Explanation:** - diff\[0\]\[0\] = onesRow0 + onesCol0 - zerosRow0 - zerosCol0 = 3 + 2 - 0 - 0 = 5 - diff\[0\]\[1\] = onesRow0 + onesCol1 - zerosRow0 - zerosCol1 = 3 + 2 - 0 - 0 = 5 - diff\[0\]\[2\] = onesRow0 + onesCol2 - zerosRow0 - zerosCol2 = 3 + 2 - 0 - 0 = 5 - diff\[1\]\[0\] = onesRow1 + onesCol0 - zerosRow1 - zerosCol0 = 3 + 2 - 0 - 0 = 5 - diff\[1\]\[1\] = onesRow1 + onesCol1 - zerosRow1 - zerosCol1 = 3 + 2 - 0 - 0 = 5 - diff\[1\]\[2\] = onesRow1 + onesCol2 - zerosRow1 - zerosCol2 = 3 + 2 - 0 - 0 = 5 **Constraints:** * `m == grid.length` * `n == grid[i].length` * `1 <= m, n <= 105` * `1 <= m * n <= 105` * `grid[i][j]` is either `0` or `1`.

✔Beats 100% || 🔥Mind Blowing Technique || 🔥With Picture || Detail explanations

minimum-penalty-for-a-shop

\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n> For every hour when the shop is open and no customers come, the penalty increases by 1.\nFor every hour when the shop is closed and customers come, the penalty increases by 1.\n\nConsider the case where we close the shop at the `i`^th hour with `iPenalty` and at the `j`^th hour with `jPenalty`(`i` < `j`).\nThe intuition is that the difference between `iPenalty` and `jPenalty`, aka `jPenalty - iPenalty`\uFF0C is only related to `customers[i...j-1]`. The rest doesn\'t matter.\n\nWhether we close the shop at the `i`^th or `j`^th hour, the penalties of both would have to count for the number of `N`s in `customers[0, i - 1]` and `Y`s in `customers[j, n - 1]`. \n***Therefore the difference(`jPenalty - iPenalty`) is just the number of `N`s minus the number of `Y`s in `customers[i, j - 1]`.***\nA Further explanation would be: `iPenalty` would have to count for the number of `Y`s in `customers[i, j - 1]`, while `jPenalty` would have to count for the number of `N`s in `customers[i, j - 1]`.\nNow, if the difference (`jPenalty - iPenalty`) is less than zero, it means `jPenalty` is less than `iPenalty`. In other words, it\'s better to close the shop at the `j`^th hour than at the `i`^th hour.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. First we assume we close the shop at the `0`^th hour.\nSet `bestTime = 0` and `penaltyDiff = 0`\n2. Iterate through `customers`, for the `i`^th character:\n - If `customers[i] == \'Y\'`, decrement `penaltyDiff` by 1. Otherwise, increment `penaltyDiff` by 1.\n - If `penaltyDiff < 0`, set `bestTime = i + 1` and `penaltyDiff = 0`\n1. Return `bestTime` after the iteration.\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int bestClosingTime(String customers) {\n char[] chars = customers.toCharArray();\n int bestTime = 0, penaltyDiff = 0;\n\n for (int i = 0; i < chars.length; i++) {\n if (chars[i] == \'Y\') penaltyDiff--;\n else penaltyDiff++;\n\n if (penaltyDiff < 0) {\n penaltyDiff = 0;\n bestTime = i + 1;\n }\n }\n return bestTime;\n }\n}\n\n```\n```python []\nclass Solution:\n def bestClosingTime(self, customers: str) -> int:\n bestTime, penaltyDiff = 0, 0\n \n for i in range(0, len(customers)):\n if customers[i] == \'Y\':\n penaltyDiff -= 1\n else:\n penaltyDiff += 1\n \n if penaltyDiff < 0:\n penaltyDiff = 0;\n bestTime = i + 1;\n return bestTime;\n```\n```c []\nint bestClosingTime(char * customers){\n int bestTime = 0, penaltyDiff = 0;\n\n for (int i = 0, len = strlen(customers); i < len; i++) {\n if (customers[i] == \'Y\') penaltyDiff--;\n else penaltyDiff++;\n\n if (penaltyDiff < 0) {\n penaltyDiff = 0;\n bestTime = i + 1;\n }\n }\n return bestTime;\n}\n```\n```C++ []\nclass Solution {\npublic:\n int bestClosingTime(string customers) {\n int bestTime = 0, penaltyDiff = 0;\n \n for (int i = 0, len = customers.length(); i < len; i++) {\n if (customers[i] == \'Y\') penaltyDiff--;\n else penaltyDiff++;\n \n if (penaltyDiff < 0) {\n penaltyDiff = 0;\n bestTime = i + 1;\n }\n }\n return bestTime;\n }\n};\n```\n```javascript []\nvar bestClosingTime = function(customers) {\n var bestTime = 0, penaltyDiff = 0;\n\n for (var i = 0; i < customers.length; i++) {\n if (customers[i] == \'Y\') penaltyDiff--;\n else penaltyDiff++;\n\n if (penaltyDiff < 0) {\n penaltyDiff = 0;\n bestTime = i + 1;\n }\n }\n return bestTime;\n};\n```\n

You are given the customer visit log of a shop represented by a **0-indexed** string `customers` consisting only of characters `'N'` and `'Y'`: * if the `ith` character is `'Y'`, it means that customers come at the `ith` hour * whereas `'N'` indicates that no customers come at the `ith` hour. If the shop closes at the `jth` hour (`0 <= j <= n`), the **penalty** is calculated as follows: * For every hour when the shop is open and no customers come, the penalty increases by `1`. * For every hour when the shop is closed and customers come, the penalty increases by `1`. Return _the **earliest** hour at which the shop must be closed to incur a **minimum** penalty._ **Note** that if a shop closes at the `jth` hour, it means the shop is closed at the hour `j`. **Example 1:** **Input:** customers = "YYNY " **Output:** 2 **Explanation:** - Closing the shop at the 0th hour incurs in 1+1+0+1 = 3 penalty. - Closing the shop at the 1st hour incurs in 0+1+0+1 = 2 penalty. - Closing the shop at the 2nd hour incurs in 0+0+0+1 = 1 penalty. - Closing the shop at the 3rd hour incurs in 0+0+1+1 = 2 penalty. - Closing the shop at the 4th hour incurs in 0+0+1+0 = 1 penalty. Closing the shop at 2nd or 4th hour gives a minimum penalty. Since 2 is earlier, the optimal closing time is 2. **Example 2:** **Input:** customers = "NNNNN " **Output:** 0 **Explanation:** It is best to close the shop at the 0th hour as no customers arrive. **Example 3:** **Input:** customers = "YYYY " **Output:** 4 **Explanation:** It is best to close the shop at the 4th hour as customers arrive at each hour. **Constraints:** * `1 <= customers.length <= 105` * `customers` consists only of characters `'Y'` and `'N'`.

【Video】Time : O(n) Space: O(1) with Python, JavaScript, Java and C++

minimum-penalty-for-a-shop

# Intuition\nThe main point of this code is to determine the best closing time for a shop based on customer visit records. It calculates the optimal time to close the shop such that if there are any customers inside, the shop closes at the next hour. The code iterates through the customer records, maintaining a counter (customer_left) to track the difference between incoming and departing customers. It updates the result (res) whenever the condition of having customers inside (customer_left > 0) is met, indicating that the shop should close at the next hour.\n\nThis python solution beats 98%.\n\n\n\n---\n\n\n# Solution Video\n\n### Please subscribe to my channel from here. I have 251 videos as of August 29th, 2023.\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nhttps://youtu.be/KB4ZPkw9IsA\n\n### In the video, the steps of approach below are visualized using diagrams and drawings. I\'m sure you understand the solution easily!\n---\n\n# Approach\nThis is based on Python. Other might be different a bit.\n\n1. Initialize variables:\n - `res`: To store the best closing time (initially set to 0).\n - `customer_left`: To keep track of the difference between customers who came in and customers who left (initially set to 0).\n\n2. Loop through the `customers` string using an index `i`:\n - For each index `i`:\n - Check if the current customer is coming in (\'Y\'):\n - Increment `customer_left` by 1 to account for the incoming customer.\n\n3. Check if customers are still inside the shop:\n - If `customer_left` is greater than 0 (meaning there are still customers inside):\n - Update `res` with the current index `i + 1` (since we\'re 0-indexed and the result needs to be 1-indexed).\n - Reset `customer_left` to 0 to indicate that all customers are accounted for.\n\n4. If the current customer is not coming in (\'N\'):\n - Decrement `customer_left` by 1 to account for the departing customer.\n\n5. After iterating through all customers:\n - Return the calculated `res`, which represents the best closing time to minimize the penalty.\n\n# Complexity\n- Time complexity: O(n)\n\n\n- Space complexity: O(1)\n\n```python []\nclass Solution:\n def bestClosingTime(self, customers: str) -> int:\n res = 0\n customer_left = 0\n \n for i in range(len(customers)):\n if customers[i] == \'Y\':\n customer_left += 1\n\n if customer_left > 0:\n res = i + 1\n customer_left = 0 \n else:\n customer_left -= 1\n \n return res\n\n```\n```javascript []\nvar bestClosingTime = function(customers) {\n let res = 0;\n let customerLeft = 0;\n\n for (let i = 0; i < customers.length; i++) {\n if (customers[i] === \'Y\') {\n customerLeft++;\n\n if (customerLeft > 0) {\n res = i + 1;\n customerLeft = 0;\n }\n } else {\n customerLeft--;\n }\n }\n\n return res; \n};\n```\n```java []\nclass Solution {\n public int bestClosingTime(String customers) {\n int res = 0;\n int customerLeft = 0;\n\n for (int i = 0; i < customers.length(); i++) {\n if (customers.charAt(i) == \'Y\') {\n customerLeft++;\n\n if (customerLeft > 0) {\n res = i + 1;\n customerLeft = 0;\n }\n } else {\n customerLeft--;\n }\n }\n\n return res; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int bestClosingTime(string customers) {\n int res = 0;\n int customerLeft = 0;\n\n for (int i = 0; i < customers.length(); i++) {\n if (customers[i] == \'Y\') {\n customerLeft++;\n\n if (customerLeft > 0) {\n res = i + 1;\n customerLeft = 0;\n }\n } else {\n customerLeft--;\n }\n }\n\n return res; \n }\n};\n```\n

You are given the customer visit log of a shop represented by a **0-indexed** string `customers` consisting only of characters `'N'` and `'Y'`: * if the `ith` character is `'Y'`, it means that customers come at the `ith` hour * whereas `'N'` indicates that no customers come at the `ith` hour. If the shop closes at the `jth` hour (`0 <= j <= n`), the **penalty** is calculated as follows: * For every hour when the shop is open and no customers come, the penalty increases by `1`. * For every hour when the shop is closed and customers come, the penalty increases by `1`. Return _the **earliest** hour at which the shop must be closed to incur a **minimum** penalty._ **Note** that if a shop closes at the `jth` hour, it means the shop is closed at the hour `j`. **Example 1:** **Input:** customers = "YYNY " **Output:** 2 **Explanation:** - Closing the shop at the 0th hour incurs in 1+1+0+1 = 3 penalty. - Closing the shop at the 1st hour incurs in 0+1+0+1 = 2 penalty. - Closing the shop at the 2nd hour incurs in 0+0+0+1 = 1 penalty. - Closing the shop at the 3rd hour incurs in 0+0+1+1 = 2 penalty. - Closing the shop at the 4th hour incurs in 0+0+1+0 = 1 penalty. Closing the shop at 2nd or 4th hour gives a minimum penalty. Since 2 is earlier, the optimal closing time is 2. **Example 2:** **Input:** customers = "NNNNN " **Output:** 0 **Explanation:** It is best to close the shop at the 0th hour as no customers arrive. **Example 3:** **Input:** customers = "YYYY " **Output:** 4 **Explanation:** It is best to close the shop at the 4th hour as customers arrive at each hour. **Constraints:** * `1 <= customers.length <= 105` * `customers` consists only of characters `'Y'` and `'N'`.

✅ 99.70% 2-Approach Single Pass & Prefix Sum

minimum-penalty-for-a-shop

# Interview Guide: Minimum Penalty for a Shop\n\n## Problem Understanding\n\n**Description**: \nSo, you\'re ramping up for coding interviews or just looking to sharpen your algorithmic skills, right? Well, the "Minimum Penalty for a Shop" problem is a perfect starting point. Imagine owning a shop and you need to decide when to close it. You have a log of \'Y\'s and \'N\'s, indicating customer visits and no-shows. Your goal? Find that sweet spot\u2014the earliest time to close and minimize penalties.\n\n## Interview Preparation Tips & Considerations\n\n### 1. **Don\'t Skim Over Constraints** \n - First, note that the log can be lengthy, up to $$10^5$$ characters. This tells you that your solution must be optimized to handle large inputs efficiently.\n - Secondly, the log contains only \'Y\' and \'N\'. This simplicity is deceptive; the challenge lies in optimizing your approach.\n\n### 2. **Approach Selection: Your First Critical Decision**\n - **Single Pass**: If time complexity is your main concern, this approach should be your go-to. It runs in $$O(n)$$ time and uses a minuscule $$O(1)$$ space. This is ideal for interviews where time is of the essence.\n \n - **Prefix-Suffix Sums**: Opt for this if you have more freedom with space. It also operates in $$O(n)$$ time but uses $$O(n)$$ space. This approach provides a more in-depth understanding of the log.\n\n### How to Start Coding? \n1. **Understand the Problem**: Before you even touch the keyboard, make sure you understand what the problem is asking. Do a dry run with a sample input.\n \n2. **Choose Your Approach**: Based on the problem constraints and what you\'re comfortable with, select an approach. Each has its merits and demerits.\n\n3. **Pseudocode First**: Write down a quick pseudocode to outline your thoughts. It helps to see the logic on paper before coding.\n\n4. **Code and Test**: Now, dive into the code. Keep testing at every significant step to ensure you\'re on the right track.\n\n5. **Edge Cases**: Don\'t forget them; they\'re the Achilles heel in coding interviews. Make sure your solution handles all edge cases.\n\n6. **Review**: Before saying you\'re done, review the code for any possible optimizations or errors. \n\n---\n\n# More than Live Coding:\nhttps://youtu.be/Za91oxv7uls?si=VYY0Fxj9NxpY1WkF\n\n---\n\n# Single Pass Approach\n\n## Explanation\n\nThe logic behind the Single Pass Approach is to efficiently iterate through the customer visit log string once, while keeping track of the penalty score. This way, we can find the optimal time to close the shop with minimal computational overhead. Here\'s a detailed explanation:\n\n### 1. **Initialization**: \nWe start by initializing three variables: `max_score`, `score`, and `best_hour` to 0. \n- `max_score`: To keep track of the highest score seen so far.\n- `score`: To hold the current penalty score.\n- `best_hour`: To remember the hour where `max_score` occurred.\n\n```python\nmax_score = score = 0\nbest_hour = -1\n```\n\n### 2. **Iterate through the String**: \nHere comes the main part. We loop through each character `c` in the customer visit log string. We use a single variable `score` to keep track of the penalty.\n\n- If `c` is \'Y\': \n This means a customer is visiting the shop at this hour, so we increment `score` by 1. This is because if the shop were closed at this hour, it would incur a penalty.\n\n- If `c` is \'N\': \n No customer is visiting, so we decrement `score` by 1. This implies that keeping the shop open at this hour would be wasteful and result in a penalty.\n\n```python\nfor i, c in enumerate(customers):\n score += 1 if c == \'Y\' else -1\n```\n\n### 3. **Track Max Score and Best Hour**: \nAt each iteration, we compare `score` with `max_score`. If `score` is greater, it means we\'ve found a new optimal time to close the shop. So, we update `max_score` and set `best_hour` to the current index `i`.\n\n```python\n if score > max_score:\n max_score, best_hour = score, i\n```\n\n### 4. **Return Result**: \nFinally, we\'ve iterated through the entire string and found the optimal time to close the shop, which is stored in `best_hour`. We return `best_hour + 1` (because the question is 0-indexed).\n\n```python\nreturn best_hour + 1\n```\n\n## Complexity\n\n### Time Complexity: \nThe algorithm runs in $$ O(n) $$ time since we go through the string once.\n\n### Space Complexity: \nThe space complexity is $$ O(1) $$, as we use constant extra space.\n\n# Prefix-Suffix Sums Approach\n\n### Explanation\n\n1. **Initialization**: \n Initialize two empty arrays `prefixN` and `suffixY` with a leading zero. Initialize counters `cntN` and `cntY` to zero.\n\n2. **Compute Prefix Sums for \'N\'**: \n Traverse the string and update `prefixN` with the count of \'N\'s until the current index.\n\n3. **Compute Suffix Sums for \'Y\'**: \n Traverse the string in reverse and update `suffixY` with the count of \'Y\'s from the current index to the end.\n\n4. **Calculate Penalties**: \n Compute the penalty for each hour as `prefixN[i] + suffixY[i]`.\n\n5. **Find Minimum Penalty**: \n Identify the index with the minimum penalty.\n\n6. **Return Result**: \n Return the index as the best time to close the shop.\n\n### Complexity\n\n- **Time Complexity**: $$O(n)$$\n- **Space Complexity**: $$O(n)$$\n\n## Conclusion\n\nBoth approaches solve the problem effectively, each with its own advantages. The Single Pass approach is more space-efficient, while the Prefix-Suffix Sums approach is more intuitive. The choice between the two depends on whether space efficiency or ease of understanding is a higher priority.\n\n---\n\n# Performance Table \n\n## Single Pass\n\n| Language | Runtime (ms) | Memory (MB) |\n|--------------------|--------------|-------------|\n| Rust | 4 | 2.2 |\n| Go | 7 | 5.6 |\n| Java | 9 | 43.9 |\n| C++ | 23 | 10.7 |\n| PHP | 29 | 19.9 |\n| Python3 (Single Pass) | 74 | 17.4 |\n| JavaScript | 65 | 44.7 |\n| C# | 70 | 42.2 |\n| Python3 (Prefix) | 228 | 25.8 |\n\nThe table reveals how the Single Pass approach in Python significantly outperforms the Prefix approach, underscoring the importance of algorithmic optimization. It also offers a fascinating look at the performance variations across different programming languages.\n\n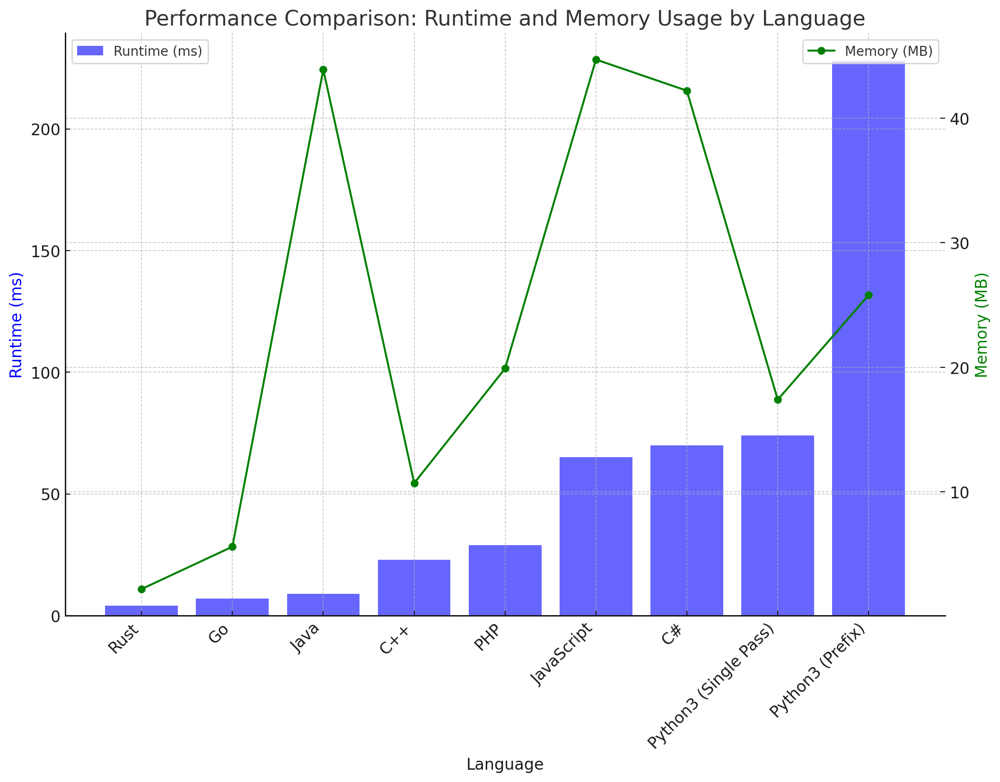\n\n---\n\n# Code Single Pass\n``` Python []\nclass Solution:\n def bestClosingTime(self, customers: str) -> int:\n max_score = score = 0\n best_hour = -1\n\n for i, c in enumerate(customers):\n score += 1 if c == \'Y\' else -1\n if score > max_score:\n max_score, best_hour = score, i\n \n return best_hour + 1\n\n```\n``` C++ []\nclass Solution {\npublic:\n int bestClosingTime(string customers) {\n int max_score = 0, score = 0, best_hour = -1;\n for(int i = 0; i < customers.size(); ++i) {\n score += (customers[i] == \'Y\') ? 1 : -1;\n if(score > max_score) {\n max_score = score;\n best_hour = i;\n }\n }\n return best_hour + 1;\n }\n};\n```\n``` Go []\nfunc bestClosingTime(customers string) int {\n max_score, score, best_hour := 0, 0, -1\n for i := 0; i < len(customers); i++ {\n if customers[i] == \'Y\' {\n score++\n } else {\n score--\n }\n if score > max_score {\n max_score = score\n best_hour = i\n }\n }\n return best_hour + 1\n}\n```\n``` Rust []\nimpl Solution {\n pub fn best_closing_time(customers: String) -> i32 {\n let mut max_score = 0;\n let mut score = 0;\n let mut best_hour = -1;\n \n for (i, c) in customers.chars().enumerate() {\n if c == \'Y\' {\n score += 1;\n } else {\n score -= 1;\n }\n \n if score > max_score {\n max_score = score;\n best_hour = i as i32;\n }\n }\n \n best_hour + 1\n }\n}\n```\n``` Java []\npublic class Solution {\n public int bestClosingTime(String customers) {\n int max_score = 0, score = 0, best_hour = -1;\n for(int i = 0; i < customers.length(); ++i) {\n score += (customers.charAt(i) == \'Y\') ? 1 : -1;\n if(score > max_score) {\n max_score = score;\n best_hour = i;\n }\n }\n return best_hour + 1;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {string} customers\n * @return {number}\n */\nvar bestClosingTime = function(customers) {\n let max_score = 0, score = 0, best_hour = -1;\n for(let i = 0; i < customers.length; ++i) {\n score += (customers[i] === \'Y\') ? 1 : -1;\n if(score > max_score) {\n max_score = score;\n best_hour = i;\n }\n }\n return best_hour + 1;\n};\n```\n``` PHP []\nclass Solution {\n public function bestClosingTime($customers) {\n $max_score = $score = 0;\n $best_hour = -1;\n \n for($i = 0; $i < strlen($customers); ++$i) {\n $score += ($customers[$i] === \'Y\') ? 1 : -1;\n if($score > $max_score) {\n $max_score = $score;\n $best_hour = $i;\n }\n }\n \n return $best_hour + 1;\n }\n}\n```\n``` C# []\npublic class Solution {\n public int BestClosingTime(string customers) {\n int max_score = 0, score = 0, best_hour = -1;\n for(int i = 0; i < customers.Length; ++i) {\n score += (customers[i] == \'Y\') ? 1 : -1;\n if(score > max_score) {\n max_score = score;\n best_hour = i;\n }\n }\n return best_hour + 1;\n }\n}\n```\n\n# Code Prefix Sums\n``` Python []\nclass Solution:\n def bestClosingTime(self, customers: str) -> int:\n n, cntN, cntY = len(customers), 0, 0\n prefixN, suffixY = [0], [0]\n \n for c in customers:\n cntN += (c == \'N\')\n prefixN.append(cntN)\n \n for c in reversed(customers):\n cntY += (c == \'Y\')\n suffixY.append(cntY)\n \n suffixY.reverse()\n \n best_hour, _ = min(enumerate(a + b for a, b in zip(prefixN, suffixY)), key=lambda x: x[1])\n \n return best_hour\n```\n\nEvery line of code you write brings you one step closer to becoming an expert. Both brevity and clarity have their merits in coding. So keep exploring and don\'t hesitate to share your unique perspective. You never know, your insight might just be the \'aha\' moment someone else needs. Happy Coding! \uD83D\uDE80\uD83D\uDCA1

You are given the customer visit log of a shop represented by a **0-indexed** string `customers` consisting only of characters `'N'` and `'Y'`: * if the `ith` character is `'Y'`, it means that customers come at the `ith` hour * whereas `'N'` indicates that no customers come at the `ith` hour. If the shop closes at the `jth` hour (`0 <= j <= n`), the **penalty** is calculated as follows: * For every hour when the shop is open and no customers come, the penalty increases by `1`. * For every hour when the shop is closed and customers come, the penalty increases by `1`. Return _the **earliest** hour at which the shop must be closed to incur a **minimum** penalty._ **Note** that if a shop closes at the `jth` hour, it means the shop is closed at the hour `j`. **Example 1:** **Input:** customers = "YYNY " **Output:** 2 **Explanation:** - Closing the shop at the 0th hour incurs in 1+1+0+1 = 3 penalty. - Closing the shop at the 1st hour incurs in 0+1+0+1 = 2 penalty. - Closing the shop at the 2nd hour incurs in 0+0+0+1 = 1 penalty. - Closing the shop at the 3rd hour incurs in 0+0+1+1 = 2 penalty. - Closing the shop at the 4th hour incurs in 0+0+1+0 = 1 penalty. Closing the shop at 2nd or 4th hour gives a minimum penalty. Since 2 is earlier, the optimal closing time is 2. **Example 2:** **Input:** customers = "NNNNN " **Output:** 0 **Explanation:** It is best to close the shop at the 0th hour as no customers arrive. **Example 3:** **Input:** customers = "YYYY " **Output:** 4 **Explanation:** It is best to close the shop at the 4th hour as customers arrive at each hour. **Constraints:** * `1 <= customers.length <= 105` * `customers` consists only of characters `'Y'` and `'N'`.

Python Solution using prefix sum and dictionary

minimum-penalty-for-a-shop

\n# Code\n```\nclass Solution:\n def bestClosingTime(self, customers: str) -> int:\n\n d = {i : 1e9 for i in range(len(customers)+1)}\n yp = [0 for i in range(len(customers))]\n np = [0 for i in range(len(customers))]\n\n for i in range(len(customers)) :\n if customers[i] == "Y" :\n yp[i] += yp[i-1] + 1 \n else :\n yp[i] = yp[i-1]\n if customers[i] == "N" :\n np[i] += np[i-1] + 1 \n else:\n np[i] = np[i-1]\n \n yp = [0] + yp\n np = [0] + np\n\n d[yp[-1]] = 0\n\n for i in range(1,len(customers)+1) :\n val = yp[-1] - yp[i]\n val += np[i]\n\n d[val] = min(d[val] , i )\n\n dic = {}\n for k,v in d.items():\n if v !=1e9:\n dic[k] = v \n\n dic = dict(sorted(dic.items() , key = lambda x : x[0]))\n\n for k,v in dic.items():\n return v\n```

You are given the customer visit log of a shop represented by a **0-indexed** string `customers` consisting only of characters `'N'` and `'Y'`: * if the `ith` character is `'Y'`, it means that customers come at the `ith` hour * whereas `'N'` indicates that no customers come at the `ith` hour. If the shop closes at the `jth` hour (`0 <= j <= n`), the **penalty** is calculated as follows: * For every hour when the shop is open and no customers come, the penalty increases by `1`. * For every hour when the shop is closed and customers come, the penalty increases by `1`. Return _the **earliest** hour at which the shop must be closed to incur a **minimum** penalty._ **Note** that if a shop closes at the `jth` hour, it means the shop is closed at the hour `j`. **Example 1:** **Input:** customers = "YYNY " **Output:** 2 **Explanation:** - Closing the shop at the 0th hour incurs in 1+1+0+1 = 3 penalty. - Closing the shop at the 1st hour incurs in 0+1+0+1 = 2 penalty. - Closing the shop at the 2nd hour incurs in 0+0+0+1 = 1 penalty. - Closing the shop at the 3rd hour incurs in 0+0+1+1 = 2 penalty. - Closing the shop at the 4th hour incurs in 0+0+1+0 = 1 penalty. Closing the shop at 2nd or 4th hour gives a minimum penalty. Since 2 is earlier, the optimal closing time is 2. **Example 2:** **Input:** customers = "NNNNN " **Output:** 0 **Explanation:** It is best to close the shop at the 0th hour as no customers arrive. **Example 3:** **Input:** customers = "YYYY " **Output:** 4 **Explanation:** It is best to close the shop at the 4th hour as customers arrive at each hour. **Constraints:** * `1 <= customers.length <= 105` * `customers` consists only of characters `'Y'` and `'N'`.

Dynamic Customer Status Analysis for Optimal Closing Time

minimum-penalty-for-a-shop

# Intuition\nThe initial thoughts for solving this problem involve keeping track of the customers\' statuses (whether they are leaving or staying) and determining the optimal closing time based on the changes in these statuses.\n\n# Approach\nThe approach to solving the problem involves iterating through the customers\' statuses and maintaining a dynamic programming array dp that keeps track of the cumulative changes in the number of customers present at different times. The key idea is to count the number of customers who are still present at each time and the ones who have left.\n\nStarting with a base case, the initial value of dp[0] is set to the count of customers who plan to stay (\'Y\'). Then, as we iterate through the customers\' statuses, if a customer decides to leave (\'N\'), the value of dp[i+1] is updated to reflect one more customer present compared to the previous time. Conversely, if a customer decides to stay (\'Y\'), the value of dp[i+1] is updated to indicate one less customer present compared to the previous time.\n\nFinally, the index of the minimum value in the dp array represents the optimal closing time with the least number of remaining customers.\n\n# Complexity\n- Time complexity:\nThe solution iterates through the customers array once to compute the changes in the cumulative customer count, which takes linear time. Finding the index of the minimum value in the dp array also takes linear time. Therefore, the overall time complexity is O(n), where n is the length of the customers array.\n\n- Space complexity:\nThe solution uses an additional dp array to store cumulative changes in the customer count. Therefore, the space complexity is O(n), where n is the length of the customers array.\n\n# Code\n```\nclass Solution:\n def bestClosingTime(self, customers: str) -> int:\n n = len(customers)\n dp = [0] * (n+1)\n dp[0] = customers.count(\'Y\')\n for i in range(n):\n if customers[i] == \'N\':\n dp[i+1] = dp[i] + 1\n else:\n dp[i+1] = dp[i] - 1\n return dp.index(min(dp))\n```

You are given the customer visit log of a shop represented by a **0-indexed** string `customers` consisting only of characters `'N'` and `'Y'`: * if the `ith` character is `'Y'`, it means that customers come at the `ith` hour * whereas `'N'` indicates that no customers come at the `ith` hour. If the shop closes at the `jth` hour (`0 <= j <= n`), the **penalty** is calculated as follows: * For every hour when the shop is open and no customers come, the penalty increases by `1`. * For every hour when the shop is closed and customers come, the penalty increases by `1`. Return _the **earliest** hour at which the shop must be closed to incur a **minimum** penalty._ **Note** that if a shop closes at the `jth` hour, it means the shop is closed at the hour `j`. **Example 1:** **Input:** customers = "YYNY " **Output:** 2 **Explanation:** - Closing the shop at the 0th hour incurs in 1+1+0+1 = 3 penalty. - Closing the shop at the 1st hour incurs in 0+1+0+1 = 2 penalty. - Closing the shop at the 2nd hour incurs in 0+0+0+1 = 1 penalty. - Closing the shop at the 3rd hour incurs in 0+0+1+1 = 2 penalty. - Closing the shop at the 4th hour incurs in 0+0+1+0 = 1 penalty. Closing the shop at 2nd or 4th hour gives a minimum penalty. Since 2 is earlier, the optimal closing time is 2. **Example 2:** **Input:** customers = "NNNNN " **Output:** 0 **Explanation:** It is best to close the shop at the 0th hour as no customers arrive. **Example 3:** **Input:** customers = "YYYY " **Output:** 4 **Explanation:** It is best to close the shop at the 4th hour as customers arrive at each hour. **Constraints:** * `1 <= customers.length <= 105` * `customers` consists only of characters `'Y'` and `'N'`.

Simple solution with using Stack DS, beats 87%/92%

minimum-penalty-for-a-shop

# Intuition\nThe task description wants from us to find **the earliest hour**, that\'ll incur **a minimum penalty**.\n\n---\n\n\nLet\'s dive and obtain some facts:\n1. `Y` and `N` can be convert to bool `1` and `0`, respectively, if at `i`- th hour there\'re at least **1 customer** or not\n2. at each hour we want to calculate **a minimum penalty** as \n`sum of all zeros BEFORE the shop will closed`\n3. and at each step we need to somehow **manage the TOTAL** penalty\n```\ncustomers = [1, 1, 0, 1]\n# at i=0 step\ntotal = [1, 2, 2, 3]\n# or\ntotal = 3\n```\nIf you haven\'t already familiar with [prefix sum algorithm](https://en.wikipedia.org/wiki/Prefix_sum#:~:text=In%20computer%20science%2C%20the%20prefix,y0%20%3D%20x&text=y1%20%3D%20x0%20%2B%20x&text=y2%20%3D%20x0%20%2B%20x1%2B%20x), it\'s time to have a look.\n\n\n---\nTo be short, building of prefix sum is one of the easiest algorithm. Let\'s have a look for an example (pseudocode)\n```\n# if you have an array or list like\nA = [1, 2, 3, 4]\n\n# the prefix sum can be created as \n# 1. the total sum of elements\ntotal = sum(A)\n\n# 2. or iterating from i to n elements\nprefix = [A[0]]\n\nfor i in range of 1-n:\n add to prefix list sum of prefix[i - 1] + A[i]\n\n```\n\n# Approach\n1. initialize `cur` and `total` vars, that\'ll store initial amount of `Y`- s, and `ans` - variable with initial `0`\n2. iterate for all `customers` - collection\n3. add (`+1`) the particular penalty, if `customers[j] == \'N\'` or extract `-1`\n4. at each step check, if the `total` penalty is more than `cur` and replace `total` with the `cur` minimum, and `ans` with `j`\n5. return the `ans`\n\n# Complexity\n- Time complexity: **O(n)**, because of iterating over all `customers`\n\n- Space complexity: **O(1)**, because we don\'t use extra space.\n\n# Code\n```\nclass Solution:\n def bestClosingTime(self, customers: str) -> int:\n cur = total = customers.count(\'Y\')\n ans = 0\n\n for j in range(len(customers)):\n total += 1 if customers[j] == \'N\' else -1\n \n if total < cur:\n cur = total\n ans = j + 1\n\n return ans\n```

You are given the customer visit log of a shop represented by a **0-indexed** string `customers` consisting only of characters `'N'` and `'Y'`: * if the `ith` character is `'Y'`, it means that customers come at the `ith` hour * whereas `'N'` indicates that no customers come at the `ith` hour. If the shop closes at the `jth` hour (`0 <= j <= n`), the **penalty** is calculated as follows: * For every hour when the shop is open and no customers come, the penalty increases by `1`. * For every hour when the shop is closed and customers come, the penalty increases by `1`. Return _the **earliest** hour at which the shop must be closed to incur a **minimum** penalty._ **Note** that if a shop closes at the `jth` hour, it means the shop is closed at the hour `j`. **Example 1:** **Input:** customers = "YYNY " **Output:** 2 **Explanation:** - Closing the shop at the 0th hour incurs in 1+1+0+1 = 3 penalty. - Closing the shop at the 1st hour incurs in 0+1+0+1 = 2 penalty. - Closing the shop at the 2nd hour incurs in 0+0+0+1 = 1 penalty. - Closing the shop at the 3rd hour incurs in 0+0+1+1 = 2 penalty. - Closing the shop at the 4th hour incurs in 0+0+1+0 = 1 penalty. Closing the shop at 2nd or 4th hour gives a minimum penalty. Since 2 is earlier, the optimal closing time is 2. **Example 2:** **Input:** customers = "NNNNN " **Output:** 0 **Explanation:** It is best to close the shop at the 0th hour as no customers arrive. **Example 3:** **Input:** customers = "YYYY " **Output:** 4 **Explanation:** It is best to close the shop at the 4th hour as customers arrive at each hour. **Constraints:** * `1 <= customers.length <= 105` * `customers` consists only of characters `'Y'` and `'N'`.

[C++, Java, Python3] Counting Prefixes and Suffixes

count-palindromic-subsequences

# Intuition\nTo create a 5 digit palindrome we do not need to care about the middle element. We just need to find subsequence of pattern XY_YX. Calculate number of subsequences of type XY and subsequences of type YX around any given point `i` and multiply them to find number of subsequences of type XY_YX. Since string only has digits, the time complexity will be 100*n.\n\n# Approach\n* We will be maintaing the counts of digit in the list `cnts`\n* Keep 2 arrays pre and suf to store the number of prefixes of type XY and suffixes of type YX. `pre[i-1][1][2]` means prefixes of type `12` before index i. Similarly `suf[i+1][1][2]` means suffixes of type `21` after index i\n* Remember given string is made of digits that is `0123456789`. That\'s a total of 10 unique characters\n* Once we have calculated the prefix and suffix lists we just need to multiply `pre[i - 1][j][k]` with `suf[i + 1][j][k]` to find number of palindromic subsequences\n```\n for (int i = 0; i < n; i++) {\n int c = s[i] - \'0\';\n if (i) {\n for (int j = 0; j < 10; j++)\n for (int k = 0; k < 10; k++) {\n pre[i][j][k] = pre[i - 1][j][k];\n if (k == c) pre[i][j][k] += cnts[j];\n }\n }\n cnts[c]++;\n }\n```\n* Explanation of above code:\n * Use `if (i)` to not step outside of array limits when accessing `pre[i-1]`\n * Let\'s say `j = 5`, `k = 4` and `c = 4` which means we are looking at prefix `54`. `pre[i][j][k] = pre[i - 1][j][k]` will carry forward previous count of prefixes. Since `k == c` means the current character(s[i]) matches with last digit of prefix. To find total number of possibilites of prefixes of type `54` we need to know how many `5` exist before current index. This information is stored in `cnts[5]`. So we add `cnts[5]` to `pre[i][5][4]`.\n \n\n\n\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n\n# Code\n\n**Python 3**\n```\ndef countPalindromes(self, s: str) -> int:\n mod, n, ans = 10 ** 9 + 7, len(s), 0\n pre, cnts = [[[0] * 10 for _ in range(10)] for _ in range(n)], [0] * 10\n for i in range(n):\n c = ord(s[i]) - ord(\'0\')\n if i:\n for j in range(10):\n for k in range(10):\n pre[i][j][k] = pre[i - 1][j][k] \n if k == c: pre[i][j][k] += cnts[j]\n cnts[c] += 1\n suf, cnts = [[[0] * 10 for _ in range(10)] for _ in range(n)], [0] * 10\n for i in range(n - 1, -1, -1):\n c = ord(s[i]) - ord(\'0\')\n if i < n - 1:\n for j in range(10):\n for k in range(10):\n suf[i][j][k] = suf[i + 1][j][k]\n if k == c: suf[i][j][k] += cnts[j]\n cnts[c] += 1\n for i in range(2, n - 2):\n for j in range(10):\n for k in range(10):\n ans += pre[i - 1][j][k] * suf[i + 1][j][k]\n return ans % mod\n```\n\n**C++**\n```\nint pre[10000][10][10], suf[10000][10][10], cnts[10] = {};\nint countPalindromes(string s) {\n int mod = 1e9 + 7, n = s.size(), ans = 0;\n for (int i = 0; i < n; i++) {\n int c = s[i] - \'0\';\n if (i)\n for (int j = 0; j < 10; j++)\n for (int k = 0; k < 10; k++) {\n pre[i][j][k] = pre[i - 1][j][k];\n if (k == c) pre[i][j][k] += cnts[j];\n }\n cnts[c]++;\n }\n memset(cnts, 0, sizeof(cnts));\n for (int i = n - 1; i >= 0; i--) {\n int c = s[i] - \'0\';\n if (i < n - 1)\n for (int j = 0; j < 10; j++)\n for (int k = 0; k < 10; k++) {\n suf[i][j][k] = suf[i + 1][j][k];\n if (k == c) suf[i][j][k] += cnts[j];\n }\n cnts[c]++;\n }\n for (int i = 2; i < n - 2; i++)\n for (int j = 0; j < 10; j++)\n for (int k = 0; k < 10; k++)\n ans = (ans + 1LL * pre[i - 1][j][k] * suf[i + 1][j][k]) % mod;\n return ans;\n}\n```\n\n**Java**\n```\npublic int countPalindromes(String s) {\n int mod = 1000_000_007, n = s.length(), ans = 0, cnts[] = new int[10],\n pre[][][] = new int[n][10][10], suf[][][] = new int[n][10][10];\n for (int i = 0; i < n; i++) {\n int c = s.charAt(i) - \'0\';\n if (i > 0)\n for (int j = 0; j < 10; j++)\n for (int k = 0; k < 10; k++) {\n pre[i][j][k] = pre[i - 1][j][k];\n if (k == c) pre[i][j][k] += cnts[j];\n }\n cnts[c]++;\n }\n Arrays.fill(cnts, 0);\n for (int i = n - 1; i >= 0; i--) {\n int c = s.charAt(i) - \'0\';\n if (i < n - 1)\n for (int j = 0; j < 10; j++)\n for (int k = 0; k < 10; k++) {\n suf[i][j][k] = suf[i + 1][j][k];\n if (k == c) suf[i][j][k] += cnts[j];\n }\n cnts[c]++;\n }\n for (int i = 2; i < n - 2; i++)\n for (int j = 0; j < 10; j++)\n for (int k = 0; k < 10; k++)\n ans = (int)((ans + 1L * pre[i - 1][j][k] * suf[i + 1][j][k]) % mod);\n return ans;\n}\n```

Given a string of digits `s`, return _the number of **palindromic subsequences** of_ `s` _having length_ `5`. Since the answer may be very large, return it **modulo** `109 + 7`. **Note:** * A string is **palindromic** if it reads the same forward and backward. * A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. **Example 1:** **Input:** s = "103301 " **Output:** 2 **Explanation:** There are 6 possible subsequences of length 5: "10330 ", "10331 ", "10301 ", "10301 ", "13301 ", "03301 ". Two of them (both equal to "10301 ") are palindromic. **Example 2:** **Input:** s = "0000000 " **Output:** 21 **Explanation:** All 21 subsequences are "00000 ", which is palindromic. **Example 3:** **Input:** s = "9999900000 " **Output:** 2 **Explanation:** The only two palindromic subsequences are "99999 " and "00000 ". **Constraints:** * `1 <= s.length <= 104` * `s` consists of digits.

[C++|Java|Python3] short DP

count-palindromic-subsequences

Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/679b6a406693e67fb9637bbd1c8449f2372e76c5) for solutions of biweekly 92. \n\n**Intuition**\nIf a size 5 palindromic subsequence is given, we can check how many of it appears in s in O(N) via DP. In total, there are 100 (not 1000) relevant subsequences to check. \n\n**Implementation**\n**C++**\n```\nclass Solution {\npublic:\n int countPalindromes(string s) {\n const int mod = 1\'000\'000\'007; \n int n = s.size(); \n long ans = 0; \n for (int x = 0; x <= 9; ++x) \n for (int y = 0; y <= 9; ++y) {\n vector<int> pattern = {x, y, 0, y, x}; \n vector<long> dp(6); \n dp[5] = 1; \n for (int i = 0; i < n; ++i) \n for (int j = 0; j < 5; ++j) \n if (s[i] == pattern[j] + \'0\' || j == 2) dp[j] = (dp[j] + dp[j+1]) % mod; \n ans = (ans + dp[0]) % mod; \n }\n return ans; \n }\n};\n```\n**Java**\n```\nclass Solution {\n public int countPalindromes(String s) {\n final int mod = 1_000_000_007; \n long ans = 0; \n for (int x = 0; x <= 9; ++x) \n for (int y = 0; y <= 9; ++y) {\n int[] pattern = new int[] {x, y, 0, y, x};\n long [] dp = new long[6]; \n dp[5] = 1; \n for (int i = 0; i < s.length(); ++i) \n for (int j = 0; j < 5; ++j) \n if (s.charAt(i) == pattern[j] + \'0\' || j == 2) dp[j] = (dp[j] + dp[j+1]) % mod; \n ans = (ans + dp[0]) % mod; \n }\n return (int) ans; \n }\n}\n```\n**Python3**\n```\nclass Solution:\n def countPalindromes(self, s: str) -> int:\n ans = 0 \n for x in range(10): \n for y in range(10): \n pattern = f"{x}{y}|{y}{x}" \n dp = [0]*6\n dp[-1] = 1 \n for i in range(len(s)): \n for j in range(5): \n if s[i] == pattern[j] or j == 2: dp[j] += dp[j+1]\n ans = (ans + dp[0]) % 1_000_000_007\n return ans \n```\n**Complexity**\nTime O(N) \nSpace O(1)

Given a string of digits `s`, return _the number of **palindromic subsequences** of_ `s` _having length_ `5`. Since the answer may be very large, return it **modulo** `109 + 7`. **Note:** * A string is **palindromic** if it reads the same forward and backward. * A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. **Example 1:** **Input:** s = "103301 " **Output:** 2 **Explanation:** There are 6 possible subsequences of length 5: "10330 ", "10331 ", "10301 ", "10301 ", "13301 ", "03301 ". Two of them (both equal to "10301 ") are palindromic. **Example 2:** **Input:** s = "0000000 " **Output:** 21 **Explanation:** All 21 subsequences are "00000 ", which is palindromic. **Example 3:** **Input:** s = "9999900000 " **Output:** 2 **Explanation:** The only two palindromic subsequences are "99999 " and "00000 ". **Constraints:** * `1 <= s.length <= 104` * `s` consists of digits.

[Python3] Counting

count-palindromic-subsequences

**Biweekly Contest 92 Submission**\n\n**Counting**\n\n**Intuition**\n\nSince 5 is an odd length each *palindromic subsequences* must have a single middle element (\'3\' in the case of "10301"). Each *palindromic subsequences* must also have an ordered pair prior to a middle element with a mirrored ordered pair after ("10", "01" in the case of "10301"). The idea of this solution is to count the number of ordered pairs that mirror before and after each middle index (`index \u2208 [2, len(S) - 2)`).\n\n**Algorithm**\n1. If the length of the input string `S` is less than 5 no strings can be built of length 5 (return 0).\n2. Get the number of ordered pairs before and after each index.\n3. Count the number of matching pairs before and after each index. There are only 10 possible digits to loop through for each pair addition resulting in a global linear runtime.\n4. Return the value calculated modulo `10^9 + 7`.\n\n**Code**\n```Python3 []\nclass Solution:\n def countPalindromes(self, S: str) -> int:\n #Ignore string less than 5 characters (cannot have a 5 length substring)\n if len(S) < 5:\n return 0\n \n #Returns the running pair counts for each index\n def get_pairs(s):\n seen_cnt = {str(num):0 for num in range(10)}\n seen_cnt[s[0]] = 1 #We have seen the first character since we start the loop at 1\n pair_cnts = defaultdict(int)\n res = [None] #Filler empty dict (index = 0 / end index)\n \n #Getting running pairs\n for idx in range(1, len(s) - 1):\n res.append(pair_cnts.copy()) #Append running pair counts\n for num in seen_cnt.keys():\n pair_cnts[(num, s[idx])] += seen_cnt[num]\n seen_cnt[s[idx]] += 1\n \n #Filler empty dict (index = 0 / end index)\n res.append(None)\n \n return res\n \n res = 0\n #Getting post and pre pair counts\n pre, post = get_pairs(S), get_pairs(S[::-1])[::-1]\n \n #Check all possible middle characters -> S[2, len(S) - 2)\n for idx in range(2, len(S) - 2):\n for key, val in pre[idx].items():\n if key in post[idx]:\n res += post[idx][key] * val #Total pairs per key\n res %= 1000000007\n \n return res \n```\n

Given a string of digits `s`, return _the number of **palindromic subsequences** of_ `s` _having length_ `5`. Since the answer may be very large, return it **modulo** `109 + 7`. **Note:** * A string is **palindromic** if it reads the same forward and backward. * A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. **Example 1:** **Input:** s = "103301 " **Output:** 2 **Explanation:** There are 6 possible subsequences of length 5: "10330 ", "10331 ", "10301 ", "10301 ", "13301 ", "03301 ". Two of them (both equal to "10301 ") are palindromic. **Example 2:** **Input:** s = "0000000 " **Output:** 21 **Explanation:** All 21 subsequences are "00000 ", which is palindromic. **Example 3:** **Input:** s = "9999900000 " **Output:** 2 **Explanation:** The only two palindromic subsequences are "99999 " and "00000 ". **Constraints:** * `1 <= s.length <= 104` * `s` consists of digits.

Python3 Solution with dp

count-palindromic-subsequences

\n\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countPalindromes(self, s: str) -> int:\n res=0\n for i in range(10):\n for j in range(10):\n pattern=str(i)+str(j)+"|"+str(j)+str(i)\n dp=[0]*6\n dp[-1]=1\n for x in range(len(s)):\n for y in range(5):\n if s[x]==pattern[y] or y==2:\n dp[y]+=dp[y+1]\n\n res=(res+dp[0])%(10**9+7)\n\n return res \n```

Given a string of digits `s`, return _the number of **palindromic subsequences** of_ `s` _having length_ `5`. Since the answer may be very large, return it **modulo** `109 + 7`. **Note:** * A string is **palindromic** if it reads the same forward and backward. * A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. **Example 1:** **Input:** s = "103301 " **Output:** 2 **Explanation:** There are 6 possible subsequences of length 5: "10330 ", "10331 ", "10301 ", "10301 ", "13301 ", "03301 ". Two of them (both equal to "10301 ") are palindromic. **Example 2:** **Input:** s = "0000000 " **Output:** 21 **Explanation:** All 21 subsequences are "00000 ", which is palindromic. **Example 3:** **Input:** s = "9999900000 " **Output:** 2 **Explanation:** The only two palindromic subsequences are "99999 " and "00000 ". **Constraints:** * `1 <= s.length <= 104` * `s` consists of digits.

Python

count-palindromic-subsequences

# Intuition\nGo through each bigram "ab", where a and b are digits. For bigram "ab" and for each position in string s, count how many subsequences of form "ab" there are to the left of position and how many subsequences of form "ba" there are to the right. Multiplying them will give the number of palindromes of form "ab?ba" centered at given position. Sum them all up and that will be the answer.\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\ndef count(s, first_digit, second_digit):\n counts = [0, 0]\n first_digit_counts = 0\n for c in s:\n counts.append(counts[-1])\n if c == second_digit:\n counts[-1] += first_digit_counts\n if c == first_digit:\n first_digit_counts += 1\n\n return counts\n\nclass Solution:\n def countPalindromes(self, s: str) -> int:\n answer = 0\n for a in map(str, range(10)):\n for b in map(str, range(10)):\n # Count palindromes of form "ab?ba"\n counts = count(s, a, b)\n reverse_counts = count(reversed(s), a, b)\n for i, j in zip(counts, reversed(reverse_counts)):\n answer += i * j\n\n return answer % 1_000_000_007\n\n```

Given a string of digits `s`, return _the number of **palindromic subsequences** of_ `s` _having length_ `5`. Since the answer may be very large, return it **modulo** `109 + 7`. **Note:** * A string is **palindromic** if it reads the same forward and backward. * A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. **Example 1:** **Input:** s = "103301 " **Output:** 2 **Explanation:** There are 6 possible subsequences of length 5: "10330 ", "10331 ", "10301 ", "10301 ", "13301 ", "03301 ". Two of them (both equal to "10301 ") are palindromic. **Example 2:** **Input:** s = "0000000 " **Output:** 21 **Explanation:** All 21 subsequences are "00000 ", which is palindromic. **Example 3:** **Input:** s = "9999900000 " **Output:** 2 **Explanation:** The only two palindromic subsequences are "99999 " and "00000 ". **Constraints:** * `1 <= s.length <= 104` * `s` consists of digits.

Counter - O(N)

count-palindromic-subsequences

# Intuition\nFor every index `i` we find `(a, b)` in `A[:i]` and `(b, a)` in `A[i + 1:]` for all `(a, b)` in `{10} X {10}`, adding `count(a, b) * count(b, a)` to the total `R`.\n\nMore formally:\n$\\sum_{i=0}^{n - 1} \\space\\space|\\{(a, b) \\in A_{[0..i - 1]}\\}| * |\\{(b, c) \\in A_{[i + 1..n - 1]}\\}| \\space\\space\\forall\\space\\space (a, b) \\in \\{[0..9] \\times[0..9]\\}$\n\n# Complexity\nTime complexity: $\\Theta(10 \\times 10 \\times n) \\approx \\Theta(n)$\n\nSpace complexity: $\\Theta(10 + 10 + 100) \\approx \\Theta(1)$\n\n# Code\n```python\nclass Solution:\n def countPalindromes(self, A: str) -> int:\n PL = [[0 for _ in range(10)] for _ in range(10)] # f(a, b) -> count((a, b))\n PR = [[0 for _ in range(10)] for _ in range(10)] # f(a, b) -> count((a, b))\n CL = [0 for _ in range(10)] # f(a) -> count(a)\n CR = [0 for _ in range(10)] # f(a) -> count(a)\n for a in reversed(A): \n a = int(a) # increase the PR count: PR[3][3] += CR[3], PR[3][0] += CR[0], ...\n for b in range(10): # i \n PR[a][b] += CR[b] # [1,0,3,3,0,1] -> (3, 3), -> (3, 0), -> (3, 1)\n CR[a] += 1\n \n R = 0\n for a in A:\n a = int(a)\n CR[a] -= 1\n for b in range(10): # decrease PR for every lost pair\n PR[a][b] -= CR[b]\n \n for b in range(10):\n for c in range(10):\n R = (R + PL[c][b] * PR[b][c]) % (int(1e9) + 7)\n\n for b in range(10):\n PL[b][a] += CL[b]\n CL[a] += 1\n return R\n\n \n```

Given a string of digits `s`, return _the number of **palindromic subsequences** of_ `s` _having length_ `5`. Since the answer may be very large, return it **modulo** `109 + 7`. **Note:** * A string is **palindromic** if it reads the same forward and backward. * A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. **Example 1:** **Input:** s = "103301 " **Output:** 2 **Explanation:** There are 6 possible subsequences of length 5: "10330 ", "10331 ", "10301 ", "10301 ", "13301 ", "03301 ". Two of them (both equal to "10301 ") are palindromic. **Example 2:** **Input:** s = "0000000 " **Output:** 21 **Explanation:** All 21 subsequences are "00000 ", which is palindromic. **Example 3:** **Input:** s = "9999900000 " **Output:** 2 **Explanation:** The only two palindromic subsequences are "99999 " and "00000 ". **Constraints:** * `1 <= s.length <= 104` * `s` consists of digits.

O(10N) 99.5%

count-palindromic-subsequences

# Intuition\nWe can treat each digit in s as the middle and find the number of xy (middle) yx pairs that exist - then sum the total.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countPalindromes(self, s: str) -> int:\n s = [int(n) for n in s]\n r1 = [0] * 10\n r2 = [0] * 100\n for n in s[::-1]:\n for i,cnt in enumerate(r1):\n r2[n*10+i] += cnt\n r1[n] += 1\n \n l1,l2 = [0] * 10,[0] * 100\n ans, d = 0, 0\n for n in s:\n r1[n] -= 1\n for i,cnt in enumerate(r1):\n d -= l2[n*10+i] * cnt\n r2[n*10+i] -= cnt\n \n ans += d\n\n for i,cnt in enumerate(l1):\n d += r2[n*10+i] * cnt\n l2[n*10+i] += cnt\n l1[n] += 1\n \n return ans % (10 ** 9 + 7)\n\n\n \n\n\n\n\n\n \n \n\n```

Given a string of digits `s`, return _the number of **palindromic subsequences** of_ `s` _having length_ `5`. Since the answer may be very large, return it **modulo** `109 + 7`. **Note:** * A string is **palindromic** if it reads the same forward and backward. * A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. **Example 1:** **Input:** s = "103301 " **Output:** 2 **Explanation:** There are 6 possible subsequences of length 5: "10330 ", "10331 ", "10301 ", "10301 ", "13301 ", "03301 ". Two of them (both equal to "10301 ") are palindromic. **Example 2:** **Input:** s = "0000000 " **Output:** 21 **Explanation:** All 21 subsequences are "00000 ", which is palindromic. **Example 3:** **Input:** s = "9999900000 " **Output:** 2 **Explanation:** The only two palindromic subsequences are "99999 " and "00000 ". **Constraints:** * `1 <= s.length <= 104` * `s` consists of digits.

Very naive O(n) solution.

count-palindromic-subsequences

# Intuition\nThe intuition: we keep open a set of machines which look hungrily for letters. Starting out the machines have no state and will accept any letter, once they accept one letter char they take on a partial state (0, char), and will accept any letter. The next time they encounter a letter char\' they transition to state (1, (char, char\')) and will again accept any letter. Upon the third letter of any type they transition to state (3, (char, char\')) and will only accept only char\'. And so on. Once they have consumed an entire palindrome 1 is added to the count. \n\nKeeping some kind of class structure or array for all of these machines is costly in space and costly to update in time, but because our vocabulary of letters is just [0-9] it is relatively cheap to just keep a dictionary of the number of machines in each state, which is what we do with the dictionary d.\n\n# Approach\nPretty much exactly the same as the intuition section. The dictionary d[i][k] keeps track of the number of machines in state (i, k) in the above discussion. \n\n# Complexity\n- Time complexity:\nThere are a maximum of 10 keys for d[0], 10^2 for d[1], d[2]. So a maximum of 312 or so operations are performed for each character (including the if statement). The complexity is thus O(n).\n\n- Space complexity:\nO(1), the only significant space is taken up by the dictionary. \n\n# Code\n```\nfrom collections import defaultdict\nclass Solution:\n def countPalindromes(self, s: str) -> int:\n p = (10**9) + 7\n count = 0\n d = [defaultdict(lambda:0) for j in range(4)]\n for ind, i in enumerate(s):\n count += d[3][i]\n for l in d[2].keys():\n if l[1] == i:\n d[3][l[0]] += d[2][l]\n for k in d[1].keys():\n d[2][k] += d[1][k]\n for j in d[0].keys():\n d[1][(j,i)] += d[0][j]\n d[0][i] += 1\n return (count % p)\n \n```

Given a string of digits `s`, return _the number of **palindromic subsequences** of_ `s` _having length_ `5`. Since the answer may be very large, return it **modulo** `109 + 7`. **Note:** * A string is **palindromic** if it reads the same forward and backward. * A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. **Example 1:** **Input:** s = "103301 " **Output:** 2 **Explanation:** There are 6 possible subsequences of length 5: "10330 ", "10331 ", "10301 ", "10301 ", "13301 ", "03301 ". Two of them (both equal to "10301 ") are palindromic. **Example 2:** **Input:** s = "0000000 " **Output:** 21 **Explanation:** All 21 subsequences are "00000 ", which is palindromic. **Example 3:** **Input:** s = "9999900000 " **Output:** 2 **Explanation:** The only two palindromic subsequences are "99999 " and "00000 ". **Constraints:** * `1 <= s.length <= 104` * `s` consists of digits.

Faster than 100%. Python implementation using numpy.

count-palindromic-subsequences

# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe implement the prefix/suffix solution in numpy.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nWe build a running "bag" of characters:\n- `bag.singles` -- `bag.singles[n]` is the number of times n appears in the list\n- `bag.duples` -- An array of shape (10,10) where `bag.duples[n, m]` counts the number of subsequences n, m.\n- `bag.append(n)` -- Add a character to the end of the list. Adjust singles and duples accordingly.\n- `bag.pop0(n)` -- Remove a character from the beginning of the list. Adjust singles and duples accordingly.\n\nWe will have a `before_bag` and an `after_bag` to describe the list of characters before and after the current character.\n\n#### Finding the number of palindromes centered on the current character is a one-liner!\n- `(after_bag.duples * before_bag.duples.T).sum()`\n\n# Complexity\n- Time complexity: O(100n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(100)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport numpy as np\n\nclass Solution:\n def countPalindromes(self, s: str) -> int:\n after_bag, before_bag = Bag(), Bag()\n for c in s:\n after_bag.append(int(c))\n cnt = 0\n for c in s:\n n = int(c)\n after_bag.pop0(n)\n cnt += (after_bag.duples * before_bag.duples.T).sum()\n before_bag.append(n)\n cnt = int(cnt) % (10**9 + 7)\n return cnt\n\nclass Bag:\n def __init__(self):\n self.singles = np.zeros(10)\n self.duples = np.zeros((10,10))\n\n def append(self, n):\n self.duples[:, n] += self.singles\n self.singles[n] += 1\n\n def pop0(self, n):\n self.singles[n] -= 1\n self.duples[n, :] -= self.singles\n\n\n\n\n\n```

Given a string of digits `s`, return _the number of **palindromic subsequences** of_ `s` _having length_ `5`. Since the answer may be very large, return it **modulo** `109 + 7`. **Note:** * A string is **palindromic** if it reads the same forward and backward. * A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. **Example 1:** **Input:** s = "103301 " **Output:** 2 **Explanation:** There are 6 possible subsequences of length 5: "10330 ", "10331 ", "10301 ", "10301 ", "13301 ", "03301 ". Two of them (both equal to "10301 ") are palindromic. **Example 2:** **Input:** s = "0000000 " **Output:** 21 **Explanation:** All 21 subsequences are "00000 ", which is palindromic. **Example 3:** **Input:** s = "9999900000 " **Output:** 2 **Explanation:** The only two palindromic subsequences are "99999 " and "00000 ". **Constraints:** * `1 <= s.length <= 104` * `s` consists of digits.

🔥🔥PYTHON🔥🔥 Very Easy 4 liner

find-the-pivot-integer

\n# Code\n```\nclass Solution:\n def pivotInteger(self, n: int) -> int:\n s1 = 0\n s2 = 0\n for i in range(1,n+1):\n s1 = sum(range(1, i+1))\n s2 = sum(range(i, n+1))\n if(s1==s2):\n return i\n return -1\n\n```

Given a positive integer `n`, find the **pivot integer** `x` such that: * The sum of all elements between `1` and `x` inclusively equals the sum of all elements between `x` and `n` inclusively. Return _the pivot integer_ `x`. If no such integer exists, return `-1`. It is guaranteed that there will be at most one pivot index for the given input. **Example 1:** **Input:** n = 8 **Output:** 6 **Explanation:** 6 is the pivot integer since: 1 + 2 + 3 + 4 + 5 + 6 = 6 + 7 + 8 = 21. **Example 2:** **Input:** n = 1 **Output:** 1 **Explanation:** 1 is the pivot integer since: 1 = 1. **Example 3:** **Input:** n = 4 **Output:** -1 **Explanation:** It can be proved that no such integer exist. **Constraints:** * `1 <= n <= 1000`

Solution of find the pivot integer problem

find-the-pivot-integer

# Approach\n### Solved using algebraic progression\n- The sum of the members of a finite arithmetic progression is called an arithmetic series.\n- This sum can be found quickly by taking the number n of terms being added, multiplying by the sum of the first and last number in the progressio and dividing by 2\n- In this problem we have two algebraic progressions:\n1. from 1 to pivot --> $$(1 + pivot) * pivot / 2$$\n2. from pivot to n --> $$(pivot + n) * (n - pivot + 1) / 2$$\n- If they are equal to each other: `return pivot`\n- Else: `return -1`\n\n# Complexity\n- Time complexity:\n$$O(n)$$ - as loop takes linear time\n\n- Space complexity:\n$$O(1)$$ - as, no extra space is required.\n\n# Code\n```\nclass Solution:\n def pivotInteger(self, n: int) -> int:\n for pivot in range(1, n + 1):\n if (1 + pivot) * pivot == (pivot + n) * (n - pivot + 1):\n return pivot\n return -1\n```

Given a positive integer `n`, find the **pivot integer** `x` such that: * The sum of all elements between `1` and `x` inclusively equals the sum of all elements between `x` and `n` inclusively. Return _the pivot integer_ `x`. If no such integer exists, return `-1`. It is guaranteed that there will be at most one pivot index for the given input. **Example 1:** **Input:** n = 8 **Output:** 6 **Explanation:** 6 is the pivot integer since: 1 + 2 + 3 + 4 + 5 + 6 = 6 + 7 + 8 = 21. **Example 2:** **Input:** n = 1 **Output:** 1 **Explanation:** 1 is the pivot integer since: 1 = 1. **Example 3:** **Input:** n = 4 **Output:** -1 **Explanation:** It can be proved that no such integer exist. **Constraints:** * `1 <= n <= 1000`

[C++|Java|Python3] pointer

append-characters-to-string-to-make-subsequence

Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/e728a9f475e5742bea7cf67ac2d1a98ab99fb206) for solutions of weekly 321. \n\n**Intuition**\nHere, we can simply check if the characters of t are sequentially present in s. If not, the length of remaining characters in t is the answer. \n**Implementation\n**C++**\n```\nclass Solution {\npublic:\n int appendCharacters(string s, string t) {\n int i = 0; \n for (auto& ch : s) \n if (i < t.size() && ch == t[i]) ++i; \n return t.size() - i; \n }\n};\n```\n**Java**\n```\nclass Solution {\n public int appendCharacters(String s, String t) {\n int i = 0; \n for (char ch : s.toCharArray()) \n if (i < t.length() && ch == t.charAt(i)) ++i; \n return t.length()-i; \n }\n}\n```\n**Python3**\n```\t\t\nclass Solution:\n def appendCharacters(self, s: str, t: str) -> int:\n it = iter(s)\n return next((len(t)-i for i, ch in enumerate(t) if ch not in it), 0)\n```\t\t\n**Complexity**\nTime O(N)\nSpace O(1)

You are given two strings `s` and `t` consisting of only lowercase English letters. Return _the minimum number of characters that need to be appended to the end of_ `s` _so that_ `t` _becomes a **subsequence** of_ `s`. A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. **Example 1:** **Input:** s = "coaching ", t = "coding " **Output:** 4 **Explanation:** Append the characters "ding " to the end of s so that s = "coachingding ". Now, t is a subsequence of s ( "**co**aching**ding** "). It can be shown that appending any 3 characters to the end of s will never make t a subsequence. **Example 2:** **Input:** s = "abcde ", t = "a " **Output:** 0 **Explanation:** t is already a subsequence of s ( "**a**bcde "). **Example 3:** **Input:** s = "z ", t = "abcde " **Output:** 5 **Explanation:** Append the characters "abcde " to the end of s so that s = "zabcde ". Now, t is a subsequence of s ( "z**abcde** "). It can be shown that appending any 4 characters to the end of s will never make t a subsequence. **Constraints:** * `1 <= s.length, t.length <= 105` * `s` and `t` consist only of lowercase English letters.

Easy solution in python

append-characters-to-string-to-make-subsequence

class Solution:\n def appendCharacters(self, s: str, t: str) -> int:\n t=list(t)\n for i in s:\n if len(t)==0:\n return 0\n if(i==t[0]):\n t.pop(0)\n return len(t)\n```

You are given two strings `s` and `t` consisting of only lowercase English letters. Return _the minimum number of characters that need to be appended to the end of_ `s` _so that_ `t` _becomes a **subsequence** of_ `s`. A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. **Example 1:** **Input:** s = "coaching ", t = "coding " **Output:** 4 **Explanation:** Append the characters "ding " to the end of s so that s = "coachingding ". Now, t is a subsequence of s ( "**co**aching**ding** "). It can be shown that appending any 3 characters to the end of s will never make t a subsequence. **Example 2:** **Input:** s = "abcde ", t = "a " **Output:** 0 **Explanation:** t is already a subsequence of s ( "**a**bcde "). **Example 3:** **Input:** s = "z ", t = "abcde " **Output:** 5 **Explanation:** Append the characters "abcde " to the end of s so that s = "zabcde ". Now, t is a subsequence of s ( "z**abcde** "). It can be shown that appending any 4 characters to the end of s will never make t a subsequence. **Constraints:** * `1 <= s.length, t.length <= 105` * `s` and `t` consist only of lowercase English letters.

Python | Clean Code | O(n) Time and O(1) Space |

append-characters-to-string-to-make-subsequence

# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def appendCharacters(self, s: str, t: str) -> int:\n count = 0\n j = 0\n for i in s:\n if j == len(t):\n return 0\n if i == t[j]:\n j += 1\n count += 1\n return len(t) - count\n```

You are given two strings `s` and `t` consisting of only lowercase English letters. Return _the minimum number of characters that need to be appended to the end of_ `s` _so that_ `t` _becomes a **subsequence** of_ `s`. A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. **Example 1:** **Input:** s = "coaching ", t = "coding " **Output:** 4 **Explanation:** Append the characters "ding " to the end of s so that s = "coachingding ". Now, t is a subsequence of s ( "**co**aching**ding** "). It can be shown that appending any 3 characters to the end of s will never make t a subsequence. **Example 2:** **Input:** s = "abcde ", t = "a " **Output:** 0 **Explanation:** t is already a subsequence of s ( "**a**bcde "). **Example 3:** **Input:** s = "z ", t = "abcde " **Output:** 5 **Explanation:** Append the characters "abcde " to the end of s so that s = "zabcde ". Now, t is a subsequence of s ( "z**abcde** "). It can be shown that appending any 4 characters to the end of s will never make t a subsequence. **Constraints:** * `1 <= s.length, t.length <= 105` * `s` and `t` consist only of lowercase English letters.

[Python3] Greedy Five Lines

append-characters-to-string-to-make-subsequence

**Weekly Contest 321 Submission**\n\n**Greedy Five Lines**\n\n**Algorithm**\n1. Find the largest *subsequence* initial fragment of `t` from `s`. This can be done greedily by consistently popping the front character of `t` when iterating `s` if `c` == `t[0]`.\n2. If all characters of `t` are popped during the iteration of `s` then `t` is already a *subsequence* of `s` (no needed additions - return 0).\n3. The left over characters of `t` (those not in the largest *subsequence* initial fragment) must be appended to `s` (return the length of the resulting `t` after iterating `s`).\n\n**Code**\n```Python3 []\nclass Solution:\n def appendCharacters(self, s: str, t: str) -> int:\n #Reversed in order to pop the first character each time\n t = list(t)[::-1]\n \n for c in s:\n #t is already a subsequence\n if not t: return 0\n #pop t if c == "first character" of t \n if c == t[-1]: t.pop()\n \n #Return the left over t length\n return len(t) \n```\n

You are given two strings `s` and `t` consisting of only lowercase English letters. Return _the minimum number of characters that need to be appended to the end of_ `s` _so that_ `t` _becomes a **subsequence** of_ `s`. A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. **Example 1:** **Input:** s = "coaching ", t = "coding " **Output:** 4 **Explanation:** Append the characters "ding " to the end of s so that s = "coachingding ". Now, t is a subsequence of s ( "**co**aching**ding** "). It can be shown that appending any 3 characters to the end of s will never make t a subsequence. **Example 2:** **Input:** s = "abcde ", t = "a " **Output:** 0 **Explanation:** t is already a subsequence of s ( "**a**bcde "). **Example 3:** **Input:** s = "z ", t = "abcde " **Output:** 5 **Explanation:** Append the characters "abcde " to the end of s so that s = "zabcde ". Now, t is a subsequence of s ( "z**abcde** "). It can be shown that appending any 4 characters to the end of s will never make t a subsequence. **Constraints:** * `1 <= s.length, t.length <= 105` * `s` and `t` consist only of lowercase English letters.

[Java/Python 3] Two pointers O(n) codes w/ brief explanation and analysis.

append-characters-to-string-to-make-subsequence

\n1. Traverse `s`, if current char is same as current char of `t`, increase by 1 the pointer for `t`, `idx`.\n2. Deducting the size of `t` by `idx` is the answer.\n\n```java\n public int appendCharacters(String s, String t) {\n int idx = 0;\n for (int i = 0; i < s.length(); ++i) {\n if (idx < t.length() && s.charAt(i) == t.charAt(idx)) {\n ++idx;\n }\n }\n return t.length() - idx;\n }\n```\n```python\n def appendCharacters(self, s: str, t: str) -> int:\n idx, n = 0, len(t)\n for c in s:\n if idx < n and t[idx] == c:\n idx += 1\n return n - idx\n```\n\n**Analysis:**\n\nTime: `O(n)`, space: `O(1)`

You are given two strings `s` and `t` consisting of only lowercase English letters. Return _the minimum number of characters that need to be appended to the end of_ `s` _so that_ `t` _becomes a **subsequence** of_ `s`. A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. **Example 1:** **Input:** s = "coaching ", t = "coding " **Output:** 4 **Explanation:** Append the characters "ding " to the end of s so that s = "coachingding ". Now, t is a subsequence of s ( "**co**aching**ding** "). It can be shown that appending any 3 characters to the end of s will never make t a subsequence. **Example 2:** **Input:** s = "abcde ", t = "a " **Output:** 0 **Explanation:** t is already a subsequence of s ( "**a**bcde "). **Example 3:** **Input:** s = "z ", t = "abcde " **Output:** 5 **Explanation:** Append the characters "abcde " to the end of s so that s = "zabcde ". Now, t is a subsequence of s ( "z**abcde** "). It can be shown that appending any 4 characters to the end of s will never make t a subsequence. **Constraints:** * `1 <= s.length, t.length <= 105` * `s` and `t` consist only of lowercase English letters.

Simple , compact and Recursive.

remove-nodes-from-linked-list

# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def removeNodes(self, head: Optional[ListNode]) -> Optional[ListNode]:\n def removeNode (head):\n if (head == None):\n return None\n head.next = removeNode(head.next);\n return head.next if (head.next != None and head.val < head.next.val) else head;\n return removeNode(head) \n```

You are given the `head` of a linked list. Remove every node which has a node with a **strictly greater** value anywhere to the right side of it. Return _the_ `head` _of the modified linked list._ **Example 1:** **Input:** head = \[5,2,13,3,8\] **Output:** \[13,8\] **Explanation:** The nodes that should be removed are 5, 2 and 3. - Node 13 is to the right of node 5. - Node 13 is to the right of node 2. - Node 8 is to the right of node 3. **Example 2:** **Input:** head = \[1,1,1,1\] **Output:** \[1,1,1,1\] **Explanation:** Every node has value 1, so no nodes are removed. **Constraints:** * The number of the nodes in the given list is in the range `[1, 105]`. * `1 <= Node.val <= 105`

[Java/Python 3] 3 codes: Recursive, Iterative space O(n) and extra space O(1).

remove-nodes-from-linked-list

**Method 1: Recursive**\n\nDuring recursion to the end of the list, check if the value of current node less than that of the next one; If yes, return next node and ignore current one.\n\n```java\n public ListNode removeNodes(ListNode head) {\n if (head != null) {\n head.next = removeNodes(head.next);\n if (head.next != null && head.val < head.next.val) {\n return head.next;\n }\n }\n return head;\n }\n```\n```python\n def removeNodes(self, head: Optional[ListNode]) -> Optional[ListNode]:\n if head:\n head.next = self.removeNodes(head.next)\n if head.next and head.val < head.next.val:\n return head.next\n return head\n```\n**Analysis:**\n\nTime & space: `O(n)`, where `n` is the # of nodes.\n\n\n----\n\n**Method 2: non-increasing Stack**\n\n1. Keep popping out the stack top node that is smaller than current one.\n2. Connect all nodes remaining in the stack and return the stack bottom node.\n\n```java\n public ListNode removeNodes(ListNode head) {\n Deque<ListNode> stk = new ArrayDeque<>();\n while (head != null) {\n while (!stk.isEmpty() && stk.peek().val < head.val) {\n stk.pop();\n }\n stk.push(head);\n head = head.next;\n }\n while (stk.size() > 1) {\n ListNode n = stk.pop();\n stk.peek().next = n;\n }\n return stk.peek();\n }\n```\n```python\n def removeNodes(self, head: Optional[ListNode]) -> Optional[ListNode]:\n stk = []\n while head:\n while stk and stk[-1].val < head.val:\n stk.pop()\n stk.append(head)\n head = head.next\n while len(stk) > 1:\n node = stk.pop()\n stk[-1].next = node\n return stk[-1]\n```\n\n**Analysis:**\n\nTime & space: `O(n)`, where `n` is the # of nodes.\n\n----\n\n**Method 3: Extra space O(1), reverse and remove decreasing nodes.**\n\n\n1. Reverse the list;\n2. Traverse the list and compute the running maximum, remove any decreasing nodes.\n3. Reverse the list once again to resore the order.\n\n```java\n public ListNode removeNodes(ListNode head) {\n ListNode tail = reverse(head), cur = tail;\n int mx = cur.val;\n while (cur.next != null) {\n if (cur.next.val < mx) {\n cur.next = cur.next.next;\n }else {\n cur = cur.next;\n mx = cur.val;\n }\n }\n return reverse(tail);\n }\n private ListNode reverse(ListNode n) {\n ListNode tail = null;\n while (n != null) {\n ListNode next = n.next;\n n.next = tail;\n tail = n;\n n = next;\n }\n return tail;\n }\n```\n```python\n def removeNodes(self, head: Optional[ListNode]) -> Optional[ListNode]:\n \n def reverse(n: ListNode) -> ListNode:\n tail = None\n while n:\n nxt = n.next\n n.next = tail\n tail = n\n n = nxt\n return tail\n\n cur = tail = reverse(head)\n mx = cur.val\n while cur.next:\n if cur.next.val < mx:\n cur.next = cur.next.next\n else:\n cur = cur.next\n mx = cur.val\n return reverse(tail)\n```\n\n**Analysis:**\n\nHaving used the given input list, strictly speaking, the space cost is the whole given list `O(n)`, or `O(1)` extra space.\n\nTime: `O(n)`, extra space: `O(1)`, where `n` is the # of nodes.

You are given the `head` of a linked list. Remove every node which has a node with a **strictly greater** value anywhere to the right side of it. Return _the_ `head` _of the modified linked list._ **Example 1:** **Input:** head = \[5,2,13,3,8\] **Output:** \[13,8\] **Explanation:** The nodes that should be removed are 5, 2 and 3. - Node 13 is to the right of node 5. - Node 13 is to the right of node 2. - Node 8 is to the right of node 3. **Example 2:** **Input:** head = \[1,1,1,1\] **Output:** \[1,1,1,1\] **Explanation:** Every node has value 1, so no nodes are removed. **Constraints:** * The number of the nodes in the given list is in the range `[1, 105]`. * `1 <= Node.val <= 105`

Python || Recursive Code || Beats 90% Time Complexity 🔥

remove-nodes-from-linked-list

# Code\n```\nclass Solution:\n def removeNodes(self, head: Optional[ListNode]) -> Optional[ListNode]:\n if head is None:\n return None\n head.next = self.removeNodes(head.next)\n if head.next and head.val < head.next.val:\n return head.next\n return head\n```

You are given the `head` of a linked list. Remove every node which has a node with a **strictly greater** value anywhere to the right side of it. Return _the_ `head` _of the modified linked list._ **Example 1:** **Input:** head = \[5,2,13,3,8\] **Output:** \[13,8\] **Explanation:** The nodes that should be removed are 5, 2 and 3. - Node 13 is to the right of node 5. - Node 13 is to the right of node 2. - Node 8 is to the right of node 3. **Example 2:** **Input:** head = \[1,1,1,1\] **Output:** \[1,1,1,1\] **Explanation:** Every node has value 1, so no nodes are removed. **Constraints:** * The number of the nodes in the given list is in the range `[1, 105]`. * `1 <= Node.val <= 105`

Python | Easy Solution | Linked List | Arrays

remove-nodes-from-linked-list

# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def removeNodes(self, head: Optional[ListNode]) -> Optional[ListNode]:\n arr = []\n currMax = -99999\n while head:\n # print(arr)\n if len(arr) == 0:\n currMax = head.val\n arr.append(head.val)\n else:\n if head.val > currMax:\n currMax = head.val\n arr = [head.val]\n \n else:\n if head.val > arr[-1]:\n for i in range(len(arr)-1, -1, -1):\n if head.val > arr[i]:\n arr.pop()\n else:\n break\n arr.append(head.val)\n head = head.next\n # print(arr)\n d = n = ListNode()\n for i in arr:\n n.next = ListNode(i)\n n = n.next\n return d.next\n\n\n```

You are given the `head` of a linked list. Remove every node which has a node with a **strictly greater** value anywhere to the right side of it. Return _the_ `head` _of the modified linked list._ **Example 1:** **Input:** head = \[5,2,13,3,8\] **Output:** \[13,8\] **Explanation:** The nodes that should be removed are 5, 2 and 3. - Node 13 is to the right of node 5. - Node 13 is to the right of node 2. - Node 8 is to the right of node 3. **Example 2:** **Input:** head = \[1,1,1,1\] **Output:** \[1,1,1,1\] **Explanation:** Every node has value 1, so no nodes are removed. **Constraints:** * The number of the nodes in the given list is in the range `[1, 105]`. * `1 <= Node.val <= 105`

Simple. Reverse the list. Tack local max.

remove-nodes-from-linked-list

# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIterate in the reversed order. Track local maximum value.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Reverse the list.\n2. Iterate through the list tracking max value;\n a. If a current value less that the local max value Remove the node;\n b. Keep iterating.\n5. Return the list.\n# Complexity\n- Time complexity:$$O(2*n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python []\nclass Solution:\n def reverse_list(self, head):\n prev, current = None, head\n\n while current:\n next_node = current.next\n current.next = prev\n prev = current\n current = next_node\n \n head = prev\n \n return head\n\n def removeNodes(self, head: Optional[ListNode]) -> Optional[ListNode]:\n head = self.reverse_list(head)\n\n local_max = 0\n prev, current = None, head\n\n while current:\n local_max = max(local_max, current.val)\n\n if current.val < local_max:\n if prev:\n prev.next = current.next\n else:\n head = current.next\n current = current.next\n else:\n prev, current = current, current.next\n \n return self.reverse_list(head)\n```\n```javascript []\nvar removeNodes = function(head) {\n head = reverseList(head);\n\n let prev = null;\n let curr = head;\n let local_max = 0;\n\n while (curr !== null) {\n local_max = Math.max(local_max, curr.val);\n\n if (curr.val < local_max) {\n if (prev !== null) {\n prev.next = curr.next\n } else {\n head = curr.next\n };\n curr = curr.next;\n } else {\n prev = curr;\n curr = curr.next;\n };\n };\n\n return reverseList(head);\n};\n\nconst reverseList = (head) => {\n let prev = null;\n let curr = head;\n\n while (curr !== null) {\n let next_node = curr.next\n curr.next = prev;\n prev = curr;\n curr = next_node;\n };\n head = prev;\n return head;\n};\n```\n# ***Please UPVOTE !!!***\n\n---\n\n

You are given the `head` of a linked list. Remove every node which has a node with a **strictly greater** value anywhere to the right side of it. Return _the_ `head` _of the modified linked list._ **Example 1:** **Input:** head = \[5,2,13,3,8\] **Output:** \[13,8\] **Explanation:** The nodes that should be removed are 5, 2 and 3. - Node 13 is to the right of node 5. - Node 13 is to the right of node 2. - Node 8 is to the right of node 3. **Example 2:** **Input:** head = \[1,1,1,1\] **Output:** \[1,1,1,1\] **Explanation:** Every node has value 1, so no nodes are removed. **Constraints:** * The number of the nodes in the given list is in the range `[1, 105]`. * `1 <= Node.val <= 105`

Python || prefix sum || O(n)

count-subarrays-with-median-k

First we transform `nums` into an array of -1, 0, 1: \nn < k to -1, n == k to 0, n > k to 1.\nFor example, `nums` = [5,1,3,4,2], k = 4 -> arr = [1,-1,-1,0,-1]\n\nFor a subarray with sum equals to 0, number of {n: n < k} = number of {n: n > k}.\nFor a subarray with sum equals to 1, number of {n: n < k} = number of {n: n > k} - 1.\nEvery subarray containing 0 and with sum equals to 0(odd length) or 1(even length) counts.\n\n```\nclass Solution:\n def countSubarrays(self, nums: List[int], k: int) -> int:\n arr = []\n for n in nums:\n if n < k:\n arr.append(-1)\n elif n > k:\n arr.append(1)\n else:\n arr.append(0)\n \n book_pre = Counter()\n book_pre[0] = 1\n agg = 0\n check = False\n ans = 0\n for a in arr:\n if a == 0:\n check = True\n agg += a\n if check:\n ans += book_pre[agg] + book_pre[agg-1]\n else:\n book_pre[agg] += 1\n return ans

You are given an array `nums` of size `n` consisting of **distinct** integers from `1` to `n` and a positive integer `k`. Return _the number of non-empty subarrays in_ `nums` _that have a **median** equal to_ `k`. **Note**: * The median of an array is the **middle** element after sorting the array in **ascending** order. If the array is of even length, the median is the **left** middle element. * For example, the median of `[2,3,1,4]` is `2`, and the median of `[8,4,3,5,1]` is `4`. * A subarray is a contiguous part of an array. **Example 1:** **Input:** nums = \[3,2,1,4,5\], k = 4 **Output:** 3 **Explanation:** The subarrays that have a median equal to 4 are: \[4\], \[4,5\] and \[1,4,5\]. **Example 2:** **Input:** nums = \[2,3,1\], k = 3 **Output:** 1 **Explanation:** \[3\] is the only subarray that has a median equal to 3. **Constraints:** * `n == nums.length` * `1 <= n <= 105` * `1 <= nums[i], k <= n` * The integers in `nums` are distinct.

[Python3] freq table

count-subarrays-with-median-k

Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/e728a9f475e5742bea7cf67ac2d1a98ab99fb206) for solutions of weekly 321. \n\n**Intuition**\nThe subarray whose median is `k` has to include `k` itself. So we construct our subarrays starting from where `k` is located. \nWe find the index of `k` (say `idx`). Then, we first move to the left and write down the difference of counts larger than k and smaller than `k`. \nLater, we move to the right and calculate the same difference. Here, we can calculate the number of subarrays with median equal to `k` ending at the current index via `freq[-diff]`. \n**Implementation**\n```\nclass Solution:\n def countSubarrays(self, nums: List[int], k: int) -> int:\n idx = nums.index(k)\n freq = Counter()\n prefix = 0\n for i in reversed(range(idx+1)): \n prefix += int(nums[i] > k) - int(nums[i] < k)\n freq[prefix] += 1\n ans = prefix = 0 \n for i in range(idx, len(nums)): \n prefix += int(nums[i] > k) - int(nums[i] < k)\n ans += freq[-prefix] + freq[-prefix+1]\n return ans \n```\n**Complexity**\nTime O(N)\nSpace O(N)\n\nAlternative implementation inspired by @rock\n```\nclass Solution:\n def countSubarrays(self, nums: List[int], k: int) -> int:\n freq = Counter({0 : 1})\n ans = diff = found = 0\n for x in nums: \n if x < k: diff -= 1\n elif x > k: diff += 1\n else: found = 1\n if found: ans += freq[diff] + freq[diff-1]\n else: freq[diff] += 1\n return ans \n```

You are given an array `nums` of size `n` consisting of **distinct** integers from `1` to `n` and a positive integer `k`. Return _the number of non-empty subarrays in_ `nums` _that have a **median** equal to_ `k`. **Note**: * The median of an array is the **middle** element after sorting the array in **ascending** order. If the array is of even length, the median is the **left** middle element. * For example, the median of `[2,3,1,4]` is `2`, and the median of `[8,4,3,5,1]` is `4`. * A subarray is a contiguous part of an array. **Example 1:** **Input:** nums = \[3,2,1,4,5\], k = 4 **Output:** 3 **Explanation:** The subarrays that have a median equal to 4 are: \[4\], \[4,5\] and \[1,4,5\]. **Example 2:** **Input:** nums = \[2,3,1\], k = 3 **Output:** 1 **Explanation:** \[3\] is the only subarray that has a median equal to 3. **Constraints:** * `n == nums.length` * `1 <= n <= 105` * `1 <= nums[i], k <= n` * The integers in `nums` are distinct.

✅ [Python] Multiply diff counts around median | O(n) Solution w/ Explanation

count-subarrays-with-median-k

# Intuition\n**Brute Force - O(n^3)**\nYou should always start by coming up with the brute force solution. In this case, we can check every possible subarray, count the number of elements above/below the median, and check that the median exists in the subarray. As long as there are the same number of elements above/below, or there is 1 more above than below, then the subarray is accepted.\n\n\nEx: [1,2,3,4], k=2\n[1] - no\n[1,2] - no\n[1,2,3] - yes (1 below, 1 above)\n[1,2,3,4] - yes (1 below, 2 above)\n[2] - yes\n[2,3] - yes (0 below, 1 above)\n[2,3,4] - no\n...other subarrays do not contain 3 so they would be invalid.\n\n\n---\n\n\n\n**Optimization to O(n^2)**\nSince the size of nums can be very large (up to 10^5), it\'s clear we need a solution with O(n) time. It\'s also clear that any subarray that doesn\'t contain k is useless, so our 1st potential approach could be to find where k is in nums. After that, perhaps we can use some sort of left and right pointer, expand the subarray being considered around k, and verify the total number of above elements is equal to (or 1 more greater) than the number of below elements being considered. \n\nNote: The left pointer will consider elements to the left of the median, and the right pointer for elements to the right of the median\n\n\nEx: [1,2,3,4,5], k=3\nl=1,r=3 yes\nl=1,r=4 yes\nl=0,r=3 no\nl=0,r=4 yes\n(There is also the subarray of just [3], which we can manually add to the 4 above for a total of 5)\n\n\nWhile this makes sense, this still requires us to consider every possible combination of left pointer and right pointer so that we cover all possible subarrays that contain the median. This results in O(n^2) runtime - still a little slow.\n\n\n# Approach\n**Optimization to O(n)**\nThe realization we need to make to reach O(n) time is the fact that we are going to see the same differences between above/below on the left side and right side of the median. And, we might see those same differences multiple times.\n\nExample: Let med = index of the median.\nSuppose at some l < med, we have 3 above and 1 below, then the diff is -2 total (below - above). In order to set k as the median with these 4 elements on the left (3 above/1 below) we need to know all the subarrays to the right of med which can "balance out" the missing 2 below from the left side. \n\nIf we calculate the diffs of the above/below counts for all r, where med < r < n, then we would know instantly whether there are any subarrays to the right which have a diff of 2 (ie 2 more below than above). That\'s all we need to balance out our left side.\n\nThe only hitch here is if we have a diff of -2 occurring multiple times on the left side. In that case, every one of those will need a diff of 2 on the right side. And if there were multiple diffs of 2 occurring on the right side, then every one those is a valid r to pick for completing the subarray. To handle this, we can do a standard multiplication to add all possible combinations of left side and right matching diffs.\n\nNote: To accommodate the fact that even arrays need 1 more above than below, we also multiply by -diff - 1 on the right side, which represents the diffs that would have one extra above to add to our total subarray.\n\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n\n- `diff` represents the difference between the number of above/below elements (ie below - above)\n- We initialize `res` with the left/right diffs of 0 since that represents subarrays that use elements only on the left/right side of the median. (Likewise for -1, where we have one extra above than below only on one side.)\n\n```\nclass Solution:\n def countSubarrays(self, nums: List[int], k: int) -> int:\n n = len(nums)\n med_i = nums.index(k)\n\n left_of_med_diff_counts = collections.defaultdict(int)\n diff = 0\n for l in range(med_i - 1, -1, -1):\n diff += 1 if nums[l] < k else -1\n left_of_med_diff_counts[diff] += 1\n\n right_of_med_diff_counts = collections.defaultdict(int)\n diff = 0\n for r in range(med_i + 1, n):\n diff += 1 if nums[r] < k else -1\n right_of_med_diff_counts[diff] += 1\n\n res = left_of_med_diff_counts[0] + right_of_med_diff_counts[0] \\\n + left_of_med_diff_counts[-1] + right_of_med_diff_counts[-1] + 1\n for diff, total in left_of_med_diff_counts.items():\n res += (total * right_of_med_diff_counts[-diff]) + (total * right_of_med_diff_counts[-diff - 1])\n return res\n```\n\nI hope that was helpful! (Please upvote if so)

You are given an array `nums` of size `n` consisting of **distinct** integers from `1` to `n` and a positive integer `k`. Return _the number of non-empty subarrays in_ `nums` _that have a **median** equal to_ `k`. **Note**: * The median of an array is the **middle** element after sorting the array in **ascending** order. If the array is of even length, the median is the **left** middle element. * For example, the median of `[2,3,1,4]` is `2`, and the median of `[8,4,3,5,1]` is `4`. * A subarray is a contiguous part of an array. **Example 1:** **Input:** nums = \[3,2,1,4,5\], k = 4 **Output:** 3 **Explanation:** The subarrays that have a median equal to 4 are: \[4\], \[4,5\] and \[1,4,5\]. **Example 2:** **Input:** nums = \[2,3,1\], k = 3 **Output:** 1 **Explanation:** \[3\] is the only subarray that has a median equal to 3. **Constraints:** * `n == nums.length` * `1 <= n <= 105` * `1 <= nums[i], k <= n` * The integers in `nums` are distinct.

[Java/Python 3/C++] 1 pass O(n) codes: Count the prefix sum of the balance of (greater - samller).

count-subarrays-with-median-k

**Key observation:** Within any subarray, the # of elements greater than median - the # of those less than median `= 0` or `1`.\n\nIn order to guarantee the median `k` to present in subarrays, we ONLY save into HashMap/dict the frequencies of the running balances BEFORE finding the median `k`. e.g., \n\n`nums = [7, 1, 3, 4, 2, 5, 6], k = 4`\nrunning balance:\n`bals = [1, 0,-1,-1,-2,-1, 0]`\nAt index:\n-1: running balance = 0 Note: -1 is a vertual index for dummy value 0. \n0: running balance = 1\n1: running balance = 0\n2: running balance = -1\n3: running balance = -1, median k found! stop saving the frequencies into HashMap/dict.\n4: running balance = -2, begin to count the # of subarrays but no subarray meet the requirement yet. \n5: running balance = -1, there are `2` `-1`s at index `2` & `3`, respectively. The corresponding subarrays are from index `3` to `5` and `4` to `5`: `[4,2,5]` & `[4,5]`. Note: though `(-1 -1) == -2` at index `4`, it is not what we need, because the subarray from index `5` to index `5`, `[5]`, does not include median at index `3`.\n6: running balance = 0, there are a `0` at index `1` and dummy value of `0` at index `-1`: `[3,4,2,5,6]` & `[7,1,3,4,2,5,6]`, and two `0 - 1 == -1`s at index `2` & `3`: `[3,4,2,5,6]` & `[4,2,5,6]`.\n\n\nWe have to use the running balance after median to minus the running balance before the median. Otherwise, we could NOT make sure the median is in the subarray.\n\n----\n\nBased on the above, we implement the algorithm as follows: \n1. Use a HashMap/dict to count the frequencies of the prefix sum of the running balance (bigger ones - smaller ones);\n2. If `k` is the median of a subarray, it must present in the subarray. Therefore, before finding the median, no subarray ending at current element meets the problem requirement; \n3. After finding `k`during traversal, no need to count the frequencies any more in the HashMap/dict. If `number of bigger ones == number of the smaller (or + 1)`, that is, `the difference between prefix sum of balances (bigger - smaller) is 0 or 1`, then `k`is the median of the subarray ending at current element;\n4. Use the difference of prefix sums to get the count of the required number of subarrays.\n\n----\n\n```java\n public int countSubarrays(int[] nums, int k) {\n Map<Integer, Integer> prefixSumOfBalance = new HashMap<>();\n prefixSumOfBalance.put(0, 1); // Dummy value of 0\'s frequency is 1.\n int ans = 0, runningBalance = 0;\n boolean found = false;\n for (int num : nums) {\n if (num < k) {\n --runningBalance;\n }else if (num > k) {\n ++runningBalance;\n }else {\n found = true;\n }\n if (found) {\n ans += prefixSumOfBalance.getOrDefault(runningBalance, 0) + prefixSumOfBalance.getOrDefault(runningBalance - 1, 0);\n }else {\n // prefixSumOfBalance.merge(runningBalance, 1, Integer::sum); // Similar to the following statement, but it is shorter.\n prefixSumOfBalance.put(runningBalance, prefixSumOfBalance.getOrDefault(runningBalance, 0) + 1);\n }\n }\n return ans;\n }\n```\n```python\n def countSubarrays(self, nums: List[int], k: int) -> int:\n prefix_sum_of_balance = Counter([0]) # Dummy value of 0\'s frequency is 1.\n running_balance = ans = 0\n found = False\n for num in nums:\n if num < k:\n running_balance -= 1\n elif num > k:\n running_balance += 1\n else:\n found = True\n if found:\n ans += prefix_sum_of_balance[running_balance] + prefix_sum_of_balance[running_balance - 1] \n else:\n prefix_sum_of_balance[running_balance] += 1\n return ans\n```\nCredit to **@Sung-Lin** for his code and explanation.\n```cpp\n/*\n [ 7, 1, 3, 4, 2, 5, 6], 4\n bal 1, 0, -1, -1, -2, -1, 0\n |<- cnt ->| \n ans 1. 0. 1. 2+1 \n -1 [4]\n -1 [4,2,5]\n 0 [3,4,2,5,6]\n 0 [7,1,3,4,2,5,6]\n -1 [4,2,5,6]\n \n cnt (prefix)\n 1: 1 (idx 0)\n 0: 2 (idx -1, 1)\n -1: 1 (idx 2)\n\n e.g. 4(idx 3) -> -1\n => find 3(idx 2) -> -1 => idx 2+1(=3) ~ idx 3 => balance == -1 - -1 == 0\n \n curBalance - x == 0 or 1\n => x == curBalance or x == curBalance - 1\n*/\nclass Solution {\npublic:\n int countSubarrays(vector<int>& nums, int k) {\n int n = (int) nums.size();\n \n unordered_map<int, int> cnt; // prefix\n cnt[0] = 1; // can be think as the prefix on index -1\n \n bool includeK = false;\n int balance = 0; \n \n int ans = 0;\n for (int i = 0; i < n; i++) {\n if (nums[i] < k)\n balance--;\n else if (nums[i] > k)\n balance++;\n else // num[i] == k\n includeK = true;\n \n if (includeK) {\n // find x in prefix hashmap \n // greater - smaller == 0 or 1\n // => prefix[i] - prefix[x] == 0 or 1\n // => curBalance - prefix[x] == 0 or curBalance - prefix[x] == 1\n // => prefix[x] == curBalance or prefix[x] == curBalance - 1\n ans += cnt[balance] + cnt[balance - 1]; \n }\n else\n cnt[balance]++;\n }\n return ans; \n }\n};\n```\n\n**Analysis:**\n\nTime & space: `O(n)`, where `n = nums.length`.

You are given an array `nums` of size `n` consisting of **distinct** integers from `1` to `n` and a positive integer `k`. Return _the number of non-empty subarrays in_ `nums` _that have a **median** equal to_ `k`. **Note**: * The median of an array is the **middle** element after sorting the array in **ascending** order. If the array is of even length, the median is the **left** middle element. * For example, the median of `[2,3,1,4]` is `2`, and the median of `[8,4,3,5,1]` is `4`. * A subarray is a contiguous part of an array. **Example 1:** **Input:** nums = \[3,2,1,4,5\], k = 4 **Output:** 3 **Explanation:** The subarrays that have a median equal to 4 are: \[4\], \[4,5\] and \[1,4,5\]. **Example 2:** **Input:** nums = \[2,3,1\], k = 3 **Output:** 1 **Explanation:** \[3\] is the only subarray that has a median equal to 3. **Constraints:** * `n == nums.length` * `1 <= n <= 105` * `1 <= nums[i], k <= n` * The integers in `nums` are distinct.

2 Sum || Prefix & Suffix || O(N)

count-subarrays-with-median-k

# Intuition\nWe can reduce this problem to a 2Sum after pre-processing \n\n# Approach\n\nlet idx be the index of k in nums\n1. find the prefix array where pre[i]= # of element > k - # of element < k in num[i:idx]\n2. find the suffix array where suf[i]= # of element > k - # of element < k in num[idx:i]\n\nif pre[i] + suf[j] = 0, for subarray nums[i:j+1], we have # of element > k = # of element < k ==> k is the median (for odd cases)\n\nsimilarly, if pre[i] + suf[j] = 1, for subarray nums[i:j+1], we have # of element > k = 1 + # of element < k ==> k is the median (for even cases)\n\nthen, we just need to find all (i,j) pair where pre[i] + suf[j] = 0 or 1\nthis becomes a 2Sum problem\n\n# Complexity\nO(N)\n\n# Code\n\n\n```\n def countSubarrays(self, nums: List[int], k: int) -> int:\n pre = defaultdict(int)\n suf = defaultdict(int)\n n = len(nums)\n idx = nums.index(k)\n\n cur = 0 # bigger - smaller\n for i in range(idx)[::-1]:\n cur += 1 if nums[i] > k else - 1\n pre[cur] += 1\n\n cur = 0 # smaller - bigger\n for i in range(idx + 1, n):\n cur += 1 if nums[i] < k else - 1\n suf[cur] += 1\n\n res = 1 + pre[0] + suf[0] + pre[1] + suf[-1]\n for k, v in pre.items():\n res += v * (suf[k]) + v * (suf[k - 1])\n\n return res\n```

You are given an array `nums` of size `n` consisting of **distinct** integers from `1` to `n` and a positive integer `k`. Return _the number of non-empty subarrays in_ `nums` _that have a **median** equal to_ `k`. **Note**: * The median of an array is the **middle** element after sorting the array in **ascending** order. If the array is of even length, the median is the **left** middle element. * For example, the median of `[2,3,1,4]` is `2`, and the median of `[8,4,3,5,1]` is `4`. * A subarray is a contiguous part of an array. **Example 1:** **Input:** nums = \[3,2,1,4,5\], k = 4 **Output:** 3 **Explanation:** The subarrays that have a median equal to 4 are: \[4\], \[4,5\] and \[1,4,5\]. **Example 2:** **Input:** nums = \[2,3,1\], k = 3 **Output:** 1 **Explanation:** \[3\] is the only subarray that has a median equal to 3. **Constraints:** * `n == nums.length` * `1 <= n <= 105` * `1 <= nums[i], k <= n` * The integers in `nums` are distinct.

[Python3] Counting O(N) With Explanations

count-subarrays-with-median-k

**Hint1:** We record 1 if `num > k`; -1 if `num < k`, and 0 if `num == k`.\n\n**Hint2:** Let `pos` denote the index of `k` in `nums`, where `k` is the median. Then the problem is equivalent to:\n1. `pos` is in the indices of the subarray;\n2. the sum of the subarray is either `0` or `1`.\n\n**Hint3:** Let `c_i` be the # of `num > k` - the # of `num < k` for `num` in `nums[pos..i]`. We count the frequencies of `c_i` using a hashmap `cnt`. Then, let `c_i` be the # of `num < k` - the # of `num > k` for `num` in `nums[i..pos]`.\nNow for each `i`,\n* `cnt[c_i]` is the number of valid subarrays with odd length in **Hint 2**\n* `cnt[c_i + 1]` is the number valid subarrays with even length in **Hint 2**\n\nWe can sum them up to get the final `ans`.\n\n**Complexity**\nTime Complexity: `O(n)`\nSpace Complexity: `O(n)`\n \n**Solution (credit to @endlesscheng)**\n```\nclass Solution:\n def countSubarrays(self, nums: List[int], k: int) -> int:\n\t\tpos = nums.index(k)\n cnt = defaultdict(int)\n cnt[0] = 1\n c = 0\n for i in range(pos + 1, len(nums)):\n c += 1 if nums[i] > k else -1\n cnt[c] += 1\n\n ans = cnt[0] + cnt[1]\n c = 0\n for i in range(pos - 1, -1, -1):\n c += 1 if nums[i] < k else -1\n ans += cnt[c] + cnt[c + 1]\n return ans\n```

You are given an array `nums` of size `n` consisting of **distinct** integers from `1` to `n` and a positive integer `k`. Return _the number of non-empty subarrays in_ `nums` _that have a **median** equal to_ `k`. **Note**: * The median of an array is the **middle** element after sorting the array in **ascending** order. If the array is of even length, the median is the **left** middle element. * For example, the median of `[2,3,1,4]` is `2`, and the median of `[8,4,3,5,1]` is `4`. * A subarray is a contiguous part of an array. **Example 1:** **Input:** nums = \[3,2,1,4,5\], k = 4 **Output:** 3 **Explanation:** The subarrays that have a median equal to 4 are: \[4\], \[4,5\] and \[1,4,5\]. **Example 2:** **Input:** nums = \[2,3,1\], k = 3 **Output:** 1 **Explanation:** \[3\] is the only subarray that has a median equal to 3. **Constraints:** * `n == nums.length` * `1 <= n <= 105` * `1 <= nums[i], k <= n` * The integers in `nums` are distinct.

[Python] O(n) Picture / Video Solution

count-subarrays-with-median-k

You can watch the [video](https://youtu.be/oLEKpPXUgm4) solution.\n\n# Conditions for valid subarray\n\n\n\n\nThe condition for a valid subarray:\n* Must include `K`\n* Difference in counts:\n\t* For **Odd length** subarray, ```no. of elements smaller than K = no. of elements greater than K ```\n\t* For **Even length** subarray, ```(no. of elements smaller than K) + 1 = no. of elements greater than K ```\n\n # Valid Subarrays\n\n\n\n# Counting pairs using our conditions\n\n\n\n\nSince we are dealing only with the difference between the count of **smaller** elements & **greater** elements, we can just store the difference between them for each index in our array starting from the **Median K**.\n\n```\nbal += 1 if num > k else (-1 if num < k else 0)\n```\n\nWe just have to do it for any one side ( let\'s assume right) from **Median K**. \n\n\n\n\nWe can store it in a HashMap where the key would be the `difference ( balance) ` and the value would be its `count`.\n\nWe now, have to go just left and using our conditions find pairs for both odd & even length.\n\nWhile going left, we have to calculate our `balance` on the fly, \n* for the odd length subarrays, we have to try to pair it with `cnt[-bal]`\n* for the even length subarrays, we have to try to pair it with `cnt[-bal + 1]`.\n\n\n# Time & Space Complexity\n\n`Time: O(n)` We are only going through the elements only once.\n\n`Space: O(n)` We are using a HashMap.\n\nIf you thought this was helpful, please upvote, like the video and subscribe to the channel.\n\nCheers.\n\n\n```\nclass Solution:\n def countSubarrays(self, nums: List[int], k: int) -> int:\n n = len(nums)\n pos = nums.index(k)\n \n cnt = defaultdict(int)\n \n bal=0\n for i in range(pos, n):\n num = nums[i]\n \n bal += 1 if num > k else (-1 if num < k else 0)\n cnt[bal] += 1\n \n res=0\n bal=0\n for i in reversed(range(pos+1)):\n num = nums[i]\n \n bal += 1 if num > k else (-1 if num < k else 0)\n \n res += cnt[-bal] # ODD\n res += cnt[-bal + 1] # EVEN\n \n return res\n\t

You are given an array `nums` of size `n` consisting of **distinct** integers from `1` to `n` and a positive integer `k`. Return _the number of non-empty subarrays in_ `nums` _that have a **median** equal to_ `k`. **Note**: * The median of an array is the **middle** element after sorting the array in **ascending** order. If the array is of even length, the median is the **left** middle element. * For example, the median of `[2,3,1,4]` is `2`, and the median of `[8,4,3,5,1]` is `4`. * A subarray is a contiguous part of an array. **Example 1:** **Input:** nums = \[3,2,1,4,5\], k = 4 **Output:** 3 **Explanation:** The subarrays that have a median equal to 4 are: \[4\], \[4,5\] and \[1,4,5\]. **Example 2:** **Input:** nums = \[2,3,1\], k = 3 **Output:** 1 **Explanation:** \[3\] is the only subarray that has a median equal to 3. **Constraints:** * `n == nums.length` * `1 <= n <= 105` * `1 <= nums[i], k <= n` * The integers in `nums` are distinct.

Python3 Solution With Freq Table

count-subarrays-with-median-k

\n\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countSubarrays(self, nums: List[int], k: int) -> int:\n idx,freq,prefix = nums.index(k), Counter(), 0\n for i in reversed(range(idx+1)): \n prefix += int(nums[i] > k) - int(nums[i] < k)\n freq[prefix] += 1\n res= prefix = 0 \n for i in range(idx, len(nums)): \n prefix += int(nums[i] > k) - int(nums[i] < k)\n res += freq[-prefix] + freq[-prefix+1]\n return res \n```

You are given an array `nums` of size `n` consisting of **distinct** integers from `1` to `n` and a positive integer `k`. Return _the number of non-empty subarrays in_ `nums` _that have a **median** equal to_ `k`. **Note**: * The median of an array is the **middle** element after sorting the array in **ascending** order. If the array is of even length, the median is the **left** middle element. * For example, the median of `[2,3,1,4]` is `2`, and the median of `[8,4,3,5,1]` is `4`. * A subarray is a contiguous part of an array. **Example 1:** **Input:** nums = \[3,2,1,4,5\], k = 4 **Output:** 3 **Explanation:** The subarrays that have a median equal to 4 are: \[4\], \[4,5\] and \[1,4,5\]. **Example 2:** **Input:** nums = \[2,3,1\], k = 3 **Output:** 1 **Explanation:** \[3\] is the only subarray that has a median equal to 3. **Constraints:** * `n == nums.length` * `1 <= n <= 105` * `1 <= nums[i], k <= n` * The integers in `nums` are distinct.

[C++|Java|Python3] split sentence into words

circular-sentence

**C++**\n```\nclass Solution {\npublic:\n bool isCircularSentence(string sentence) {\n vector<string> words; \n istringstream iss(sentence); \n string buff; \n while (iss >> buff) words.push_back(buff); \n for (int i = 0, n = words.size(); i < n; ++i) \n if (words[i].back() != words[(i+1) % n][0]) return false; \n return true; \n }\n};\n```\n**Java**\n```\nclass Solution {\n public boolean isCircularSentence(String sentence) {\n String[] words = sentence.split(" "); \n for (int i = 0, n = words.length; i < n; ++i) \n if (!words[i].endsWith(words[(i+1) % n].substring(0, 1))) return false; \n return true; \n }\n}\n```\n**Python3**\n```\nclass Solution:\n def isCircularSentence(self, sentence: str) -> bool:\n words = sentence.split()\n return all(w[-1] == words[(i+1) % len(words)][0] for i, w in enumerate(words))\n```

A **sentence** is a list of words that are separated by a **single** space with no leading or trailing spaces. * For example, `"Hello World "`, `"HELLO "`, `"hello world hello world "` are all sentences. Words consist of **only** uppercase and lowercase English letters. Uppercase and lowercase English letters are considered different. A sentence is **circular** if: * The last character of a word is equal to the first character of the next word. * The last character of the last word is equal to the first character of the first word. For example, `"leetcode exercises sound delightful "`, `"eetcode "`, `"leetcode eats soul "` are all circular sentences. However, `"Leetcode is cool "`, `"happy Leetcode "`, `"Leetcode "` and `"I like Leetcode "` are **not** circular sentences. Given a string `sentence`, return `true` _if it is circular_. Otherwise, return `false`. **Example 1:** **Input:** sentence = "leetcode exercises sound delightful " **Output:** true **Explanation:** The words in sentence are \[ "leetcode ", "exercises ", "sound ", "delightful "\]. - leetcode's last character is equal to exercises's first character. - exercises's last character is equal to sound's first character. - sound's last character is equal to delightful's first character. - delightful's last character is equal to leetcode's first character. The sentence is circular. **Example 2:** **Input:** sentence = "eetcode " **Output:** true **Explanation:** The words in sentence are \[ "eetcode "\]. - eetcode's last character is equal to eetcode's first character. The sentence is circular. **Example 3:** **Input:** sentence = "Leetcode is cool " **Output:** false **Explanation:** The words in sentence are \[ "Leetcode ", "is ", "cool "\]. - Leetcode's last character is **not** equal to is's first character. The sentence is **not** circular. **Constraints:** * `1 <= sentence.length <= 500` * `sentence` consist of only lowercase and uppercase English letters and spaces. * The words in `sentence` are separated by a single space. * There are no leading or trailing spaces.

Python - Two Approaches

circular-sentence

Without **Split** Space `O(1`)\n```\nclass Solution:\n def isCircularSentence(self, sentence: str) -> bool:\n for i in range(len(sentence)):\n if sentence[i] == " ":\n if sentence[i-1] != sentence[i+1]:\n return False\n return sentence[0] == sentence[-1]\n```\n\n\nUsing **Split** Space `O(n)`\n```\nclass Solution:\n def isCircularSentence(self, sentence: str) -> bool:\n words = sentence.split(\' \')\n prev = words[0]\n \n for w in words[1:]:\n if w[0]!=prev[-1]:\n return False\n prev = w\n \n return sentence[0]==sentence[-1]

A **sentence** is a list of words that are separated by a **single** space with no leading or trailing spaces. * For example, `"Hello World "`, `"HELLO "`, `"hello world hello world "` are all sentences. Words consist of **only** uppercase and lowercase English letters. Uppercase and lowercase English letters are considered different. A sentence is **circular** if: * The last character of a word is equal to the first character of the next word. * The last character of the last word is equal to the first character of the first word. For example, `"leetcode exercises sound delightful "`, `"eetcode "`, `"leetcode eats soul "` are all circular sentences. However, `"Leetcode is cool "`, `"happy Leetcode "`, `"Leetcode "` and `"I like Leetcode "` are **not** circular sentences. Given a string `sentence`, return `true` _if it is circular_. Otherwise, return `false`. **Example 1:** **Input:** sentence = "leetcode exercises sound delightful " **Output:** true **Explanation:** The words in sentence are \[ "leetcode ", "exercises ", "sound ", "delightful "\]. - leetcode's last character is equal to exercises's first character. - exercises's last character is equal to sound's first character. - sound's last character is equal to delightful's first character. - delightful's last character is equal to leetcode's first character. The sentence is circular. **Example 2:** **Input:** sentence = "eetcode " **Output:** true **Explanation:** The words in sentence are \[ "eetcode "\]. - eetcode's last character is equal to eetcode's first character. The sentence is circular. **Example 3:** **Input:** sentence = "Leetcode is cool " **Output:** false **Explanation:** The words in sentence are \[ "Leetcode ", "is ", "cool "\]. - Leetcode's last character is **not** equal to is's first character. The sentence is **not** circular. **Constraints:** * `1 <= sentence.length <= 500` * `sentence` consist of only lowercase and uppercase English letters and spaces. * The words in `sentence` are separated by a single space. * There are no leading or trailing spaces.

Simple and Easy to Understand | Two Solutions | Python

circular-sentence

##### Solution 1:\n* *Time Complexity :* **O(N)**\n* *Space Complexity:* **O(1)**\n```\nclass Solution(object):\n def isCircularSentence(self, s):\n if s[0] != s[-1]: return False\n flag = 1\n for ch in s:\n if flag:\n if ch != \' \': last = ch\n else: flag = 0\n else:\n if ch != last: return False\n flag = 1\n return True\n```\n##### Solution 2:\n* *Time Complexity :* **O(N)**\n* *Space Complexity:* **O(N)**\n```\nclass Solution(object):\n def isCircularSentence(self, s):\n arr, word = [], \'\'\n for ch in s:\n if ch == \' \':\n arr.append(word)\n word = \'\'\n else: word += ch\n arr.append(word)\n if arr[0][0] != arr[-1][-1]:\n return False\n last = arr[0][-1] \n for i in range(1, len(arr)):\n if arr[i][0] == last:\n last = arr[i][-1]\n else:\n return False\n return True\n```\n**UpVote**, if you like it **:)**

A **sentence** is a list of words that are separated by a **single** space with no leading or trailing spaces. * For example, `"Hello World "`, `"HELLO "`, `"hello world hello world "` are all sentences. Words consist of **only** uppercase and lowercase English letters. Uppercase and lowercase English letters are considered different. A sentence is **circular** if: * The last character of a word is equal to the first character of the next word. * The last character of the last word is equal to the first character of the first word. For example, `"leetcode exercises sound delightful "`, `"eetcode "`, `"leetcode eats soul "` are all circular sentences. However, `"Leetcode is cool "`, `"happy Leetcode "`, `"Leetcode "` and `"I like Leetcode "` are **not** circular sentences. Given a string `sentence`, return `true` _if it is circular_. Otherwise, return `false`. **Example 1:** **Input:** sentence = "leetcode exercises sound delightful " **Output:** true **Explanation:** The words in sentence are \[ "leetcode ", "exercises ", "sound ", "delightful "\]. - leetcode's last character is equal to exercises's first character. - exercises's last character is equal to sound's first character. - sound's last character is equal to delightful's first character. - delightful's last character is equal to leetcode's first character. The sentence is circular. **Example 2:** **Input:** sentence = "eetcode " **Output:** true **Explanation:** The words in sentence are \[ "eetcode "\]. - eetcode's last character is equal to eetcode's first character. The sentence is circular. **Example 3:** **Input:** sentence = "Leetcode is cool " **Output:** false **Explanation:** The words in sentence are \[ "Leetcode ", "is ", "cool "\]. - Leetcode's last character is **not** equal to is's first character. The sentence is **not** circular. **Constraints:** * `1 <= sentence.length <= 500` * `sentence` consist of only lowercase and uppercase English letters and spaces. * The words in `sentence` are separated by a single space. * There are no leading or trailing spaces.

Python | Easy Solution✅

circular-sentence

# Code\u2705\n```\nclass Solution:\n def isCircularSentence(self, sentence: str) -> bool: #// sentence = "leetcode exercises sound delightful"\n sentence_list = list(sentence.split(" ")) #// sentence_list = [\'leetcode\', \'exercises\', \'sound\', \'delightful\'] \n current = "" #// LOOP 1 LOOP 2\n for index, word in enumerate(sentence_list): #// when index = 0 and word = leetcode when index = 1 and word = exercises\n if current and current != word[0]: #// condition not met as current = "" current = "e" and current = word[0]\n return False\n current = word[-1] #// current = \'e\' now current = \'s\' now\n if index == len(sentence_list)-1 and current != sentence_list[0][0]: #// this condition will satisfy when index = 3 and current = l of leetcode (first word in sentence_list)\n return False\n return True\n```

A **sentence** is a list of words that are separated by a **single** space with no leading or trailing spaces. * For example, `"Hello World "`, `"HELLO "`, `"hello world hello world "` are all sentences. Words consist of **only** uppercase and lowercase English letters. Uppercase and lowercase English letters are considered different. A sentence is **circular** if: * The last character of a word is equal to the first character of the next word. * The last character of the last word is equal to the first character of the first word. For example, `"leetcode exercises sound delightful "`, `"eetcode "`, `"leetcode eats soul "` are all circular sentences. However, `"Leetcode is cool "`, `"happy Leetcode "`, `"Leetcode "` and `"I like Leetcode "` are **not** circular sentences. Given a string `sentence`, return `true` _if it is circular_. Otherwise, return `false`. **Example 1:** **Input:** sentence = "leetcode exercises sound delightful " **Output:** true **Explanation:** The words in sentence are \[ "leetcode ", "exercises ", "sound ", "delightful "\]. - leetcode's last character is equal to exercises's first character. - exercises's last character is equal to sound's first character. - sound's last character is equal to delightful's first character. - delightful's last character is equal to leetcode's first character. The sentence is circular. **Example 2:** **Input:** sentence = "eetcode " **Output:** true **Explanation:** The words in sentence are \[ "eetcode "\]. - eetcode's last character is equal to eetcode's first character. The sentence is circular. **Example 3:** **Input:** sentence = "Leetcode is cool " **Output:** false **Explanation:** The words in sentence are \[ "Leetcode ", "is ", "cool "\]. - Leetcode's last character is **not** equal to is's first character. The sentence is **not** circular. **Constraints:** * `1 <= sentence.length <= 500` * `sentence` consist of only lowercase and uppercase English letters and spaces. * The words in `sentence` are separated by a single space. * There are no leading or trailing spaces.

Python solution with split and zip

circular-sentence

\n# Code\n```python\nclass Solution:\n def isCircularSentence(self, sentence: str) -> bool:\n words = sentence.split()\n \n for prev, curr in zip(words, words[1:]):\n if prev[-1] != curr[0]:\n return False\n return words[0][0] == words[-1][-1]\n```

A **sentence** is a list of words that are separated by a **single** space with no leading or trailing spaces. * For example, `"Hello World "`, `"HELLO "`, `"hello world hello world "` are all sentences. Words consist of **only** uppercase and lowercase English letters. Uppercase and lowercase English letters are considered different. A sentence is **circular** if: * The last character of a word is equal to the first character of the next word. * The last character of the last word is equal to the first character of the first word. For example, `"leetcode exercises sound delightful "`, `"eetcode "`, `"leetcode eats soul "` are all circular sentences. However, `"Leetcode is cool "`, `"happy Leetcode "`, `"Leetcode "` and `"I like Leetcode "` are **not** circular sentences. Given a string `sentence`, return `true` _if it is circular_. Otherwise, return `false`. **Example 1:** **Input:** sentence = "leetcode exercises sound delightful " **Output:** true **Explanation:** The words in sentence are \[ "leetcode ", "exercises ", "sound ", "delightful "\]. - leetcode's last character is equal to exercises's first character. - exercises's last character is equal to sound's first character. - sound's last character is equal to delightful's first character. - delightful's last character is equal to leetcode's first character. The sentence is circular. **Example 2:** **Input:** sentence = "eetcode " **Output:** true **Explanation:** The words in sentence are \[ "eetcode "\]. - eetcode's last character is equal to eetcode's first character. The sentence is circular. **Example 3:** **Input:** sentence = "Leetcode is cool " **Output:** false **Explanation:** The words in sentence are \[ "Leetcode ", "is ", "cool "\]. - Leetcode's last character is **not** equal to is's first character. The sentence is **not** circular. **Constraints:** * `1 <= sentence.length <= 500` * `sentence` consist of only lowercase and uppercase English letters and spaces. * The words in `sentence` are separated by a single space. * There are no leading or trailing spaces.

Java and Python Solution

circular-sentence

# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\no(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Java\n```\nclass Solution {\n public boolean isCircularSentence(String sentence) {\n String[] words = sentence.split(" ");\n String lastWord = words[words.length-1];\n String firstWord = words[0];\n if(firstWord.charAt(0) != lastWord.charAt(lastWord.length()-1)){\n return false;\n }\n for(int i = 0; i < words.length-1; i++){\n if(words[i].charAt(words[i].length()-1) != words[i+1].charAt(0)){\n return false;\n }\n }\n return true;\n }\n}\n```\n\n# Python\n```\nclass Solution:\n def isCircularSentence(self, sentence: str) -> bool:\n words = sentence.split()\n print(words)\n if words[0][0] != words[-1][-1]:\n return False\n for i in range(len(words) - 1):\n if words[i][-1] != words[i+1][0]:\n return False\n return True \n```

A **sentence** is a list of words that are separated by a **single** space with no leading or trailing spaces. * For example, `"Hello World "`, `"HELLO "`, `"hello world hello world "` are all sentences. Words consist of **only** uppercase and lowercase English letters. Uppercase and lowercase English letters are considered different. A sentence is **circular** if: * The last character of a word is equal to the first character of the next word. * The last character of the last word is equal to the first character of the first word. For example, `"leetcode exercises sound delightful "`, `"eetcode "`, `"leetcode eats soul "` are all circular sentences. However, `"Leetcode is cool "`, `"happy Leetcode "`, `"Leetcode "` and `"I like Leetcode "` are **not** circular sentences. Given a string `sentence`, return `true` _if it is circular_. Otherwise, return `false`. **Example 1:** **Input:** sentence = "leetcode exercises sound delightful " **Output:** true **Explanation:** The words in sentence are \[ "leetcode ", "exercises ", "sound ", "delightful "\]. - leetcode's last character is equal to exercises's first character. - exercises's last character is equal to sound's first character. - sound's last character is equal to delightful's first character. - delightful's last character is equal to leetcode's first character. The sentence is circular. **Example 2:** **Input:** sentence = "eetcode " **Output:** true **Explanation:** The words in sentence are \[ "eetcode "\]. - eetcode's last character is equal to eetcode's first character. The sentence is circular. **Example 3:** **Input:** sentence = "Leetcode is cool " **Output:** false **Explanation:** The words in sentence are \[ "Leetcode ", "is ", "cool "\]. - Leetcode's last character is **not** equal to is's first character. The sentence is **not** circular. **Constraints:** * `1 <= sentence.length <= 500` * `sentence` consist of only lowercase and uppercase English letters and spaces. * The words in `sentence` are separated by a single space. * There are no leading or trailing spaces.

Python mod division to wrap around

circular-sentence

# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFor a sentence of n words, it requires evaluation of adjacent characters $$n$$ times. \n\nSince the iteration is circular, using mod division is helpful in handling wrap around. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nSuppose there are $$M$$ characters and $$N$$ words in total. \n\n$$O(M)$$ for splitting into words, $$O(N)$$ for going through the first and last character of each word. \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(M)$$ for storing the spitted result of the sentence.\n# Code\n```\nclass Solution:\n def isCircularSentence(self, sentence: str) -> bool:\n """for a sentence of n words, evaluate n times"""\n words = sentence.split(\' \')\n n = len(words)\n for i in range(n):\n if words[i%n][-1] != words[(i+1)%n][0]:\n return False\n else:\n return True\n\n\n\n```

A **sentence** is a list of words that are separated by a **single** space with no leading or trailing spaces. * For example, `"Hello World "`, `"HELLO "`, `"hello world hello world "` are all sentences. Words consist of **only** uppercase and lowercase English letters. Uppercase and lowercase English letters are considered different. A sentence is **circular** if: * The last character of a word is equal to the first character of the next word. * The last character of the last word is equal to the first character of the first word. For example, `"leetcode exercises sound delightful "`, `"eetcode "`, `"leetcode eats soul "` are all circular sentences. However, `"Leetcode is cool "`, `"happy Leetcode "`, `"Leetcode "` and `"I like Leetcode "` are **not** circular sentences. Given a string `sentence`, return `true` _if it is circular_. Otherwise, return `false`. **Example 1:** **Input:** sentence = "leetcode exercises sound delightful " **Output:** true **Explanation:** The words in sentence are \[ "leetcode ", "exercises ", "sound ", "delightful "\]. - leetcode's last character is equal to exercises's first character. - exercises's last character is equal to sound's first character. - sound's last character is equal to delightful's first character. - delightful's last character is equal to leetcode's first character. The sentence is circular. **Example 2:** **Input:** sentence = "eetcode " **Output:** true **Explanation:** The words in sentence are \[ "eetcode "\]. - eetcode's last character is equal to eetcode's first character. The sentence is circular. **Example 3:** **Input:** sentence = "Leetcode is cool " **Output:** false **Explanation:** The words in sentence are \[ "Leetcode ", "is ", "cool "\]. - Leetcode's last character is **not** equal to is's first character. The sentence is **not** circular. **Constraints:** * `1 <= sentence.length <= 500` * `sentence` consist of only lowercase and uppercase English letters and spaces. * The words in `sentence` are separated by a single space. * There are no leading or trailing spaces.

Simple Python solution using sorting

divide-players-into-teams-of-equal-skill

\n\n# Code\n```\nclass Solution:\n def dividePlayers(self, A: List[int]) -> int:\n A.sort()\n n = len(A)\n a = [A[i]+A[n-i-1] for i in range(n//2)]\n if len(set(a)) != 1: return -1\n return sum(A[i]*A[n-i-1] for i in range(n//2)) \n```

You are given a positive integer array `skill` of **even** length `n` where `skill[i]` denotes the skill of the `ith` player. Divide the players into `n / 2` teams of size `2` such that the total skill of each team is **equal**. The **chemistry** of a team is equal to the **product** of the skills of the players on that team. Return _the sum of the **chemistry** of all the teams, or return_ `-1` _if there is no way to divide the players into teams such that the total skill of each team is equal._ **Example 1:** **Input:** skill = \[3,2,5,1,3,4\] **Output:** 22 **Explanation:** Divide the players into the following teams: (1, 5), (2, 4), (3, 3), where each team has a total skill of 6. The sum of the chemistry of all the teams is: 1 \* 5 + 2 \* 4 + 3 \* 3 = 5 + 8 + 9 = 22. **Example 2:** **Input:** skill = \[3,4\] **Output:** 12 **Explanation:** The two players form a team with a total skill of 7. The chemistry of the team is 3 \* 4 = 12. **Example 3:** **Input:** skill = \[1,1,2,3\] **Output:** -1 **Explanation:** There is no way to divide the players into teams such that the total skill of each team is equal. **Constraints:** * `2 <= skill.length <= 105` * `skill.length` is even. * `1 <= skill[i] <= 1000`

simple python solution || brute force method

divide-players-into-teams-of-equal-skill

**upvote if u like the solution**\n```\n dum=0\n k=sum(skill)\n if len(skill)==2:\n return skill[0]*skill[1]\n elif len(skill)%2==0 and sum(skill)%(len(skill)/2)==0:\n ratio=k/(len(skill)/2)\n else:\n return -1\n skill.sort()\n for i in range(len(skill)//2):\n if skill[i]+skill[len(skill)-(i+1)]!=ratio:\n return -1\n dum+=skill[i]*skill[len(skill)-(i+1)]\n return dum\n```

You are given a positive integer array `skill` of **even** length `n` where `skill[i]` denotes the skill of the `ith` player. Divide the players into `n / 2` teams of size `2` such that the total skill of each team is **equal**. The **chemistry** of a team is equal to the **product** of the skills of the players on that team. Return _the sum of the **chemistry** of all the teams, or return_ `-1` _if there is no way to divide the players into teams such that the total skill of each team is equal._ **Example 1:** **Input:** skill = \[3,2,5,1,3,4\] **Output:** 22 **Explanation:** Divide the players into the following teams: (1, 5), (2, 4), (3, 3), where each team has a total skill of 6. The sum of the chemistry of all the teams is: 1 \* 5 + 2 \* 4 + 3 \* 3 = 5 + 8 + 9 = 22. **Example 2:** **Input:** skill = \[3,4\] **Output:** 12 **Explanation:** The two players form a team with a total skill of 7. The chemistry of the team is 3 \* 4 = 12. **Example 3:** **Input:** skill = \[1,1,2,3\] **Output:** -1 **Explanation:** There is no way to divide the players into teams such that the total skill of each team is equal. **Constraints:** * `2 <= skill.length <= 105` * `skill.length` is even. * `1 <= skill[i] <= 1000`

[C++|Java|Python3] freq table

divide-players-into-teams-of-equal-skill

**C++**\n```\nclass Solution {\npublic:\n long long dividePlayers(vector<int>& skill) {\n int val = 2*accumulate(skill.begin(), skill.end(), 0) / skill.size(); \n long long ans = 0; \n unordered_map<int, int> freq; \n for (auto& x : skill) ++freq[x]; \n for (auto& [k, v] : freq) {\n if (v != freq[val-k]) return -1; \n ans += (long long) k * (val - k) * v; \n }\n return ans/2; \n }\n};\n```\n**Java**\n```\nclass Solution {\n public long dividePlayers(int[] skill) {\n int val = 2*Arrays.stream(skill).sum() / skill.length; \n long ans = 0; \n HashMap<Integer, Integer> freq = new HashMap<>(); \n for (int x : skill) freq.merge(x, 1, Integer::sum); \n for (Map.Entry<Integer, Integer> entry : freq.entrySet()) {\n int k = entry.getKey(), v = entry.getValue(); \n if (v != freq.getOrDefault(val-k, 0)) return -1; \n ans += (long) k*(val-k)*v; \n }\n return ans/2;\n }\n}\n```\n**Python3**\n```\nclass Solution:\n def dividePlayers(self, skill: List[int]) -> int:\n ans = 0 \n val = 2*sum(skill) // len(skill)\n freq = Counter(skill)\n for i, (k, v) in enumerate(freq.items()):\n if v != freq[val - k]: return -1 \n ans += k*(val-k)*v\n return ans // 2\n```

You are given a positive integer array `skill` of **even** length `n` where `skill[i]` denotes the skill of the `ith` player. Divide the players into `n / 2` teams of size `2` such that the total skill of each team is **equal**. The **chemistry** of a team is equal to the **product** of the skills of the players on that team. Return _the sum of the **chemistry** of all the teams, or return_ `-1` _if there is no way to divide the players into teams such that the total skill of each team is equal._ **Example 1:** **Input:** skill = \[3,2,5,1,3,4\] **Output:** 22 **Explanation:** Divide the players into the following teams: (1, 5), (2, 4), (3, 3), where each team has a total skill of 6. The sum of the chemistry of all the teams is: 1 \* 5 + 2 \* 4 + 3 \* 3 = 5 + 8 + 9 = 22. **Example 2:** **Input:** skill = \[3,4\] **Output:** 12 **Explanation:** The two players form a team with a total skill of 7. The chemistry of the team is 3 \* 4 = 12. **Example 3:** **Input:** skill = \[1,1,2,3\] **Output:** -1 **Explanation:** There is no way to divide the players into teams such that the total skill of each team is equal. **Constraints:** * `2 <= skill.length <= 105` * `skill.length` is even. * `1 <= skill[i] <= 1000`

Simple O(N) Solution | No sorting (Two Sum Technique)

divide-players-into-teams-of-equal-skill

## Time Complexity = O(N)\n## Space Complexity = O(N)\n\n```python\nclass Solution:\n def dividePlayers(self, skill: List[int]) -> int:\n \n n = len(skill)\n t = n//2 # how many pairs will be created\n s = sum(skill) // t # what will be sum of each pair\n \n c = Counter(skill) # keep track of how many numbers we have\n lookup =Counter() # keep track of how many pairs generated\n \n for num in skill:\n # If we have number and equal can be generated from that number the make a pair\n if c[num] and s- num in c and c[s-num]>0:\n c[s-num]-=1\n c[num]-=1\n lookup[(s-num, num)]+=1\n \n # If some number is unused then return -1\n for k, v in c.items():\n if v!= 0:\n return -1\n\n # Calculate result as told\n result = 0\n for k,v in lookup.items():\n a, b = k\n # multiplying by v because that\'s number of pairs\n result += a*b*v\n \n return result\n```

You are given a positive integer array `skill` of **even** length `n` where `skill[i]` denotes the skill of the `ith` player. Divide the players into `n / 2` teams of size `2` such that the total skill of each team is **equal**. The **chemistry** of a team is equal to the **product** of the skills of the players on that team. Return _the sum of the **chemistry** of all the teams, or return_ `-1` _if there is no way to divide the players into teams such that the total skill of each team is equal._ **Example 1:** **Input:** skill = \[3,2,5,1,3,4\] **Output:** 22 **Explanation:** Divide the players into the following teams: (1, 5), (2, 4), (3, 3), where each team has a total skill of 6. The sum of the chemistry of all the teams is: 1 \* 5 + 2 \* 4 + 3 \* 3 = 5 + 8 + 9 = 22. **Example 2:** **Input:** skill = \[3,4\] **Output:** 12 **Explanation:** The two players form a team with a total skill of 7. The chemistry of the team is 3 \* 4 = 12. **Example 3:** **Input:** skill = \[1,1,2,3\] **Output:** -1 **Explanation:** There is no way to divide the players into teams such that the total skill of each team is equal. **Constraints:** * `2 <= skill.length <= 105` * `skill.length` is even. * `1 <= skill[i] <= 1000`

Python3 O(nlogn) Sorting | Easy to understand

divide-players-into-teams-of-equal-skill

# Code\n```\nclass Solution:\n def dividePlayers(self, skill: List[int]) -> int:\n n = len(skill)\n skill.sort()\n res = 0\n for i in range(0, n//2):\n if skill[i] + skill[n-i-1] != skill[0] + skill[-1]:\n return -1\n res += (skill[i] * skill[n-i-1])\n return res\n \n```

You are given a positive integer array `skill` of **even** length `n` where `skill[i]` denotes the skill of the `ith` player. Divide the players into `n / 2` teams of size `2` such that the total skill of each team is **equal**. The **chemistry** of a team is equal to the **product** of the skills of the players on that team. Return _the sum of the **chemistry** of all the teams, or return_ `-1` _if there is no way to divide the players into teams such that the total skill of each team is equal._ **Example 1:** **Input:** skill = \[3,2,5,1,3,4\] **Output:** 22 **Explanation:** Divide the players into the following teams: (1, 5), (2, 4), (3, 3), where each team has a total skill of 6. The sum of the chemistry of all the teams is: 1 \* 5 + 2 \* 4 + 3 \* 3 = 5 + 8 + 9 = 22. **Example 2:** **Input:** skill = \[3,4\] **Output:** 12 **Explanation:** The two players form a team with a total skill of 7. The chemistry of the team is 3 \* 4 = 12. **Example 3:** **Input:** skill = \[1,1,2,3\] **Output:** -1 **Explanation:** There is no way to divide the players into teams such that the total skill of each team is equal. **Constraints:** * `2 <= skill.length <= 105` * `skill.length` is even. * `1 <= skill[i] <= 1000`

divide-players-into-teams-of-equal-skill

divide-players-into-teams-of-equal-skill

\n# Code\n```\nclass Solution:\n def dividePlayers(self, s: List[int]) -> int:\n s.sort()\n l = 0\n r = len(s)-1\n p = []\n f = []\n while l< len(s)/2:\n p.append(s[l] * s[r])\n f.append(s[l] + s[r])\n l+=1\n r-=1\n if len(set(f))==1:\n return (sum(p))\n else:\n return (-1)\n```

You are given a positive integer array `skill` of **even** length `n` where `skill[i]` denotes the skill of the `ith` player. Divide the players into `n / 2` teams of size `2` such that the total skill of each team is **equal**. The **chemistry** of a team is equal to the **product** of the skills of the players on that team. Return _the sum of the **chemistry** of all the teams, or return_ `-1` _if there is no way to divide the players into teams such that the total skill of each team is equal._ **Example 1:** **Input:** skill = \[3,2,5,1,3,4\] **Output:** 22 **Explanation:** Divide the players into the following teams: (1, 5), (2, 4), (3, 3), where each team has a total skill of 6. The sum of the chemistry of all the teams is: 1 \* 5 + 2 \* 4 + 3 \* 3 = 5 + 8 + 9 = 22. **Example 2:** **Input:** skill = \[3,4\] **Output:** 12 **Explanation:** The two players form a team with a total skill of 7. The chemistry of the team is 3 \* 4 = 12. **Example 3:** **Input:** skill = \[1,1,2,3\] **Output:** -1 **Explanation:** There is no way to divide the players into teams such that the total skill of each team is equal. **Constraints:** * `2 <= skill.length <= 105` * `skill.length` is even. * `1 <= skill[i] <= 1000`

Solution using dsu beats 100% space and 100% runtime.

minimum-score-of-a-path-between-two-cities

# Intuition\nThe ans will be the minimum weight edge in component containing 1 and n.\n\n# Approach\nsimply add minimum array(let it be m) to dsu class.Where m[i] will denote minimum weight of the component i if i is parent, when we add a new edge [a,b,weight] and take i (it may be a or b decide by size) as parent node relation will be - m[i]=min(m[a],m[b],weight)\n\n# Complexity\n- Time complexity:\no(e+n)\n- Space complexity:\no(n)\n\n# Code\n```\nclass dsu:\n def __init__(self,n):\n self.size=[1]*(n+1)\n self.parent=[x for x in range(n+1)]\n self.m=[float("inf") for x in range(n+1)]\n def find(self,x):\n if x==self.parent[x]:\n return x\n self.parent[x]=dsu.find(self,self.parent[x])\n return self.parent[x]\n def f(self):\n return self.m[dsu.find(self,1)]\n def union(self,u,v,w):\n x=dsu.find(self,u)\n y=dsu.find(self,v)\n if x==y:\n self.m[x]=min(self.m[x],w)\n return\n elif self.size[x]>self.size[y]:\n self.size[x]+=self.size[y]\n self.parent[y]=x\n self.m[x]=min(self.m[x],w,self.m[y])\n else:\n self.size[y]+=self.size[x]\n self.parent[x]=y\n self.m[y]=min(self.m[y],w,self.m[x])\nclass Solution:\n def minScore(self, n: int, roads: List[List[int]]) -> int:\n d=dsu(n)\n for i in range(len(roads)):\n d.union(roads[i][0],roads[i][1],roads[i][2])\n return d.f()\n```

You are given a positive integer `n` representing `n` cities numbered from `1` to `n`. You are also given a **2D** array `roads` where `roads[i] = [ai, bi, distancei]` indicates that there is a **bidirectional** road between cities `ai` and `bi` with a distance equal to `distancei`. The cities graph is not necessarily connected. The **score** of a path between two cities is defined as the **minimum** distance of a road in this path. Return _the **minimum** possible score of a path between cities_ `1` _and_ `n`. **Note**: * A path is a sequence of roads between two cities. * It is allowed for a path to contain the same road **multiple** times, and you can visit cities `1` and `n` multiple times along the path. * The test cases are generated such that there is **at least** one path between `1` and `n`. **Example 1:** **Input:** n = 4, roads = \[\[1,2,9\],\[2,3,6\],\[2,4,5\],\[1,4,7\]\] **Output:** 5 **Explanation:** The path from city 1 to 4 with the minimum score is: 1 -> 2 -> 4. The score of this path is min(9,5) = 5. It can be shown that no other path has less score. **Example 2:** **Input:** n = 4, roads = \[\[1,2,2\],\[1,3,4\],\[3,4,7\]\] **Output:** 2 **Explanation:** The path from city 1 to 4 with the minimum score is: 1 -> 2 -> 1 -> 3 -> 4. The score of this path is min(2,2,4,7) = 2. **Constraints:** * `2 <= n <= 105` * `1 <= roads.length <= 105` * `roads[i].length == 3` * `1 <= ai, bi <= n` * `ai != bi` * `1 <= distancei <= 104` * There are no repeated edges. * There is at least one path between `1` and `n`.

Python3 👍||⚡99/96 T/M faster beats🔥|| clean solution || simple explain ||

minimum-score-of-a-path-between-two-cities

\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nImportant tips for you : As there is at least one path between 1 and n , just find out all the edges that can be reached from node 1 and return the minimum edge.\n\n# Complexity\n- Time complexity:O(n)\n- create table time , bfs time , traval roads time\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n- hash table\u3001view\u3001ans\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minScore(self, n: int, roads: List[List[int]]) -> int:\n ht = defaultdict(list)\n for i,j,dis in roads:\n ht[i].append(j)\n ht[j].append(i)\n ans,view= inf,set()\n queue = deque([1])\n while queue:\n cur_city = queue.popleft()\n for next_city in ht[cur_city]:\n if next_city not in view:\n queue.append(next_city)\n view.add(next_city)\n for i,j,dis in roads:\n if i in view or j in view:\n ans=min(ans,dis)\n return ans\n```

You are given a positive integer `n` representing `n` cities numbered from `1` to `n`. You are also given a **2D** array `roads` where `roads[i] = [ai, bi, distancei]` indicates that there is a **bidirectional** road between cities `ai` and `bi` with a distance equal to `distancei`. The cities graph is not necessarily connected. The **score** of a path between two cities is defined as the **minimum** distance of a road in this path. Return _the **minimum** possible score of a path between cities_ `1` _and_ `n`. **Note**: * A path is a sequence of roads between two cities. * It is allowed for a path to contain the same road **multiple** times, and you can visit cities `1` and `n` multiple times along the path. * The test cases are generated such that there is **at least** one path between `1` and `n`. **Example 1:** **Input:** n = 4, roads = \[\[1,2,9\],\[2,3,6\],\[2,4,5\],\[1,4,7\]\] **Output:** 5 **Explanation:** The path from city 1 to 4 with the minimum score is: 1 -> 2 -> 4. The score of this path is min(9,5) = 5. It can be shown that no other path has less score. **Example 2:** **Input:** n = 4, roads = \[\[1,2,2\],\[1,3,4\],\[3,4,7\]\] **Output:** 2 **Explanation:** The path from city 1 to 4 with the minimum score is: 1 -> 2 -> 1 -> 3 -> 4. The score of this path is min(2,2,4,7) = 2. **Constraints:** * `2 <= n <= 105` * `1 <= roads.length <= 105` * `roads[i].length == 3` * `1 <= ai, bi <= n` * `ai != bi` * `1 <= distancei <= 104` * There are no repeated edges. * There is at least one path between `1` and `n`.

[C++|Python3] dfs + bfs

divide-nodes-into-the-maximum-number-of-groups

\n**Intuition**\n1) If there is a odd-length cycle, it is impossible to divide the nodes, which is checked by the DFS part; \n2) If it is possible, then we can enumerate all nodes via BFS to check for the largest number of division along each connected component, which is computed by the BFS part. \n\n**Implementation**\n**C++**\n```\nclass Solution {\npublic:\n int magnificentSets(int n, vector<vector<int>>& edges) {\n vector<vector<int>> graph(n); \n for (auto& e : edges) {\n graph[e[0]-1].push_back(e[1]-1); \n graph[e[1]-1].push_back(e[0]-1); \n }\n \n vector<int> seen(n); \n vector<vector<int>> group; \n for (int i = 0; i < n; ++i) \n if (!seen[i]) {\n seen[i] = 1; \n stack<int> stk; stk.push(i); \n group.push_back({i}); \n while (stk.size()) {\n auto u = stk.top(); stk.pop(); \n for (auto& v : graph[u]) \n if (!seen[v]) {\n seen[v] = seen[u] + 1; \n stk.push(v); \n group.back().push_back(v); \n } else if ((seen[u] & 1) == (seen[v] & 1)) return -1; \n }\n }\n \n auto bfs = [&](int x) {\n int ans = 0; \n vector<bool> seen(n); \n seen[x] = true; \n queue<int> q; q.push(x); \n for (; q.size(); ++ans) \n for (int sz = q.size(); sz; --sz) {\n auto u = q.front(); q.pop(); \n for (auto& v : graph[u]) \n if (!seen[v]) {\n seen[v] = true; \n q.push(v); \n }\n }\n return ans; \n }; \n \n int ans = 0; \n for (auto& g : group) {\n transform(g.begin(), g.end(), g.begin(), bfs); \n ans += *max_element(g.begin(), g.end()); \n }\n return ans; \n }\n};\n```\n**Python3**\n```\nclass Solution:\n def magnificentSets(self, n: int, edges: List[List[int]]) -> int:\n graph = [[] for _ in range(n)]\n for u, v in edges: \n graph[u-1].append(v-1)\n graph[v-1].append(u-1)\n \n seen = [0]*n\n group = []\n for i in range(n): \n if not seen[i]: \n seen[i] = 1\n stack = [i]\n group.append([i])\n while stack: \n u = stack.pop()\n for v in graph[u]: \n if not seen[v]: \n seen[v] = seen[u] + 1\n stack.append(v)\n group[-1].append(v)\n elif seen[u] & 1 == seen[v] & 1: return -1\n\n def bfs(x): \n """Return the levels starting from x."""\n ans = 0\n seen = {x}\n queue = deque([x])\n while queue: \n ans += 1\n for _ in range(len(queue)): \n u = queue.popleft()\n for v in graph[u]: \n if v not in seen: \n seen.add(v)\n queue.append(v)\n return ans \n \n ans = 0 \n for g in group: ans += max(bfs(x) for x in g)\n return ans \n```\n**Complexity**\nTime `O(N^2)`\nSpace `O(N)`

You are given a positive integer `n` representing the number of nodes in an **undirected** graph. The nodes are labeled from `1` to `n`. You are also given a 2D integer array `edges`, where `edges[i] = [ai, bi]` indicates that there is a **bidirectional** edge between nodes `ai` and `bi`. **Notice** that the given graph may be disconnected. Divide the nodes of the graph into `m` groups (**1-indexed**) such that: * Each node in the graph belongs to exactly one group. * For every pair of nodes in the graph that are connected by an edge `[ai, bi]`, if `ai` belongs to the group with index `x`, and `bi` belongs to the group with index `y`, then `|y - x| = 1`. Return _the maximum number of groups (i.e., maximum_ `m`_) into which you can divide the nodes_. Return `-1` _if it is impossible to group the nodes with the given conditions_. **Example 1:** **Input:** n = 6, edges = \[\[1,2\],\[1,4\],\[1,5\],\[2,6\],\[2,3\],\[4,6\]\] **Output:** 4 **Explanation:** As shown in the image we: - Add node 5 to the first group. - Add node 1 to the second group. - Add nodes 2 and 4 to the third group. - Add nodes 3 and 6 to the fourth group. We can see that every edge is satisfied. It can be shown that that if we create a fifth group and move any node from the third or fourth group to it, at least on of the edges will not be satisfied. **Example 2:** **Input:** n = 3, edges = \[\[1,2\],\[2,3\],\[3,1\]\] **Output:** -1 **Explanation:** If we add node 1 to the first group, node 2 to the second group, and node 3 to the third group to satisfy the first two edges, we can see that the third edge will not be satisfied. It can be shown that no grouping is possible. **Constraints:** * `1 <= n <= 500` * `1 <= edges.length <= 104` * `edges[i].length == 2` * `1 <= ai, bi <= n` * `ai != bi` * There is at most one edge between any pair of vertices.

[Python3] BFS

divide-nodes-into-the-maximum-number-of-groups

**Implementation**\nStep 1: Find all connected components of the graph, this can be achieved by using BFS.\nStep 2: Find the maxinum number of groups in each connected component by using BFS and starting from each node of the component, or `-1` if not valid.\nStep 3: If any of the output from Step 2 is `-1`, then return `-1`; otherwise, return the sum of the output from Step 2 as the final answer.\n\n**Complexity**\nTime Complexity: `O(n*(n+m))`, where `m` is the number of edges\nSpace Complexity: `O(n+m)`\n\n**Solution**\n```\nclass Solution:\n def magnificentSets(self, n: int, edges: List[List[int]]) -> int:\n graph = defaultdict(list)\n for a, b in edges:\n graph[a].append(b)\n graph[b].append(a)\n components = []\n seen = set()\n for i in range(1, n + 1):\n if i in seen:\n continue\n queue = deque([i])\n visited = set([i])\n while queue:\n for _ in range(len(queue)):\n node = queue.popleft()\n for neighbor in graph[node]:\n if neighbor in visited:\n continue\n visited.add(neighbor)\n queue.append(neighbor)\n components.append(visited)\n seen = seen.union(visited)\n longest = [-1] * len(components) \n for k in range(len(components)):\n for i in components[k]:\n longest[k] = max(longest[k], self.bfs(graph, i))\n if min(longest) < 0:\n return -1\n return sum(longest)\n \n def bfs(self, graph, i):\n queue = deque([i])\n seen = set([i])\n seenLevel = set()\n ans = 0\n while queue:\n ans += 1\n nextLevel = set()\n for _ in range(len(queue)):\n node = queue.popleft()\n for neighbor in graph[node]:\n if neighbor in seenLevel:\n return -1\n if neighbor in seen:\n continue\n seen.add(neighbor)\n nextLevel.add(neighbor)\n queue.append(neighbor)\n seenLevel = nextLevel\n return ans\n```

You are given a positive integer `n` representing the number of nodes in an **undirected** graph. The nodes are labeled from `1` to `n`. You are also given a 2D integer array `edges`, where `edges[i] = [ai, bi]` indicates that there is a **bidirectional** edge between nodes `ai` and `bi`. **Notice** that the given graph may be disconnected. Divide the nodes of the graph into `m` groups (**1-indexed**) such that: * Each node in the graph belongs to exactly one group. * For every pair of nodes in the graph that are connected by an edge `[ai, bi]`, if `ai` belongs to the group with index `x`, and `bi` belongs to the group with index `y`, then `|y - x| = 1`. Return _the maximum number of groups (i.e., maximum_ `m`_) into which you can divide the nodes_. Return `-1` _if it is impossible to group the nodes with the given conditions_. **Example 1:** **Input:** n = 6, edges = \[\[1,2\],\[1,4\],\[1,5\],\[2,6\],\[2,3\],\[4,6\]\] **Output:** 4 **Explanation:** As shown in the image we: - Add node 5 to the first group. - Add node 1 to the second group. - Add nodes 2 and 4 to the third group. - Add nodes 3 and 6 to the fourth group. We can see that every edge is satisfied. It can be shown that that if we create a fifth group and move any node from the third or fourth group to it, at least on of the edges will not be satisfied. **Example 2:** **Input:** n = 3, edges = \[\[1,2\],\[2,3\],\[3,1\]\] **Output:** -1 **Explanation:** If we add node 1 to the first group, node 2 to the second group, and node 3 to the third group to satisfy the first two edges, we can see that the third edge will not be satisfied. It can be shown that no grouping is possible. **Constraints:** * `1 <= n <= 500` * `1 <= edges.length <= 104` * `edges[i].length == 2` * `1 <= ai, bi <= n` * `ai != bi` * There is at most one edge between any pair of vertices.

[Python3] Memory Efficient Solution with Detailed Explanation (Easy to Understand)

divide-nodes-into-the-maximum-number-of-groups

# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe graph must be bipartite in order to seperate like this. The proof is not too hard:\n\n1. No cycle: we can separate the graph and it is by definition bipartite.\n2. Cycle with odd length: (suppose we label them 1,2,...,m and start assignment from 1) no matter how we alternate groups, we will find it impossible to get back to the original group for the starting point.\n3. Only cycle with even length: this is by definition bipartite, so we can separate points into 2 groups (black and red). The separation will be constructed interatively as follows: **(a)** starting with a red node and assign it to group 1; **(b)** find all black nodes connected to the red node and assign them to group 2; **(c)** find all red nodes connected to group 2 (but excluding group 1) and assign them to group 3; **(d)** iterate the process and we can get a possible separation.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nObservation:\n1. the construction process in above bullet point 3 can be also applied to bullet point 1. \n2. Based on the construction process, it would be always optimal to use as less points as possible at the beginning. So we always start with just 1 point and iterate all points within the graph to find the max.\n3. We can do the same thing for each connected component.\n\nSo the approach is clear: check bipartite and find the possible max. We can combine these two. The search for connected component is inherent in BFS, so we just need one more hashmap to store the group information.\n\n# Complexity\n- Time complexity: O(V*(V+E)). The repetition of painting nodes still allows some space for optimization.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(V+E)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def magnificentSets(self, n: int, edges: List[List[int]]) -> int:\n graph = defaultdict(list)\n\n for p1,p2 in edges:\n graph[p1].append(p2)\n graph[p2].append(p1)\n\n dist = [0] * (n+1)\n group_dict = {}\n group = 0\n MAX = 0\n\n for i in range(1,n+1):\n # group assignment\n if i not in group_dict:\n group = MAX + 1\n MAX = group\n else:\n group = group_dict[i]\n\n seen = set()\n seen.add(i)\n q = [i]\n level = 0\n\n # color used to check bipartite\n color = [0] * n\n color[i-1] = 1\n c_color = -1\n\n group_dict[i] = group\n\n while q:\n tmp = []\n for p in q:\n for node in graph[p]:\n if color[p-1] * color[node-1] > 0: # check if parent and child can be painted using differen color\n return -1\n if node not in seen:\n seen.add(node)\n tmp.append(node)\n\n group_dict[node] = group # assign to connected component\n color[node-1] = c_color # paint the node\n\n c_color *= -1 # alternate color\n level += 1\n q = tmp\n \n dist[group] = max(dist[group],level) # only corresponding group is updated\n \n return sum(dist)\n \n \n\n \n\n```

You are given a positive integer `n` representing the number of nodes in an **undirected** graph. The nodes are labeled from `1` to `n`. You are also given a 2D integer array `edges`, where `edges[i] = [ai, bi]` indicates that there is a **bidirectional** edge between nodes `ai` and `bi`. **Notice** that the given graph may be disconnected. Divide the nodes of the graph into `m` groups (**1-indexed**) such that: * Each node in the graph belongs to exactly one group. * For every pair of nodes in the graph that are connected by an edge `[ai, bi]`, if `ai` belongs to the group with index `x`, and `bi` belongs to the group with index `y`, then `|y - x| = 1`. Return _the maximum number of groups (i.e., maximum_ `m`_) into which you can divide the nodes_. Return `-1` _if it is impossible to group the nodes with the given conditions_. **Example 1:** **Input:** n = 6, edges = \[\[1,2\],\[1,4\],\[1,5\],\[2,6\],\[2,3\],\[4,6\]\] **Output:** 4 **Explanation:** As shown in the image we: - Add node 5 to the first group. - Add node 1 to the second group. - Add nodes 2 and 4 to the third group. - Add nodes 3 and 6 to the fourth group. We can see that every edge is satisfied. It can be shown that that if we create a fifth group and move any node from the third or fourth group to it, at least on of the edges will not be satisfied. **Example 2:** **Input:** n = 3, edges = \[\[1,2\],\[2,3\],\[3,1\]\] **Output:** -1 **Explanation:** If we add node 1 to the first group, node 2 to the second group, and node 3 to the third group to satisfy the first two edges, we can see that the third edge will not be satisfied. It can be shown that no grouping is possible. **Constraints:** * `1 <= n <= 500` * `1 <= edges.length <= 104` * `edges[i].length == 2` * `1 <= ai, bi <= n` * `ai != bi` * There is at most one edge between any pair of vertices.

Very short just BFS

divide-nodes-into-the-maximum-number-of-groups

# Intuition\nSimilar to other solutions, but just one pass of bfs on each node is sufficient (no odd cycle checking or dsu for finding components).\n\n# Code\n```\nclass Solution:\n def magnificentSets(self, n: int, edges: List[List[int]]) -> int:\n g = defaultdict(set)\n for u,v in edges:\n u, v = u-1, v-1\n g[u].add(v)\n g[v].add(u)\n\n ans = defaultdict(lambda: float(\'-inf\'))\n for u in range(n):\n q, visited, steps = [u], set([u]), 0\n while q:\n steps += 1\n q1 = set()\n for u in q:\n for v in g[u]:\n if v in q: return -1\n if v not in visited:\n q1.add(v)\n visited.add(v)\n q = q1\n \n k = min(visited)\n ans[k] = max(ans[k], steps)\n\n return sum(ans.values())\n```

You are given a positive integer `n` representing the number of nodes in an **undirected** graph. The nodes are labeled from `1` to `n`. You are also given a 2D integer array `edges`, where `edges[i] = [ai, bi]` indicates that there is a **bidirectional** edge between nodes `ai` and `bi`. **Notice** that the given graph may be disconnected. Divide the nodes of the graph into `m` groups (**1-indexed**) such that: * Each node in the graph belongs to exactly one group. * For every pair of nodes in the graph that are connected by an edge `[ai, bi]`, if `ai` belongs to the group with index `x`, and `bi` belongs to the group with index `y`, then `|y - x| = 1`. Return _the maximum number of groups (i.e., maximum_ `m`_) into which you can divide the nodes_. Return `-1` _if it is impossible to group the nodes with the given conditions_. **Example 1:** **Input:** n = 6, edges = \[\[1,2\],\[1,4\],\[1,5\],\[2,6\],\[2,3\],\[4,6\]\] **Output:** 4 **Explanation:** As shown in the image we: - Add node 5 to the first group. - Add node 1 to the second group. - Add nodes 2 and 4 to the third group. - Add nodes 3 and 6 to the fourth group. We can see that every edge is satisfied. It can be shown that that if we create a fifth group and move any node from the third or fourth group to it, at least on of the edges will not be satisfied. **Example 2:** **Input:** n = 3, edges = \[\[1,2\],\[2,3\],\[3,1\]\] **Output:** -1 **Explanation:** If we add node 1 to the first group, node 2 to the second group, and node 3 to the third group to satisfy the first two edges, we can see that the third edge will not be satisfied. It can be shown that no grouping is possible. **Constraints:** * `1 <= n <= 500` * `1 <= edges.length <= 104` * `edges[i].length == 2` * `1 <= ai, bi <= n` * `ai != bi` * There is at most one edge between any pair of vertices.

Python solution | DFS + BFS (beats 100 % of the users)

divide-nodes-into-the-maximum-number-of-groups

# Code\n```\nfrom collections import deque\n\nclass Solution:\n def magnificentSets(self, n: int, edges: List[List[int]]) -> int:\n graph = [[] for _ in range(n)]\n for u, v in edges:\n graph[u - 1].append(v - 1)\n graph[v - 1].append(u - 1)\n\n seen = [0] * n\n groups = []\n\n # DFS to assign and validate groups\n for i in range(n):\n if not seen[i]:\n seen[i] = 1\n stack = [i]\n component = [i]\n while stack:\n u = stack.pop()\n for v in graph[u]:\n if not seen[v]:\n seen[v] = seen[u] + 1\n stack.append(v)\n component.append(v)\n elif (seen[u] & 1) == (seen[v] & 1):\n return -1\n groups.append(component)\n\n # BFS function to find maximum number of groups from a node\n def bfs(x):\n ans = 0\n seen = [False] * n\n seen[x] = True\n q = deque([x])\n while q:\n ans += 1\n for _ in range(len(q)):\n u = q.popleft()\n for v in graph[u]:\n if not seen[v]:\n seen[v] = True\n q.append(v)\n return ans\n\n # Apply BFS to all nodes in each connected component\n ans = 0\n for group in groups:\n group = [bfs(x) for x in group]\n ans += max(group)\n\n return ans\n\n\n```

You are given a positive integer `n` representing the number of nodes in an **undirected** graph. The nodes are labeled from `1` to `n`. You are also given a 2D integer array `edges`, where `edges[i] = [ai, bi]` indicates that there is a **bidirectional** edge between nodes `ai` and `bi`. **Notice** that the given graph may be disconnected. Divide the nodes of the graph into `m` groups (**1-indexed**) such that: * Each node in the graph belongs to exactly one group. * For every pair of nodes in the graph that are connected by an edge `[ai, bi]`, if `ai` belongs to the group with index `x`, and `bi` belongs to the group with index `y`, then `|y - x| = 1`. Return _the maximum number of groups (i.e., maximum_ `m`_) into which you can divide the nodes_. Return `-1` _if it is impossible to group the nodes with the given conditions_. **Example 1:** **Input:** n = 6, edges = \[\[1,2\],\[1,4\],\[1,5\],\[2,6\],\[2,3\],\[4,6\]\] **Output:** 4 **Explanation:** As shown in the image we: - Add node 5 to the first group. - Add node 1 to the second group. - Add nodes 2 and 4 to the third group. - Add nodes 3 and 6 to the fourth group. We can see that every edge is satisfied. It can be shown that that if we create a fifth group and move any node from the third or fourth group to it, at least on of the edges will not be satisfied. **Example 2:** **Input:** n = 3, edges = \[\[1,2\],\[2,3\],\[3,1\]\] **Output:** -1 **Explanation:** If we add node 1 to the first group, node 2 to the second group, and node 3 to the third group to satisfy the first two edges, we can see that the third edge will not be satisfied. It can be shown that no grouping is possible. **Constraints:** * `1 <= n <= 500` * `1 <= edges.length <= 104` * `edges[i].length == 2` * `1 <= ai, bi <= n` * `ai != bi` * There is at most one edge between any pair of vertices.